基于灰色模型与三次样条插值的预测研究

杨程　郑兰香　李春光

摘要：选择灰色模型和三次样条插值相结合，对3个不同领域的非等时距数据样本进行了预测。结果表明，该算法能够较为准确地对非等时距样本进行预测，且简单易行，预测值精度高于文献算法。在工程实际中，该算法更加实用，并能够应用于多种工程领域。

关键词：非等时距；灰色模型；三次样条插值；模型精度

中图分类号：TU12 文献标识码：A 文章编号：0439-8114（2015）22-5729-03

Abstract： A combination forecasting algorithm based on gray model and cubic spline interpolation was proposed.Using this method to predict the data samples from non-isochronous， they belong to three different fields. The results show that： the proposed algorithm can more accurately predict the samples from non-equal interval， and simple， the accuracy of the predicted values are also higher than the literature. In the project， the proposed algorithm is more practical， and can be used in a variety of engineering fields.

Key words： non-equal interval； gray model； cubic spline interpolation； accuracy of the model

20世纪80年代，邓聚龙提出灰色系统理论，该理论是一种研究少数据、贫信息和不确定性问题的新方法[1]，已被广泛应用于工程控制、社会生态、管理、农业等领域的评价中。经典的GM（1，1）模型是以等时距序列为基础的，但在实际中，监测得到的样本是非等时距的。在利用灰色模型对其进行预测研究时，主要有两种思路：①对灰色模型进行改进，构造非等时距的灰色模型[2-7]；②采用插值方法对非等时距样本进行处理，然后利用灰色模型进行预测研究。本研究选择三次样条插值算法与非等时距灰色模型结合，对非等时距样本进行预测，并与实测值和文献采用的方法进行对比分析。

1 数学模型

1.1 采用三次样条插值算法处理原始样本

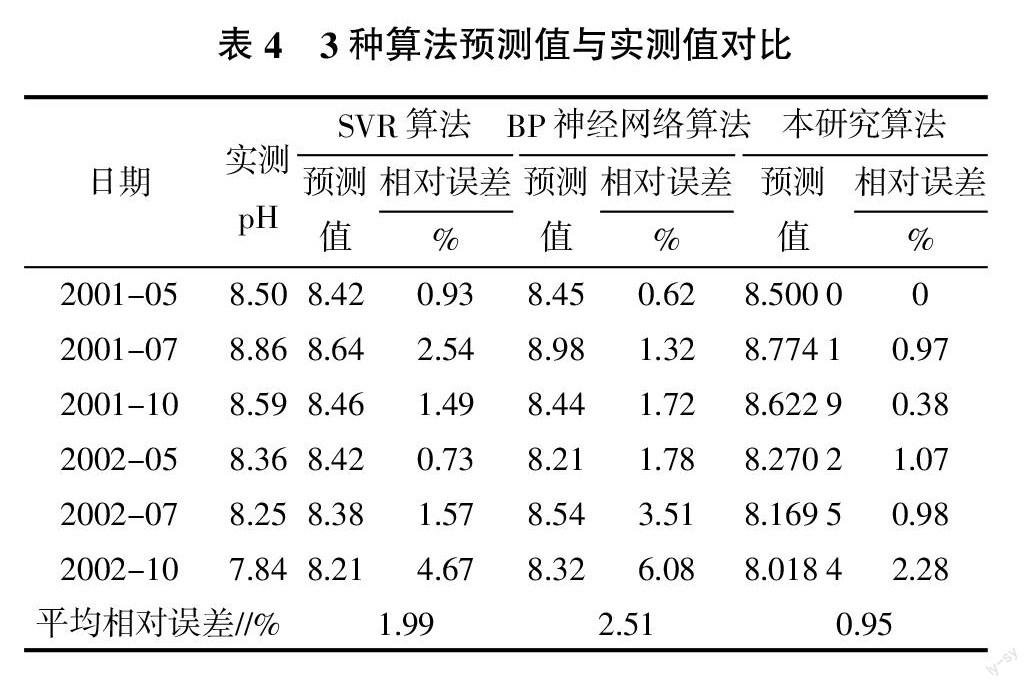
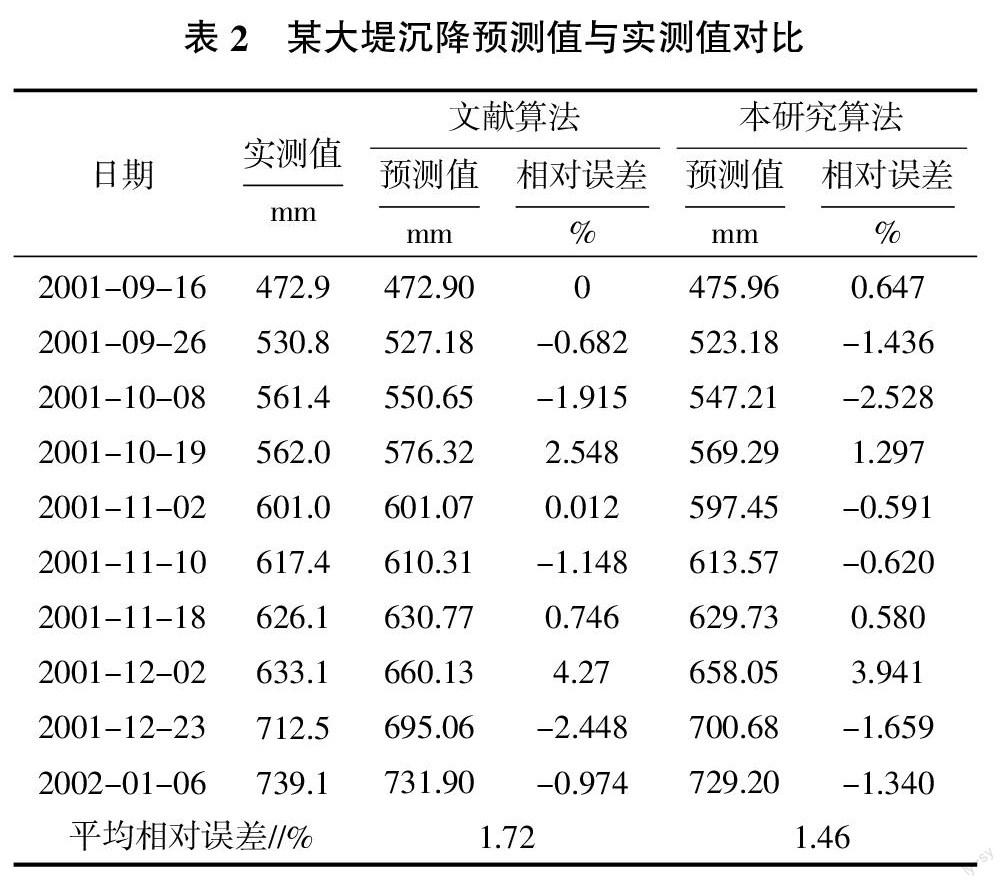
样条插值可以使用低阶多项式，避免了使用高阶多项式所出现的龙格现象。三次样条插值（简称Spline插值）是通过一系列形值点的一条光滑曲线，在数学上是通过求解三弯矩方程组得出曲线函数组的过程。三次样条插值具有二阶光滑度，在工程上应用比较广泛。其具体定义如下：函数S（x）∈C2[a，b]，在每个小区间[xj，xj+1]是三次多项式，其中a=x0

采用三次样条插值算法，对非等时距样本进行处理即选择合适的时间间隔，采用三次样条插值算法，将原始样本处理为等时距的样本。由于该算法的收敛性和误差估计有着严格的理论依据，故将处理后的样本作为新的原始样本而产生的误差，对预测计算精度的影响是可控的。

1.2 级比检验

1.3 GM（1，1）建模

模型精度p越大预测精度越高，后验差比值C越小预测误差的离散型越小。一般根据p和C，将预测精度分为4级，如表1所示。

3 实例验证

3.1 实例一

文献[5]对某防洪大堤施工阶段部分沉降数据进行了预测。本研究利用该数据，采用文中提出的简单组合算法进行预测，并与文献算法结果进行对比分析，结果如表2所示。

由表2可知，与文献算法预测值相比，本研究算法的模型精度为0.985 4，后残差比值为0.000 3。该模型精度为1级，并且预测值的平均相对误差也较小。

3.2 实例二

文献[7]构造非等时距加权灰色模型与神经网络组合算法，对轨道不平顺进行预测研究。根据文献实测数据，采用本研究算法对其预测，与实测值和文献[7]预测结果进行对比分析，结果如表3所示。

由表3可知，与文献算法预测值相比，本研究算法的模型精度为0.983，后残差比值为0.147 4。该模型精度为1级，并且预测值的平均相对误差也较小。

3.3 实例三

文献[10]采用4种算法进行预测、对比，其中支持向量回归机（SVR）算法的模拟、预测精度最高，其次是BP神经网络算法。采用本研究构造的算法对样本进行模拟，并将预测值与文献[10]中两种算法的预测值进行对比，结果如表4所示。

由表4可知，本研究算法计算的平均相对误差最小。SVR算法的预测值的p=0.98，C=0.0918；BP算法的预测值的p=0.97，C=0.1019；本研究算法的预测值的p=0.99，C=0.0492。该模型精度为1级。

4 小结

对工程中采用非等时距样本进行高效的预测是非常重要的。本研究对其预测的数学模型进行了研究，考虑到工程中需要简单易行、精度高的算法，提出基于传统灰色模型和三次样条插值的组合算法，对3个不同领域的非等时距的数据样本进行预测，并将结果与实测值和文献算法得到的预测值进行对比分析。结果表明，本研究提出的组合算法简单易行，模型精度为1级，算法预测值的精度高于文献中的算法。故对于工程而言，本研究算法更实用，且能应用于多种领域。

参考文献：

[1] 陈 榕，钟林志，赵 超，等.基于改进灰色模型的建筑能耗预测研究[J].福州大学学报（自然科学版），2013，41（5）：903-908.

[2] 刘金英.灰色预测理论与评价方法在水环境中的应用研究[D].长春：吉林大学，2004.

[3] 曲建军，高 亮，张新奎，等.基于灰色GM（1，1）非等时距修正模型的轨道质量预测[J].中国铁道科学，2009，30（3）：5-8.

[4] 曾祥艳，曾 玲.非等间距GM（1，1）模型的改进与应用[J].数学的实践与认知，2011，41（2）：90-95.

[5] 韓 晋，杨 岳，陈 峰，等.基于非等时距加权灰色模型与神经网络的组合预测算法[J].应用数学和力学，2013，34（4）：408-419.

[6] 曾鼎文，吴浩中.优化的非等时距灰色模型在湖南高速公路路基沉降预测中的应用[J].公路工程，2013，38（4）：269-272.

[7] 韩 晋，杨 岳，陈 峰，等.基于非等时距加权灰色模型与神经网络的轨道不平顺预测[J].铁道学报，2014，36（1）：81-87.

[8] 曹 彦，谭永杰，周 驰.灰色模型和最小二乘支持向量机在短期负荷组合预测中的应用[J].许昌学院学报，2013，32（5）：32-37.

[9] 孙丽军，杨家冕.非等时距灰色模型在地压灾害预测研究中的应用[J].金属矿山，2011（10）：51-54.

[10] 武国正.支持向量机在湖泊富营养化评价及水质预测中的应用研究[D].呼和浩特：内蒙古农业大学，2008.

（责任编辑 屠 晶）