尺寸精度的灰色预测模型研究
韩兴国 崔学峰
摘要:在工件加工过程中影响尺寸精度的因素很多,有些因素是随机的、无规律的,是一个灰色量,因此文章通过建立GM(1,1)模型对尺寸精度进行预报。而考虑到外界因素对系统的扰动,使得数据存在失真的可能,以此引进缓冲算子的概念,与原始数据建立的模型的预测值进行比较,判断是否存在数据失真的可能,保证预报精度。
关键词:尺寸精度;灰色模型;缓冲算子
1 引言
机械产品加工过程中影响尺寸精度的因素很多,其中的主要影响因素:原始误差,机床误差,刀具误差是没办法测量的,所以机械加工过程是个典型的灰色过程。
灰色模型就是应用数理统计知识和建模理论,根据已知的少量信息进行建模,减弱系统的随机性。由于随时间变化的因素太多,使得机械加工尺寸有时变性。要想机械加工尺寸有较为准确的预报,就需要模型能考虑外界环境对尺寸加工的影响,使得模型能对加工系统及时做出正确的反应。在传统灰色模型的基础上,通过指数型弱化算子的构造弱化外界环境对原始数据失真的干扰,以此优化预报模型的预报精度。
2 GM(1,1)模型的建立
灰色预报模型主要是通过先建立原始序列,对原始序列进行一次累加生成累加序列,通过最小二乘法求出参数的计算公式,以微分方程作为演绎推理工具等,得到时间响应序列函数,然后对模型进行理论和实验分析,对尺寸精度进行灰色预报。
2.1 试验准备
试验时使用的车床为C5112A型数控单住立式车床,内圆直径尺寸为mm的进油环,通过实验观察在连续加工过程中车削加工的尺寸偏差的趋势性和随机性,发现机械加工过程对加工尺寸的影响规律。
2.2 试验数据
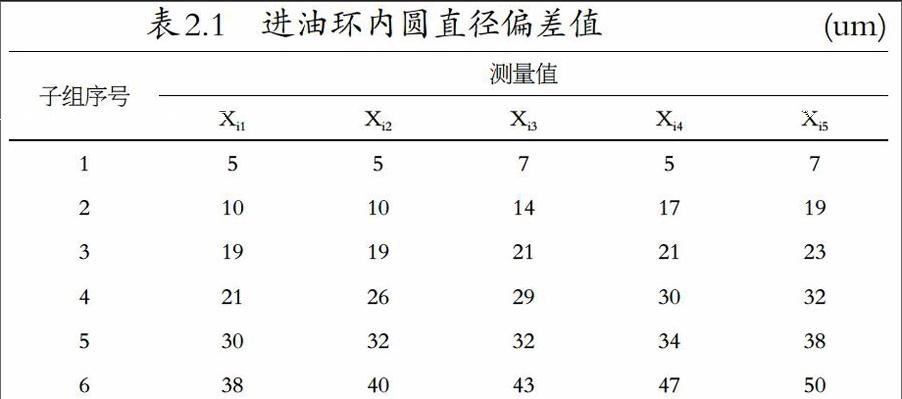
取直径尺寸偏差为预报对象,以进油环内圆直径尺寸的偏差值为建模的序列,建立GM(1,1)模型。偏差值见表2.1
2.3 试验过程
试验步骤如下:
第一步建立原始序列。将表2.1中的原始数据以6个为单位代入时间序列GM(1,11模型,设进油环内圆直径尺寸变量X(0)={X(0)(i),i=1,2,…,n}。
第二步建立累加序列。对X(0)进行一次累加生成一次累加序列:X(1)={X(1)(K),K=1,2,…,n}=(5 10 19 21 30 38}
第三步生成微分方程。GM(1,1)模型相应的微分方程为
+ax(1)=μ (式2.1)
式中:a为发展灰数;μ为内生控制灰数。
第四步利用最小二乘法求解。即可得预测模型
+1)=37.43.14 (式2.4)
用式2.4即可算出预测值如表2.2所示
3 精度优化
引入缓冲算子,优化模型精度。首先对原始数据序列进行一阶弱化处理,建立基于弱化缓冲算子处理后数据序列的生成模型,将生成模型还原成原始数据模型进行预测从而起到弱化数据失真的作用,优化模型预测精度。
3.1 指数型弱化缓冲算子的构造
基本概念:设X(0)=(X(0)(1),X(0)(2),……,X(0)(n))为系统真实行为序列,而观察到的系统行为数据序列为X=X(0)(1)+ε1,X(0)(2)+ε2,
……,X(0)(n)+εn=X(0)+ε,其中ε=(ε1,ε2,……,εn)是n个冲击扰动组成的数据序列,称x为冲击扰动序列。
弱化缓冲算子序列的构造:设为系统行为特征序列,且令缓冲序列XD1=(x(1)d1,x(2)d2,……,x(n)d1),
x(k)d1)
则当X为单调序列(不论增长或衰减)或振荡序列时,D1、D2、D3、D4皆为弱化缓冲算子。
对原始数据序列x=(5 10 19 21 30 38),利用一阶k次平均弱化缓冲算子,将原始数据进行一阶弱化处理,处理后利用GM(1,1)模型分别对缓冲作用序列建模。经缓冲算子D1、D2、D3、D4作用后的弱化缓冲序列分别为XD1、XD2、XD3、XD4,相应的分别建立GM(1,1)模型,可得预测模型为:
+1)=35.43.15
+1)=32.13.05
+1)=30.73.12
+1)=31.63.13
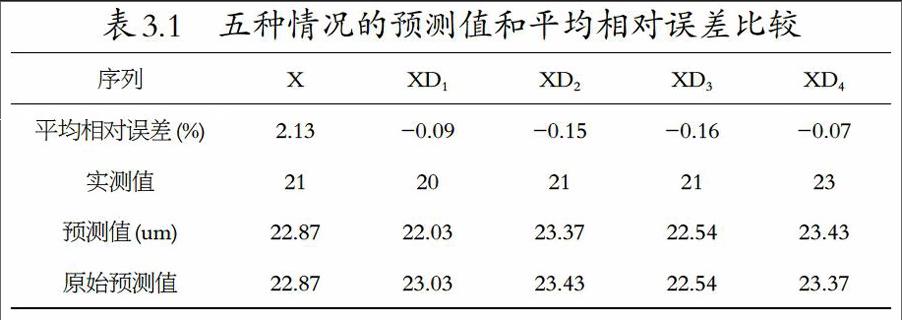
通过模型所得预测值与原始数据建立的模型所得预测值的相对误差如表3.1:
从图中数据可以看出,预测值相对误差比较小,表明外界扰动因素对原始数据失真的影响较小,预测模型对精度反应准确,同时,说明在模型预测中可以引入缓冲算子,当数据存在失真状态时,修正模型精度。
4 结论
4.1 运用灰色预测模型,对改进后的生产过程进行预测。灰色预测模型能考虑外界环境对尺寸加工的影响,使得模型能对加工系统及时做出正确的反应。
4.2 引入弱化缓冲算子,优化模型精度。通过试验建立的模型可以用来预测尺寸精度,减少生产过程中的调试次数,但加工过程中对工件的影响因素具有时变形和动态性,一些数据序列的波动差异性比较显著,为了建模后得到的模拟误差相对较小,引入弱化缓冲算子,优化模型预测精度。