古塔形变问题的数学模型

屈 哲，郭 辉

(青岛滨海学院大专理科基础学院，山东青岛 266555)

1 古塔各层中心位置的测定方法

1.1 确定任意凸多边形重心

做凸四边形的一条对角线，就将四边形分为两个三角形，分别作两个三角形的重心为A和B，连接A、B得一线段AB。同样，做出凸四边形的另一条对角线，用相同的办法得到线段CD，AB和CD的交点就是凸四边形的重心［1］，如图1所示。

图1 凸四边形的重心

做凸五边形的任一条对角线，将凸五边形分为一个三角形与一个四边形组合体，分别作出三角形的重心和四边形的重心，并连成线段AB;做五边形的另外一条对角形，将五边形分为另一个三角形与四边形的组合体，分别作出三角形与四边形的重心，并连接成线段CD;则AB和CD的交点就是五边形的重心，如图2所示。

图2 凸五边形的重心

一条对角线，将N边形化为一个三角形与(N－1)边形，或四边形与(N－2)边形，然后分别作出重心，并连接成线段，然后再连接另一条对角线，分别作出两个组合体的重心并连接成线段，两条线段的交点就是N边形的重心。

1.2 任意凸多边形重心的算法

基于上述理论，运用VC++得出确定一个任意凸多边形重心的通用方法，具体算法及程序如下［2－3］:

(1)在平面上取一点(一般取原点)得到N个三角形 OP［i］P［i+1］，其中点的顺序为逆时针。

(2)分别求出这N个三角形的重心Ci和面积Ai，注意此处面积是有向面积，用叉乘求面积时应保留其正负号。

(3)求出A=A1+A2+…+AN(同样保留正负号的代数相加)。

(4)重心C=sigma(Ai+Ci)/A。

2 古塔倾斜、弯曲、扭曲的形变数学模型

2.1 古塔的倾斜分析

建筑物的倾斜，即其主体的中心轴线偏离铅垂线且与铅垂线有一个夹角，古塔是一座八边形的建筑物，为了研究方便，可将塔体简化为锥体，如图3所示。塔体倾斜在竖面上的反映是:塔的中心轴线偏离铅垂线，其偏离角度为 θ［4］。

图3 塔体简化为锥体

设古塔塔顶的顶点坐标为A(x14，y14，z14)，第一层塔的中心坐标为B(x1，y1，z1)，连线AB即是古塔中心轴线，利用空间向量对两点的坐标做差得出x1，y14－y1，z14－ z1}，利用空间向量方向角的余弦公式

根据上述仿真数据，得到4年古塔的倾斜角数据如表1所示。

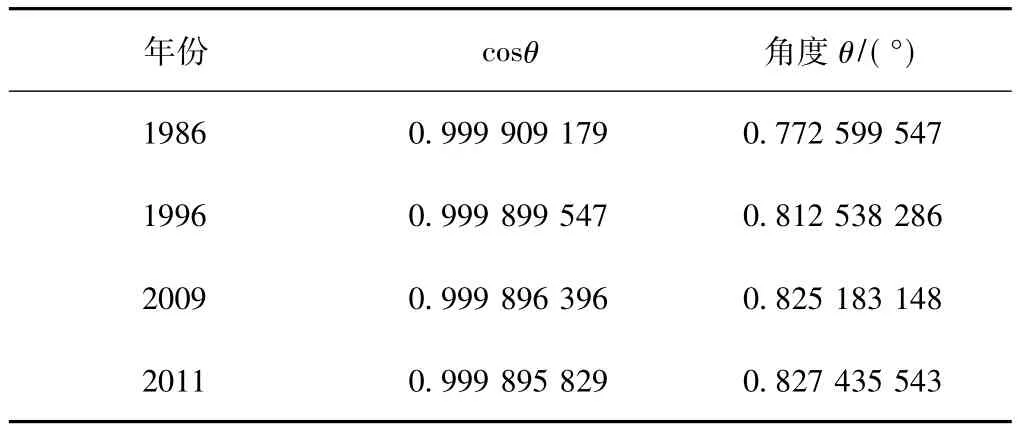
表1 古塔的倾斜角

由表1的数据可观察到θ随时间逐渐变大，说明塔的中心轴线与铅垂线之间的偏离角度θ在不断变大，塔随着年份的增加倾斜度逐渐增大。但在1996～2011年的15年间倾斜角度增大的趋势逐渐变缓。

2.2 古塔的扭曲分析

物体因外力作用而发生的扭转形变叫做物体的扭曲。古塔的扭曲即是古塔在受到外力的作用下中心轴假设不动，塔身相邻两段向相反两个方向的扭转叫扭曲形变。

在古塔的观测数据中每一层都有8个被观测点，为研究分析古塔的扭曲形变，需要选取其中一个被观测点作为研究的被观测点，假设古塔没有发生竖直方向上的形变(例如沉降)，不考虑z轴的变化，每一层均作为一个研究平面，只考虑x，y轴上坐标的变化，用最后一次对这一固定点的观测(2011年)数据与第一次观测(1986年)的数据做差，得到25年来每一层这一固定点的累计变化量。

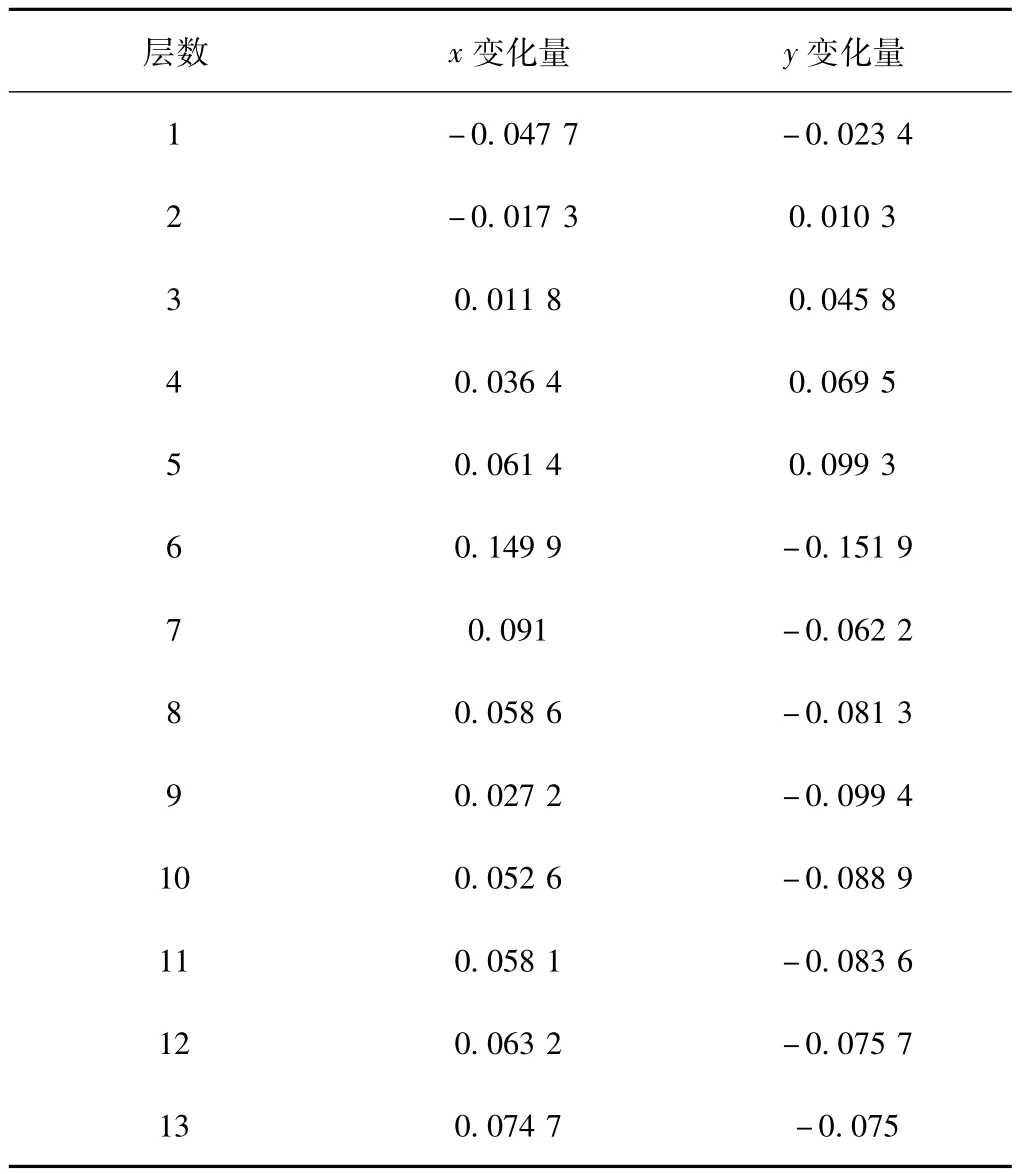
表2 古塔每层固定点的累计变化量

由表2中可知x，y轴坐标的变化发生在不同的方向上，即该固定点在这25年以来塔身2～5层与1层和6～13层扭转的方向不一致，所以古塔由于受到外力的影响而发生了扭转的形变，即古塔发生了扭曲形变。

2.3 古塔的弯曲分析

当物体受到与物体轴线垂直的外力或在轴线平面内的力偶作用时，物体的轴线由原来的直线变成曲线，这种形变称作弯曲形变。为了研究方便且保持结果的准确性，建立如图4所示平面直角坐标系，并以此确定古塔每一层的8个方位。

图4 古塔的弯曲形变示意图

研究古塔的弯曲形变即:研究古塔各层重心与空间直角坐标系的坐标原点的连线形成的向量轴所成的方向角，由空解析几何原理计算如下

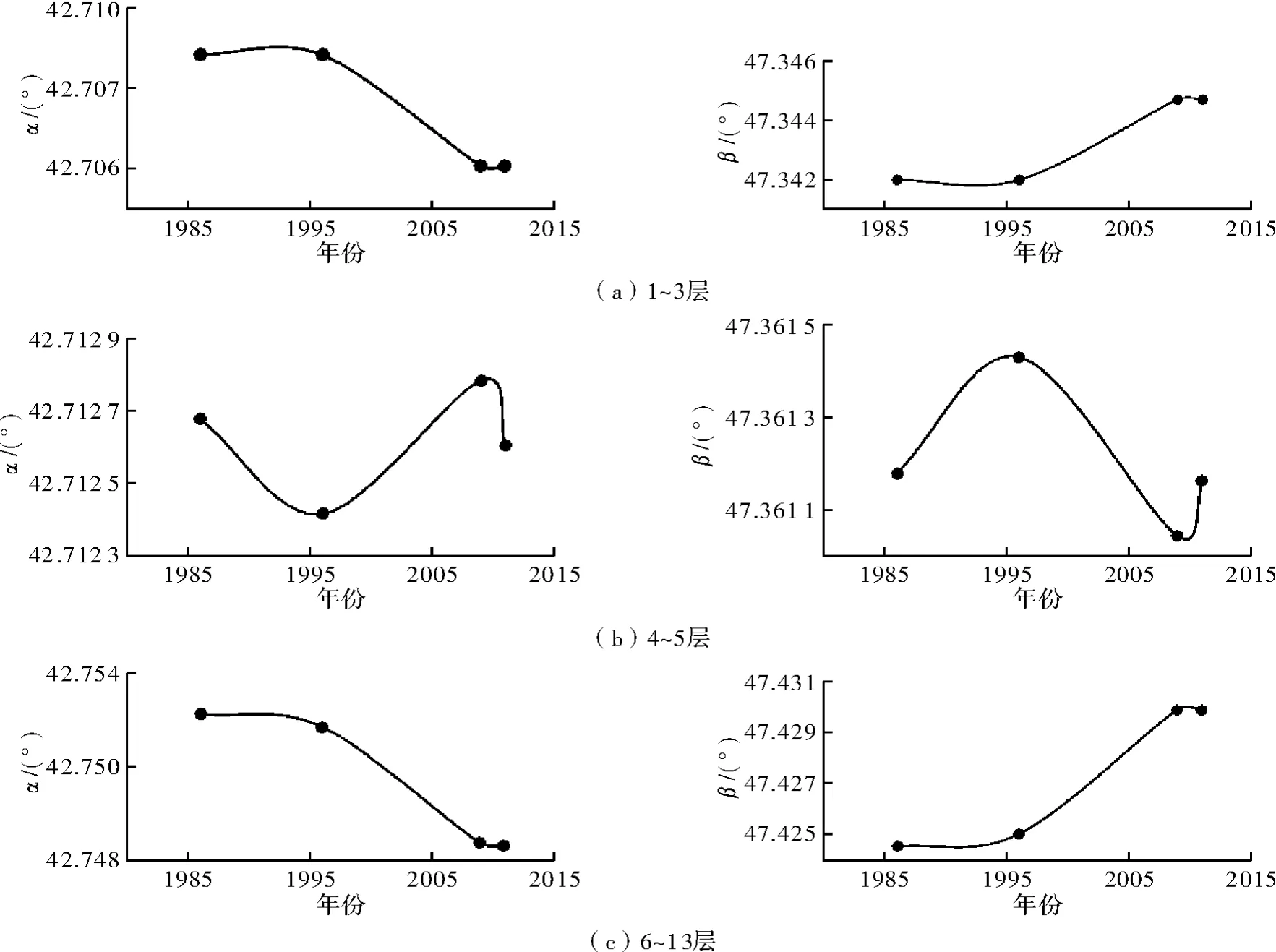
图5 古塔弯曲形变分析

由图5可知:1～3层从1986年～2011年向东南方向倾斜;4～5层1986年～1996年先向东南方向倾斜，1996年～2009年向西北方向倾斜，2009年～2011年向东南方向倾斜;6～13层1996年～2011年向东南方向倾斜。

3 古塔的形变趋势

3.1 古塔的倾斜形变趋势分析

根据上述的研究结果，利用最小二乘法可将古塔形变的趋势拟合成一条光滑曲线，同时还可得出拟合曲线的多项式方程，以此来定量分析该古塔的形变趋势，得出古塔倾斜趋势二次多项式为

3.2 古塔扭曲、弯曲形变的趋势分析

在实际工程中，建筑物扭曲和弯曲一般是同时发生的，这是因为建筑物受到横向和纵向的不可抗力作用而发生的形变。本文研究了古塔身各层扭曲和弯曲的情况，根据研究发现古塔第5层弯曲、扭曲方向与其上面的各层不一致，这是因为该层是塔身的受力中心。因此通过研究该层的重心，即可得出整个古塔的扭曲和弯曲的形变趋势。拟合得出古塔扭曲趋势的二次多项式函数

4 结束语

定量分析了古塔受到外界自然环境的影响产生倾斜、弯曲和扭曲等形变情况及形变趋势的预测问题。分析发现:古塔随着年份的增加倾斜度逐渐增大。但倾斜角度增大的趋势逐渐变缓;同时分析发现古塔存在一定程序的扭曲现象，但扭曲程度不大;同时，古塔也存在一定程度的弯曲现象，弯曲趋势的也在逐渐变缓。通过建立数学模型定量分析研究古塔的形变趋势，为文物部门及时准确了解古塔随时间增加而发生的形变趋势，加强对古塔的维修，制定及时、科学的保护措施提供了理论依据。

［1］ 李涛，贺勇军．应用数学篇［M］．北京:电子工业出版社，2000．

［2］ 姜启源，谢金星．数学建模［M］．北京:高等教育出版社，2003．

［3］ 钱能．C程序设计语言［M］．北京:机械工业出版社，2002．

［4］ 彭明．建筑结构［M］．郑州:黄河水利出版社，2009．

［5］ 袁新生，邵大宏，郁时炼．Lingo和Excel在数学建模中的应用［M］．北京:科学出版社，2006．

［6］ 匡松．Excel电子表格［M］．北京:中国铁道出版社，2009．

［7］ 陈彦萍，田改玲，张建科．基于调节熵函数的Web服务组合算法［J］．西安邮电大学学报，2013(4):64－70．

［8］ 马进．数字预失真基本原理［J］．电子科技，2006(9):17－21．