无标度网络的局部搜索策略

曾 成，孙雅倩，徐玉珠，张达敏

(贵州大学大数据与信息工程学院，贵州贵阳 550025)

复杂网络搜索中较为经典的算法有基于随机游走(Random Walk，RW)搜索策略和最大度(High Degree Seeking，DS)搜索策略［1－3］。文献［4］研究出了一种新的搜索策略，即最大－最小度搜索(Max－Min degree seareh，MM)策略，此策略高效地改良和扩充了最大度搜索策略，将网络中的所有节点根据其度的大小分成两块，一块是最大度效果占优的节点，其会选择最大度搜索策略，而其余节点就会选择MM搜索策略。此策略可根据网络中度的分布改变其系数来完成从最大度到随机游走的变换，因此在无标度网络中较为高效。此策略虽优，但其却并未考虑复杂网络中有着的小世界性质，也忽略了其他表现网络特性的参数，如常见的聚类系数和最小距离等。

本文借鉴文献［4］的思路，引入了聚类系数和最小距离，结合了最小聚类系数搜索策略和贪婪算法，提出一种高效的局部搜索策略，旨在BA无标度网络上有更好的搜索效果。

1 理论分析

因聚类系数小的节点有更高的度，且其邻居节点之间有连接的概率也较小，所以在小世界网络上最小聚类系数搜索策略比最大度搜索策略的性能要好。在小世界网络中，短程所连接的两个节点的邻居节点之间有连边的概率较大，因此，度大的节点并不意味着聚类系数就小。但长程所连接的两个节点的邻居节点之间有连边的概率较小。因此，含有长程连接且度大的节点聚类系数较小［5－7］。总之，点的聚类系数越高就意味着其邻居节点之间有连接的可能性越大，即此节点有更高的重要性。聚类系数的计算公式为

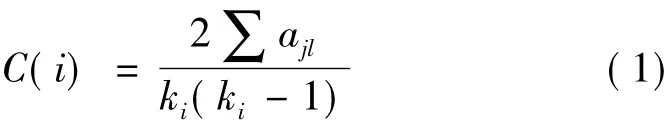
这里ki是节点i的度，节点j和节点l是节点i的邻居节点，ajl是节点i的邻居节点之间实际存在的边数。例如ajl=1表示节点i的邻居节点j和l之间有一条边相连;ajl=0表示节点i的邻居节点之间j和l之间没有边相连。图1是网络中节点的聚类系数分布的示意图。

图1 网络中节点聚类系数的分布

从图中可发现，节点C的聚类系数最小，但其确是此网络的局部中心节点，其他聚类系数大的节点均是网络的局部边缘节点。例如，聚类系数最大的节点(A、B、D、E、J、G、F、H、I)均是网络的边缘节点。所以，可得出结论:节点的聚类系数和重要性成反比，即聚类系数越小，重要性越高;换句话说，聚类系数越小的节点就越容易成为网络的局部中心节点，聚类系数越大的节点就越有可能成为网络的局部边缘节点。

网络中一个最简单基本的搜索策略就是贪婪算法。定义di为当前节点的邻居节点i到目的节点的距离，如图2所示。定义ki为当前节点的邻居节点i的度。贪婪算法选择di最小的邻居节点。这样离目标节点最近的点便更加有可能接收信息［8］。尽管如此，贪婪算法在度分布不均匀的无标度空间网络上并非是最优的搜索策略。文献［9～10］指出利用网络的非均匀特性设计出的算法优于不利用该特性设计出的算法。确实，选择一个聚类系数较小的邻居节点，即使该节点离目标节点很远，但该节点存在长程连接的概率仍较大，在下一次传递信息时，可将信息沿着长程连接传递，接收到信息的节点有可能离目标节点较近。例如，在图3中，源节点将信息传递给节点2比节点1要好，因节点2有一个长程连接，信息传递给节点2后该节点将信息沿着长程连接传递，则节点4就可以收到信息［11］。

图2 贪婪算法节点搜索图

图3 最小聚类系数节点搜索图

从图3中可看到，节点4比节点1的邻居节点离目标节点更近。定义网络中两个节点u和v之间的距离d(u，v)为两节点之间的欧几里得距离，设u的坐标为(i，j)，v的坐标为(k，i)，则有

通过上述分析可知，若选择一个聚类系数较小的邻居节点，则该节点存在长程连接的概率较大，便有可能更快地找到目标节点。因此，可思考在无标度空间网络上结合贪婪算法和最小聚类系数搜索策略的优点，将信息传递给聚类系数较小且离目标节点较近的邻居节点，从而快速地找到目标节点［12－13］。

2 最小聚类系数最短距离搜索算法

既然节点的聚类系数用ci表示，节点到目的节点的距离用di表示，则文中可将这两个量结合到一起，用ci×di便可设计出最小聚类系数最小距离搜索策略。该搜索策略在传递信息的每一步将信息传递给ci×di最小的邻居节点，则就可将信息传递给聚类系数较小且离目标节点较近的邻居节点。这种搜索策略在寻找两个节点之间的路径步骤如下:

步骤1 开始选取目标节点t和源节点s，且将源节点s作为当前节点。

步骤2 从当前节点s开始，查询当前节点s的邻居节点是否有目标节点t。若没有目标节点t，则当前节点选择ci×di最小的节点为当前节点;若有目标节点t，则搜索终止。

步骤3 每一个节点只能被访问一次，若某一节点被访问两次，则搜索失败。

步骤4 重复步骤2和步骤3，直到当前节点为目标节点的任一个邻居节点为止。

该搜索策略是最大度搜索策略和贪婪算法的结合，该搜索算法在传递信息给邻居节点时，不仅考虑邻居节点的度，且还要考虑邻居节点到目的节点的距离本文的目的是要设计一个在无标度空间网络模型上搜索效率高的分散式搜索算法。该算法利用网络的局部信息来将信息从源节点s沿着网络中旳边传递到目的节点t。每一个节点均已知目的节点的位置信息、邻居节点的位置信息和邻居节点的度。利用这些信息、源节点和收到信息的每一个节点，根据搜索策略，将信息传递给其的邻居节点，直到信息到达目的节点为止。

3 仿真结果

为了不失一般性选择由Barabasi与Albert提出的B－A模型作为网络基本构造，模型产生方法与文献［14］相同，其节点的度分布p(k)具有幂律特性，即p(k) ～k－γ，γ =3，k为节点度，γ 为幂律指数。

建立网络模型后，文中随机选择500对节点作为源节点和目的节点来模拟搜索策略。源节点和每一个收到信息的节点均按照不同的搜索策略将消息传递给自身的邻居节点。当信息传递到目标节点的任何一个邻居节点时，搜索过程结束。为了避免信息传递给已收到过信息的邻居节点，文中采取的方法是当节点收到信息时，将该节点做一个访问标记。若一个节点被访问过两次，则该搜索过程失败。为了分析和比较各搜索策略的搜索性能，对每一种搜索策略，统计其平均路径长度、成功率、平均搜索时间、网络覆盖时间、步数和访问节点数关系的不同搜索性能。比较了不同的搜索策略在网络规模为5 000时的搜索性能的优劣程度。

图4是搜索步数与累积访问节点个数之间的关系图。可以看出，在最初的50步中最小聚类系数算法已覆盖了网络中近65%的节点，优于最小聚类系数最小距离算法。但随着步数的增加，后者覆盖效果逐渐变好，达到全网络覆盖比最大度算法少了近2 000步。

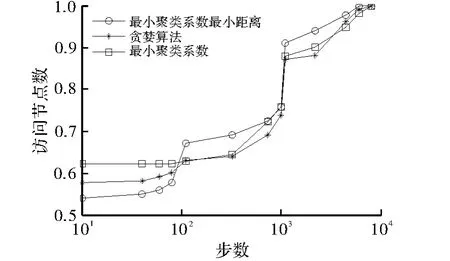
图4 使用3种算法步数与访问节点数的关系

图5所示是随着网络规模的增大，所有搜索策略的平均路径长度均变长，且最小聚类系数最小距离搜索策略的平均路径长度要比最小聚类系数和随机游走及贪婪算法的要短。但当网络规模增加到一定程度时，最小聚类系数搜索策略的平均路径长度要比随机游走搜索策略的长，这是因为随机搜索策略的成功率低。

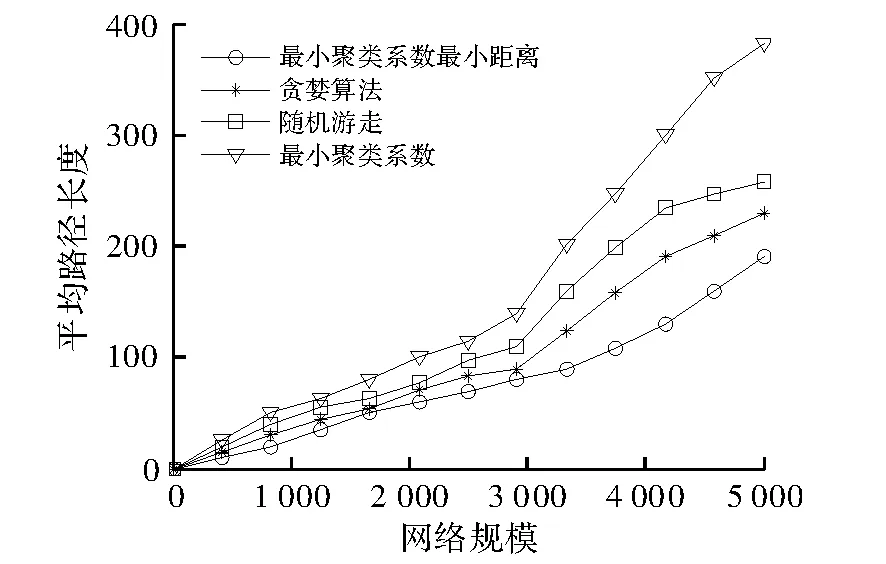
图5 相对路径长度与网络规模的关系

通过图6可发现，随着网络规模的增大，最小聚类系数最小距离搜索策略的成功率最高，随机游走搜索策略的成功率最低。随机游走搜索策略减小了网络查询的流量，实现起来也比较方便。但随机游走搜索策略在选择邻居节点时缺乏偏好性。因此，随机游走搜索策略的平均搜索步数较高，搜索的成功率和搜索效率均较低。

图6 成功率与网络规模的关系

图7比较了在BA无标度的网络中最小聚类系数最小距离策略与最小聚类系数搜索策略和贪婪算法的搜索效果。图7(a)为随机选取200对节点间搜索时间的平均值与网络规模的关系，可看出无论是从搜索步数还是覆盖步数而言，最小聚类系数最小距离搜索策略均是最优的，且这种优势随着网络的增大而愈加明显。

4 结束语

文中建立了一个一般性的BA无标度网络模型。在此基础上，提出了最小聚类系数最小距离搜索策略。该搜索策略在搜索过程中的每一步，源节点和收到信息的节点会将信息传递给聚类系数最小，且离目的节点较近的邻居节点。随后，将最小聚类系数最小距离搜索策略、最小聚类系数搜索策略、随机搜索策略和贪婪算法应用到BA无标度网络上。通过比较与分析可以发现，在不同情况下，最小聚类系数最小距离搜索策略的平均路径长度要比其他搜索策略短，成功率要比其他搜索策略高。因此，得出结论最小聚类系数最小距离搜索策略更适用于BA无标度网络。

图7 3种算法搜索效果比较图

［1］ 汪小帆，李翔，陈关荣．复杂网络理论及其应用［M］．北京:清华大学出版社，2006．

［2］ Adamic L A，Adar E．How to search a social network［J］．Social Networks，2005，67(1):35 －37．

［3］ Jae Dong Noh，Heiko Rieger．Random walks on complex networks［J］．Physical Review Letters，2004，92(11):70 － 77．

［4］ 王大骄，汀小帆．无标度网络的最大－最小度搜索算法［J］．计算机仿真，2007，24(9):161 －194．

［5］ Newman M E J，Watts D J．Renormalization groupanalysis of the small－ world network model［J］．Physics Letters A，1999，263(10):341 －346．

［6］ Boguna M，Krioukov D，Claffy K．Navigability of complex networks［J］．Nature Physics，2009，5(8):74 －80．

［7］ Newman M E J．The structure and function of complex networks［J］．Society for Industrial and Applied Mathematics Review，2003，45(5):167 －256．

［8］ 冯立雪．结合最大度与最小聚类系数的复杂网络搜索策略研究［D］．北京:北京交通大学，2011．

［9］ Adamic L A，Lukose R M，Puniyani A R，et al．Search in power－ lawnetworks［J］．Physical Review:E，2001，64(5):91－97．

［10］ Thadakamalla H P，Albert R，Kumara S R T．Search in weighted complexnetworks［J］．Physical Review:E，2005，72(9):111－119．

［11］ Guimera R，Mossa S，Turtschi A，et al．The worldwide air transportation network:Anomalous centrality，community structure，and cities global roles［J］．Proceedings of the National Academy of Sciences，2005，102(11):7794 －7799．

［12］ Albert R，Barabasi A L．Statistical mechanics of complex networks ［J］．Reviews of Modern Physics，2002，74(1):47－55．

［13］ Galstyan A，Musoyan V，Cohen P．Maximizing influence propagation in networks with community structure［J］．Physical Review E，2009，79(345):314 －319．

［14］ Barabasi A L，Albert R．Emergence of scaling in random networks［J］．Science，1999，286(7):509－512．