放射形专用线非直达车流取送方案研究

朱海笑，牛慧兰，雍安娜

(兰州交通大学交通运输学院，甘肃兰州 730070)

取送车作业是货物作业较多车站的一项重要技术作业。在专用线上，取送车作业过程是指调车按照车站调度制定好的送车顺序，将列车送至专用线装卸点或仓库，待装卸作业完成后再按照一定的顺序取回车辆［1］。在专用线上取送的车流按照编发形式分为直达列车与非直达列车，非直达列车取回的车辆经过编组后由就近的小运转列车按非直达方式挂走。在调车作业中，取送车作业时间是最长的，因此，合理地安排取送作业，将有利于提高调车作业效率，缩短货车在站停留时间。许多学者已经对此问题进行了深入的研究，例如文献［2］针对放射形专用线非直达车流进行了分析，提出了不利方案的判别方法和基于枚举法的中断时间筛选法。文献［3］给出了送车和取车需要时间，提出送车增量和取车增量的概念，用以替代目标函数，简化计算。文献［4］为了提高计算效率，将禁忌搜索算法同时用于送车方案和取车方案的求解过程，验证了算法的有效性。本文在以上文献的基础上，讨论放射形专用线非直达列车在“整列到达，分散出发”模式下的取送车优化。

1 问题描述

1.1 问题分析

非直达车流的特点是先取回的车辆可随就近车次挂走，不同专用线上车组的在站停留车小时不一样，先挂走的车辆在站停留时间较短。在有关参数一定的条件下，所有车辆在站停留车小时依赖于取送顺序，为此，将该问题的优化目标设为某时段内全部车辆在站停留总车小时最少。为便于讨论，假设以下条件:(1)待送车辆成列到达，列车到达时刻已知。解体后送往各专用线的车组取送优先级别一致。(2)各专用线的装卸能力满足对入线货车同时进行货物作业;调机对需要取送的车辆数不加限制。(3)各专用线的货物作业时间大于调机取送作业时间。(4)各专用线车辆取回站内后随就近小运转列车挂走，各次小运转列车出发时刻已知。(5)只有一台调机担当取送车作业。

1.2 变量描述及模型

(1)将所有专用线编号，用i表示第i条专用线，i=1，2，…，n。(2)用 mi表示在第 i条专用线作业的车数。(3)用t货i表示第i条专用线上车辆的货物作业时间。(4)用t走i表示第i条专用线上的取(送)走行时间，2t走i即为取(送)车作业往返走行时间。送车时包含的单项作业有挑选车组和对货位，取车时包含的单项作业有收集车辆和分解车组，为简化计算，假定这两项作业时间都为定值且已包含在走行时间 t走i内。(5)用 t发i表示送往第i条专用线的车组从专用线取回之后，其挂运的就近列车出发时刻。(6)用ti表示在第i条专用线作业的车组总在站停留时间。因此，本问题的目标函数可表示为

1.3 解的表示方法

由于取送作业包含送车和取车两部分内容，故一个解x必须包含一个送车顺序和一个取车顺序，例如有四条专用线的车站，(2413，4231)即为一个取送方案，其中数字代表专用线的编号，解的前半部分表示送车方案，后半部分表示取车方案。

当有n条专用线时，解的方案数就有(n!)2个，在所有方案中寻优，过程较慢，尤其当n很大时，就会产生组合爆炸，寻找最优解就会比较困难，所以尽快缩小搜索范围具有意义的。研究表明，即使送车方案是最佳的，在其基础上产生的取车方案也是最佳的，二者合起来却不一定是最佳的取送方案［3］。因此，本文在求解时，将取送过程统一起来，但通过一定的方法产生较优的初始解，以保证满意解的质量。

2 求解思路

直接用式(1)计算目标值比较困难，必须经过一定的转化，而且直接从取送方案也难以看出各车组的挂运车次，针对这两个问题，提出如下解决方法。

(1)车辆在站停留时间是从车辆整列到达时起至随小运转列车出发时止，每个ti都包含到、解、编、发作业时间 t到，t解，t编，t发在内。通常可认为上述 4 个作业时间是定值，故令

其中，t容i为i专用线车辆挂线车次的容许挂运时间

式中，t0为车辆整列到达时刻，为简化换算，将t0置为0，t发i根据t0的实际时刻转化为相距时间，例如整列到达时刻为9点30分，第一条专用线的车组取回后挂运车次的出发时刻为12点30分，则t1发=180，将目标函数进一步转化为

由于 mi和(t到+t解+t编+t发)都是定值，故目标函数中第二项可以省略，目标函数简化为

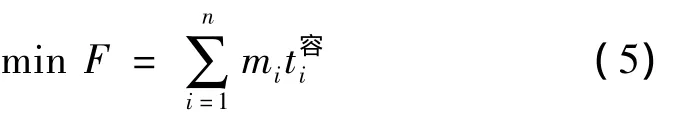
计算时，将到达和解体过程全部后移，使其与编组出发相连，又因该4项时间为定值，故在目标函数中可去掉，这样的转化简化并缩小了目标值，但并不会影响最优解。

(2)将所有小运转列车按照出发先后顺序编号，j=1，2，…，n，然后计算出 t容j。确定各线的车组挂运车次时，根据车组取回时间，找到最接近的t容j，令 j=i，即确定了i专用线车组的挂运车次。

3 求解算法

使用禁忌搜索算法的全局搜索能力，将取送顺序看做一个整体优化。局部搜索的缺点是太贪婪地对某个局部区域以及其邻域搜索，而禁忌搜索对于找到的一部分局部最优解，有意识地避开，从而获得更多的搜索区间，这对于搜索到更满意的解是有利的。它通过局部邻域搜索机制和相应的禁忌准则来避免迂回搜索，并通过藐视准则来赦免一些被禁忌的优良状态，进而保证多样化的有效探索，以最终实现全局优化。算法的主要参数如下:

(1)适值函数。适值函数用于对搜索状态进行评价，规定式(5)作为适值函数。

(2)初始解。禁忌搜索是一种基于邻域搜索的算法，对于初始解具有较强的依赖性。一个较好的初始解可导致最终在解空间中搜索到更好的解，而一个较差的初始解则会降低算法收敛速度，搜索到的解相对较差。为此，人们往往先使用某种算法获得一个满意的初始解来提高算法性能。对于送车方案，本文按送车效率 ηi=mi/t走i降序排列的方法产生初始解。对于取车方案，按照ΔP的升序方法产生

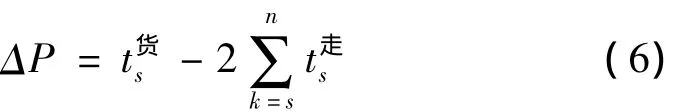
其中，ΔP表示该专用线货物作业所需时间与送车结束后立即取车为其提供的货物作业时间之差，即由于货物作业未完成而产生的中断时间，s是i专用线的送车顺序号，按其升序作为取车顺序保证了货物作业先结束先取的原则［5］。

(3)移动。移动是从当前解产生新解的途径。在本文中采用两两专用线的送(取)车顺序对换的方法，每次迭代都会从当前解产生C2n个新解。

(4)禁忌对象和禁忌长度。禁忌对象可以选取当前的值作为禁忌对象放进禁忌表，也可以把和当前值在同一“等高线”上的都放进禁忌表。

禁忌长度是被禁对象不允许选取的迭代次数，一般给定一个数t，要求被禁对象在其后的t步迭代内被禁，每迭代一次，禁忌次数减1，直到次数为0时解禁。

(5)藐视准则和终止准则。

藐视准则:若禁忌对象对应的适配值优于当前值，则无视其禁忌属性而仍采纳其为当前选择。

终止准则:当与最优解的距离连续若干步保持不变，或总迭代次数达到一个充分大的数K时，则终止搜索。本文采用总迭代次数达到一定值的方法，当n取不同值时，K可以相应的变化，文中n=6，取K=30。

4 算法步骤

Step1给定算法参数，按照上文方法产生初始解x，置禁忌表为空。

Step2判断算法终止条件是否满足。若是，则算法结束并输出优化结果;否则，继续Step3。

Step3利用当前解的邻域函数产生其所有(或若干)邻域解，并从中确定若干候选解。

Step4对候选解判断藐视准则是否满足。若成立，则用满足藐视准则的最佳状态y替代x成为新的当前解，即x=y，并用与y对应的禁忌对象替换最早进入禁忌表的禁忌对象，同时用y替换历史最佳状态，然后转Step6;否则，继续以下步骤。

Step5判断候选解对应各对象的禁忌属性，选择候选解集中非禁忌对象对应的最佳状态为新的当前解，同时用与之对应的禁忌对象替换最早进入禁忌表的禁忌对象元素。

Step6转Step 2。

5 应用实例

5.1 实例计算

已知某站某日8:00到达本站货物作业车一列，需送往各专用线作业。(t到+t解+t编+t发)共 50 min，各专用线作业车数、取送走行时间及货物作业时间如表1所示，小运转列车出发时刻如表2所示。

表1 各专用线作业车数、走行时间及货物作业时间

表2 小运转列车出发时刻

表2中的小运转列车出发时刻已按照本文的转化方法转化为最晚编组时刻与整列到达时刻的差值。经计算，得到满意解为x=(436251，342651)，F=12 350(车·min)，取车结束时间为316 min，调车中断时间为4 min，各专用线车组挂线车次如表3所示。

表3 各专用线车组挂线车次

其中，第2条专用线和第6条专用线挂同一车次出发。

图1 适应度函数变化图

5.2 结果分析

(1)本方案满意解的中断时间为4 min，虽然从表面来看调机产生了中断取送时间，作业不够紧凑，但从整体目标值来看却比有些中断时间为0的方案更优。例如方案(435261，534261)调机送完车可立即取车，无中断时间，但该方案目标值为12 920车·min，远劣于12 350车·min。

(2)随着专用线数的增加，取送方案数急剧增加，此时较好的初始解对随后的搜索收敛非常重要。例如文献［2］中，当n=8时，全部方案数达到了1 625 702 400，利用中断时间筛选法淘汰第一类不利方案后，仍有191 415 588个方案，求解用时达36 min［2］。利用本文方法产生一个较优的初始解(23587614，25731864)，该方案的目标值为348.6车·h，已非常接近文献中的最优解346.1车·h。而在迭代过程中，本文方法在每次迭代最多只需在C28=28个候选解中搜索，大幅减小了搜索难度和时间。因此，当n较大时，利用本文算法求满意解是有利的。

6 结束语

放射形专用线非直达车流取送车方案随着专用线数的增加而急剧增大，尽快搜索到满意解非常重要。鉴于禁忌搜索算法对初始解的依赖性，本文对送车和取车初始解分别利用一定的优化方法，产生较好的初始解，以保证算法最终解的满意度。本文将取送过程整体化，避免了无调机中断时间的局部最优方案。

［1］彭光明.企业铁路运输放射状取送车作业优化方法研究［D］.长沙:中南大学，2012.

［2］谢金宝.非直达车流取送方案的中断时间筛选法研究［J］.兰州交通大学学报，2009，28(3):95 －99.

［3］王慈光.放射形专用线非直达车流取送车问题研究［J］.交通运输工程与信息学报，2006，4(3):16－23.

［4］谢金宝.非直达车流取送方案的禁忌搜索算法研究［J］.交通运输系统工程与信息，2010，10(1):158－163.

［5］胡思继.铁路行车组织［M］.北京:中国铁道出 版社，2009.

［6］宋建业.直达列车多点装卸取送顺序优化的表上移动法［J］.兰州铁道学院学报:自然科学版，2002(1):76－79.

［7］刘林忠.最优化理论与算法［M］.兰州:兰州交通大学出版社，2007.

［8］刘兴，贺国光.车辆路径问题的禁忌搜索算法研究［J］.计算机工程与应用，2007，43(24):179 －180.

［9］牟峰，王慈光，杨运贵.放射形专用线非直达车流取送车模型及算法［J］.铁道学报，2009，31(3):1－5.