管道弯曲塑性屈曲应变的评价
郑茂盛,胡 军,滕海鹏,赵 渊
(西北大学化工学院 载能技术及应用研究所,西安710069)
管道弯曲塑性屈曲应变的评价
郑茂盛,胡 军,滕海鹏,赵 渊
(西北大学化工学院 载能技术及应用研究所,西安710069)
概述了目前的几种管道弯曲屈曲临界应变预测评估方法,重点介绍了弯管横截面椭圆化的理论解决方案,并分析了它们各自的适用性。为了确定目前最合理有效的预测评估方法,对几种管道弯曲屈曲临界应变公式的预测结果与试验数据以及有限元计算结果进行了对比分析。分析结果表明,针对管道弯曲屈曲临界应变的预测,在大多数情况下,屈曲塑性变形引起的截面椭圆模型给出的预测结果比其他屈曲应变预测方法的结果更切实际。
弯管;屈曲临界状态;横截面椭圆化;塑性变形;评价
对石油和天然气输送而言,管道运输被公认为是最为经济合理的运输方式。目前,全球天然气和石油管道的总长度超过2.3×106km,并且以每年(2~3)×104km的速度增长。由于管道的实际使用环境条件是复杂多变的,埋地管道在一些地区甚至可能会遭受地质灾害和地震影响,从而会使管道在服役期间不可避免地产生较大的位移,甚至应变。因此,应力不再是管道失效的唯一控制因素,而应变或位移将部分或全部地成为决定性因素[1-2]。
屈曲几乎总是伴随着弯曲失稳载荷发生的,一般可以用屈曲起始来定义管道的失效。弯曲荷载作用于管道时,管道横截面的形状会从圆形逐渐变为一个椭圆形。当管道横截面形状的弯曲变化超过一定值时,随着弯曲的进行弯曲荷载可能不再增加,甚至突然减少,被称为管道的屈曲失效。
早期开展管道弯矩和状态的极限点研究的是Brazier,其1927年 的研究结果[3]表明,当初始直管均匀弯曲时,管道的纵向会产生拉伸和压缩以抵抗弯矩。同时,弯曲会使管道截面扁平化或椭圆化,管道的弯曲曲率逐渐增大,从而会降低构件的抗弯刚度。Brazier也表明,抗弯刚度有一个最大值,它可以被定义为失稳点。Brazier的弹性失稳公式为
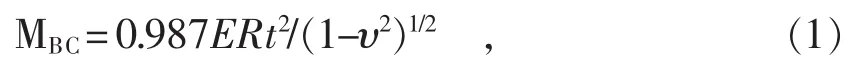
式中:R—管道横截面半径;
t—管道厚度;
E—杨氏模量;
υ—泊松比。
在Brazier开创性工作之后,研究者便开始逐渐关注这一问题。例如,Seide和Weingarten[4],Fabian[5]和Long-Yuan Li[6]等的弹性失稳分析,Jirsa[7],Sherman[8], Reddy[9], Gellin[10], Bushnell[11],Calladine[12]和 Kyriakides[13]则从试验或解析方面开展了弹塑性状态分析。
近20年来,随着纳米管行为和管道安全运行的需求,激发了人们对管件屈曲的特别兴趣,于是涌现了大量针对圆管弯曲稳定性分析的相关研究工作。M.Khurram Wadee等[14]于2006年提出的变分模型分析了薄壁弹性管在纯弯曲情况下圆形截面屈曲变形的局部化,并且以此模型分析了包括碳纳米管等的一些情况。2009年,Philippe Le Grognec和 Anh Le van[15]分析了板和圆管受均匀压力情况下的弹塑性屈曲和初始后屈曲特征,此分析涉及到三维塑性分叉理论、J2流动塑性理论和Von Mises屈服准则,以及线性各向同性硬化。该方法是一个确定单轴或双轴受压矩形板屈曲的初始分叉和圆筒轴压临界载荷的一种模式。同年,Poonaya,C.Teeboonma和Thinvongpituk等[16]分析了薄壁圆管弯曲的塑性破坏,在塑性变形区内引入了沿管纵向长度的三维斜铰线型破坏机理。在变形能量率的推导过程中,分别计算出每个铰链线的内能量耗散率和拉伸变形,并采用了理想塑性材料模型。2011年,Gianluca Ranzi和Angelo Luongo[17]提出了将广义梁理论(GBT)用于截面分析,该方法基于Kantorovich的半变分法,目的在于描述薄壁件的线弹性行为。
直到2012年,T.Christo Michael等[18]研究了管道受面内弯曲封闭力矩作用时椭圆度和变壁厚对破坏荷载的影响。有限元极限均值分析和弹—塑性材料被用于这一研究。结果表明,椭圆度显著影响了破坏荷载。最近,Gayan Rathnaweera等[19]用试验和有限元分析了铝/terocore混合结构的准静力三点弯曲。该混合结构的性能与Terocore泡沫的体积百分比和管壁厚度有关。试验观察到两种破坏模式,即从AA7075 T6的顶面失败(压缩)和高泡沫体积百分比时底面破坏结构(拉伸)。
实际上,由于埋地管道可能遭受复杂的多变环境条件,造成可能的变形或应变,导致先前所提出的强度设计准则失效,弯曲管道屈曲的临界应变值可望作为管道的设计指标[20-23]。然而,临界屈曲应变的估算仍然是一个没有完全解决的问题。直到现在,有些预测公式不是缺少物理意义,就是不合理。虽然经典的解析解的物理意义明确,其预测却与试验结果相差很远,原因在于经典的解析解属于弹性解范畴,其他的回归或拟合公式则缺乏明确的物理含义。这种情况表明,弯曲管道屈曲的临界应变估算仍然是一个重要的问题[21-22]。
1 现行的管道弯曲应变评估方法
1.1 弹性解
圆柱壳的Donnell方程为

式中:R,t,w—圆形外壳半径、厚度、挠度;
E—圆壳的弹性模量;
D—圆管的弯曲刚度, D=Et3/[12(1-υ2)];
p—沿轴向圆管的均匀应力。
方程(2)的经典(弹性)解是

对于钢,其泊松比υ=0.3,式(3)变为

相应的应变为

对于弯曲圆形的外壳,它给出了与(5)式相同的结果。
图1显示了经典理论结果与试验结果的比较。从图1可以看出,理论预测的结果比大多数试验数据都高。图1的试验数据引自文献[21]的表1和表2无压力条件下的弯曲内部变形。

图1 试验结果与经典弹性理论预测结果比较
实际上,对于一个实际的管道,径厚比一般情况下约为30~50。例如我国西气东输管线用管φ1 024 mm×20 mm, 由公式(5)可以预测出其 εcr=1.21%,大大超过了管线钢的弹性极限应变(一般在0.2%左右)。显然,尽管公式 (5)是一种具有弹性理论的预测,但其对实际管道的预测值却远远超过了弹性极限应变。这表明公式(5)的预测超过其有效范围,不适合应用到实际管道中去。
1.2 其他解
到目前为止,有关研究已经提出了一些其他的表达式,来预测弯曲管道的屈曲临界应变,具体见表1。

表1 弯曲管道的屈曲应变预测公式[21-23]
在表1中,Sherman公式是基于细长压杆的解。文献[24]给出了内部无压力状态下塑性弯曲管的D/t在18~102范围内的测试结果。图2所示为这些测试结果与Sherman公式预测结果的比较。从图2可以看出,预测结果比试验结果低得多。

图2 文献[24]中管道无压力时的测试结果与Sherman公式预测结果比较
此外,Sherman公式的预测结果与文献[21]的试验数据比较如图3所示。从图3可看出,Sherman公式所给出的预测值比大多数试验结果都低。
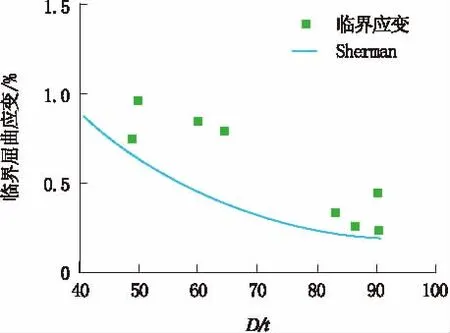
图3 文献[21]中管道无压力时的测试结果与Sherman公式预测结果比较
Stephens公式 εc=2.42(t/D)1.59是通过回归分析弹塑性弯曲管道的试验数据在有内部压力的情况下得到的解[25],它缺乏清晰的物理意义和理论基础。图4显示Stephens公式的预测结果与无内部压力环境下的测试结果的比较[21]。从图4可以看出,Stephens公式的预测值低于文献[21]的试验结果。

图4 文献[21]中管道无压力时的测试结果与Stephens公式预测结果比较
1999年,Vitali提出了回归公式[23]。Vitali等人不仅分析有限元计算结果,还分析了D/t小于60的试验测试结果,提出了临界屈曲应变方程。他们所分析的管线钢屈服强度和抗拉强度分别为450MPa和530MPa。他们考虑了D/t、内部压力、材料属性以及其他因素的影响。表2显示Vitali公式和文献[21]在内部压力状态下试验数据的对比。从表2可以看出,测试值与预测值比值的平均值为0.58,这表明预测结果几乎超越测试值100%。
1.3 有关标准
1.3.1 CSAZ662-07
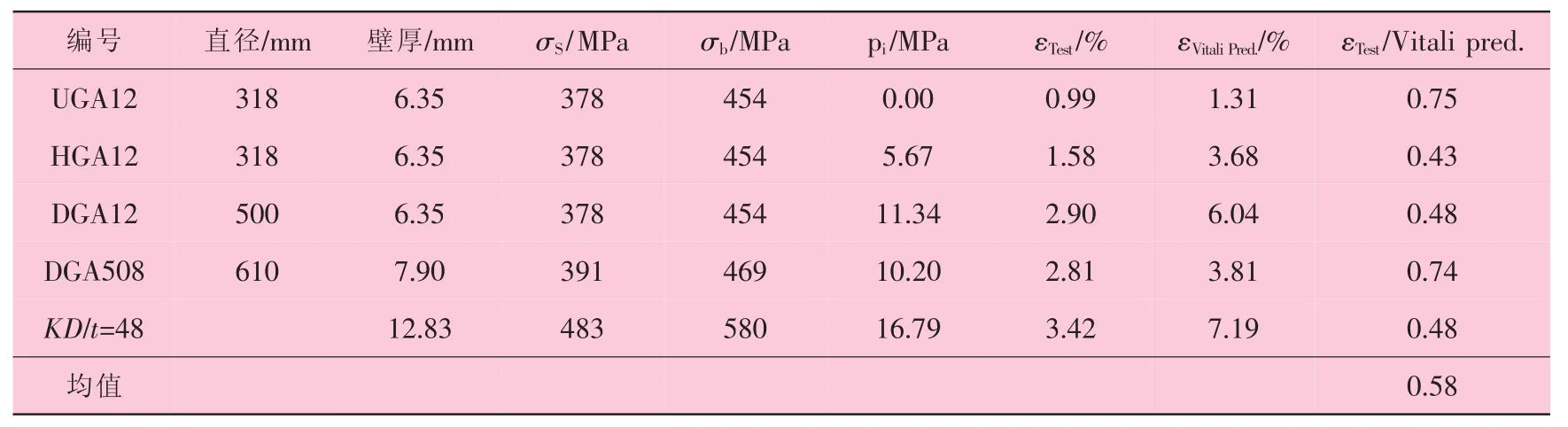
表2 Vitali公式和参考试验数据对比
CSAZ662-07-C.C6.3.3.3指出,为了防止局部屈曲,对纵向压缩一级载荷、二级载荷,或者二者同时存在时,可依照公式(6)[26]估算其临界应变

式中:εc—管壁的最大压应变能力;
t—钢管厚度,mm;
D—钢管外径,mm;
pi—最大的内部设计压力,MPa;
pe—外部的静水压力,MPa;
E—弹性模量,Es=207 GPa;
Fy—规定的最小有效屈服强度,MPa。
1.3.2 DNV-OS-F101
2000年发布的DNV-OS-F101中第507条提出了抗压弯曲应变能力εM,c的估算公式[27],
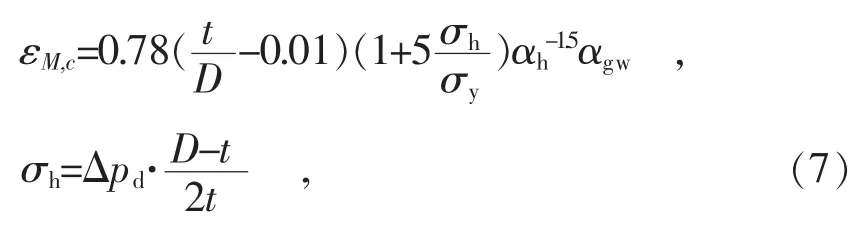
式中:t—钢管厚度;
D—钢管直径;
σh—特征环向应力;
σy—材料的屈服强度;
αh—最大屈强比;
αgw—环缝焊接系数(试样为无焊缝,取为1)。
图5给出了上述两个标准的预测值与文献[25]的试验结果的比较,图5反映出这两个标准所预测的结果,精度也较低。

图5 标准的预测值与文献[25]试验结果的比较
2 弯管横截面椭圆化的理论解决方案
2.1 Brazier的解
早在1927年,Brazier针对弯管横截面的椭圆化[3],给出了最大力矩、最大曲率和不稳定点的最大径向变形,分别为

相应地,在弯管最外侧的表观临界应变为

公式(11)中,虽然数据0.384小于经典弹性解析解0.605的结果,但它仍然比试验值[21-25]高得多。总之,它是考虑了圆管弯曲加工的横截面椭圆化的弹性解。
2.2 Long-Yuan Li的解
Long-Yuan Li等[6]采用了Brazier所提出的薄壁圆管在静态弯曲时横截面椭圆化的思想,即圆管截面的纵向压缩和拉伸应力使横截面椭圆化,如图6(a)所示。根据Brazier的假设,管道截面的典型椭圆形状[6]可以表示为

式中:u—薄壳的径向位移;
R—未变形原始壳的平均半径,是平面内半径的角坐标,如图6所示,是表征径向位移的无量纲因子。

图6 对管弯曲椭圆截面模型
Long-Yuan Li建议的横截面的变形发生在其自身的平面中,弯曲管单位长度的总势能[6]可以表示为

式中:E—材料的弹性模量;
υ—泊松比;
t—管壁的厚度;
C—弯曲管的纵向曲率,
M—瞬时弯矩。
公式(13)右边的第 1项表示纵弯曲的势能,而第2项则表示横截面的势能,第3项表示外部负载的势能。Long-Yuan Li指出如果略去(13)式中ξ2项,将可以得到Brazier的结果。
根据最小势能原理,可以得到[6]

同时,失稳的临界状态[6]为

进一步,可以得到失稳点的临界状态参数[6]

相应地,在弯管最外侧的表观临界(屈曲)应变为

显然,公式(19)中的系数 0.485比 Brazier的弹性解的系数更大。总之,它们都是在考虑了弯管截面椭圆化情况下屈曲问题的弹性解。
2.3 Tomasz Wierzbicki的塑性平截面模型
为了考虑弯管的塑性变形行为,Tomasz Wierzbicki等提出了平截面模型,以近似弯曲薄壁管截面的形状[28],如图7所示。
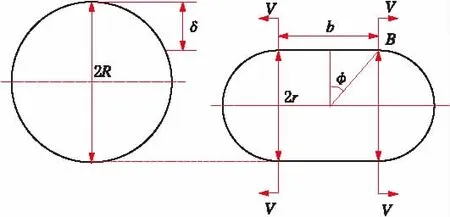
图7 Tomasz Wierzbicki的平截面弯管模型
从图7容易得到以下几何关系[28]
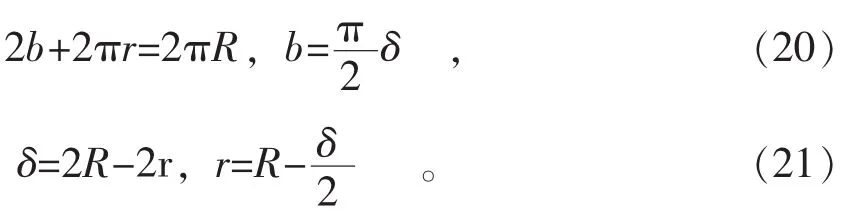
此外,根据总能量最小化和弯曲的失稳条件,Tomasz Wierzbicki给出了以下关系式
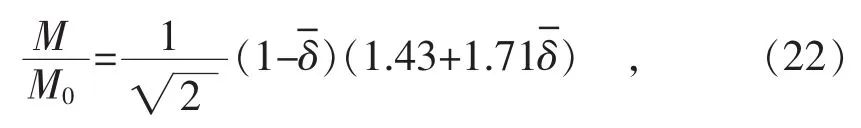
式中:M—外加力矩;
M0—刚塑性材料圆管的极限弯矩,M0=4σ0R2t;
σ0—管道材料的流动应力;
R—圆管的平均半径;
t—圆管壁厚;
从公式(22)可以得到弯曲管失稳时的无量纲变形参数的临界值

此外,他们还给了一个近似关系[28]

将方程式(23)和(24)相结合,可以得到弯曲管失稳时纵向曲率的临界值

因此,屈曲状态下弯曲管外侧的宏观应变为

综上所述,公式(26)中的系数0.141不仅远低于经典弹性解0.605,而且也低于试验值[21-25],表明Tomasz Wierzbicki的方法过分地简化了弯曲管的横截面[28]。而Brazier模型给出的εC=0.384 t/R,虽然其数值0.384小于经典弹性理论的结果0.605,但仍远高于试验值[21-25],并且是一种弹性解[3]。
2.4 弯管截面塑性的椭圆化模型
在文献[1]中,假设管道在弯曲过程中其截面脱离圆而逐渐变成为椭圆。此外,管材也是刚性—完全塑性的。并且针对钢管截面的椭圆化,应用能量法建立了宏观弯矩Me随弯曲变形参量γ之间的变化关系,以及失稳时的宏观最大弯矩管和临界屈曲应变的表达式

式中:Me—宏观弯矩。


相应地,临界状态下弯管外侧的宏观屈曲应变为
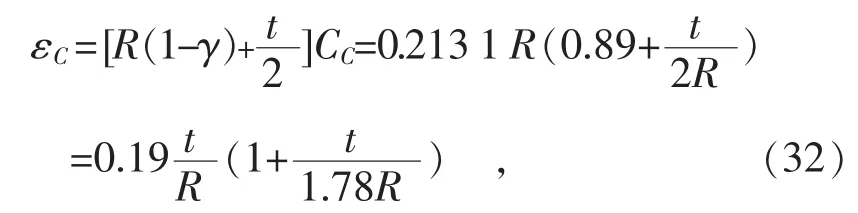
公式(32)中的系数值0.19接近于试验结果[21-25]。
在文献[1]中,采用了文献[21]测试数据检查了其有效性,获得了良好的结果。
2.5 弯管截面椭圆化塑性模型的再检验
为了做进一步的检验,将取自其他文献的弯管屈曲试验数据和有限元计算数据再次用来评估其有效性。
E.Corona等[29]曾经进行了Al-6061-T6管道的弯曲屈曲试验。管道的直径和厚度分别为D=31.75 mm和t=0.879 mm,管的长度是20D。采用四点弯曲试验进行屈曲试验。在测试期间,通过相关监测仪器检测管道的形状变化、皱纹、弯矩和其他参数的变化,结果如图8所示。
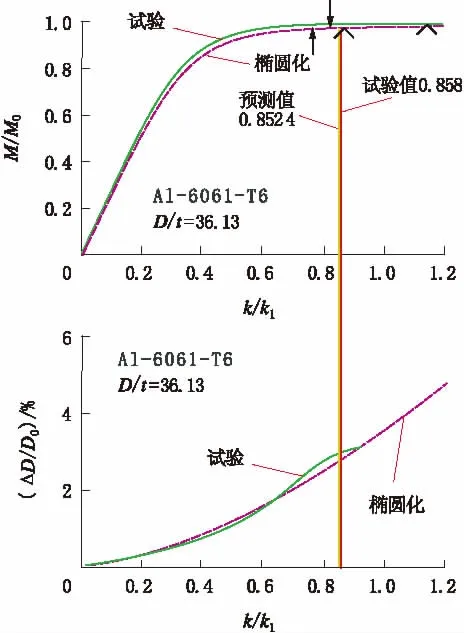
图8 E.Corona的屈曲试验与模型预测结果比较
在图8中,横坐标是规一化的曲率,其归一化参数是按照以下方式进行的,

式中:σ0—材料的屈服强度。
在图8中,以“↑”表示了管体在压缩侧观察到第一个皱折点,它出现在k=0.751 k1处,此后沿管子长度方向上的椭圆化不再均匀。随着弯曲过程的进行,会达到最大弯矩,在图8中以符号“^”显示的最大弯矩点,这是管道屈曲的灾难性失效点。同时,图8还给出了按照公式(31)所预测的失效点位置。
从图8可以看出,管道到达临界点的曲率最大弯矩系数k=0.858 k1,而塑性椭圆截面模型公式(31)的预测值为k=0.8524 k1,两者的相对误差是0.653%。
Kyriakides S和Ju G T以Al-6061-T6铝管为研究对象,作了D/t从19.5到60.5之间的一系列的试验[30]。图9和图10分别给出了D/t=32.2和D/t=19.5时的试验结果,其中还显示了公式(31)的预测情况。

图9 Kyriakides测试结果与模型预测结果对比(D/t=32.2)
从图9可以看出,D/t=32.2的Al-6061-T6管道达到最大弯矩点时的临界曲率kb=0.94 k1,公式(31)的预测值kc=0.852 4 k1,二者相对误差为9.3%。
从图10可以看出,D/t=19.5的Al-6061-T6管道达到最大弯矩点时的临界曲率kb=0.95 k1,公式(31)的预测值kc=0.852 4 k1,二者相对误差为10.27%。
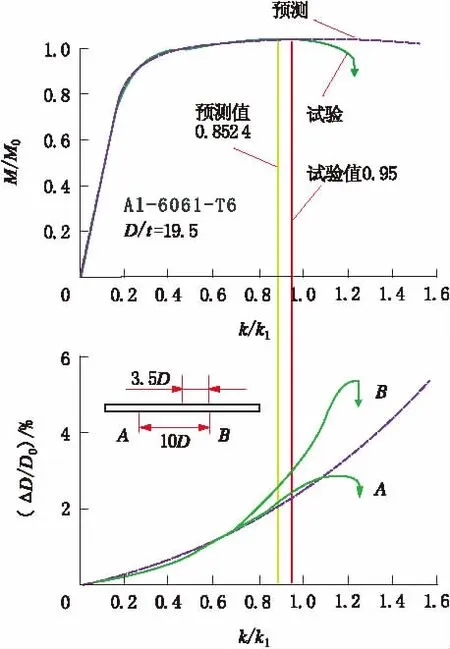
图10 Kyriakides测试结果与模型预测结果比较(D/t=19.5)

表3 Kyriakides S等人试验值和公式(31)预测值对比
表3列出了Kyriakides S等人一系列的试验值[30]和公式(31)预测值结果,并给出了相对误差。
从表3可以看出,文献[1]所提出的预测公式与Kyriakides的测试结果基本一致。
Minnaar K等人在基于弹塑性有限元模拟的基础上,得到了对应的临界应变值[31]。对应的分析方法和结果目前已被挪威船级社标准 DNVOS-F101《海底管线系统》采纳。Minnaar的公式为

式中:αh—屈服强度与极限抗拉强度的比值。
此处将Minnaar K基于弹塑性有限元分析数据和基于弯管截面椭圆化的塑性模型的临界应变预测公式分别就X70,X80和X100管线钢进行了比较。
对于X70管线钢,从文献[32]得到的抗拉强度为 668 MPa,屈强比为 0.810,弹性模量为207 GPa。得到的预测结果如图11所示。

图11 X70管线钢的临界屈曲应变预测结果
从图11可以看出,对于X70管线钢而言,基于弯管截面椭圆化的塑性模型的临界应变的计算公式和Minnaar K等人基于有限元方法得到的结果非常接近,表明基于弯管截面椭圆化的塑性模型的预测公式(33)对X70管线钢的预测结果是合理的。
对于X80管线钢,从文献[32]得到的抗拉强度为751 MPa,屈强比为0.847,弹性模量为207GPa。得到的预测结果如图12所示。
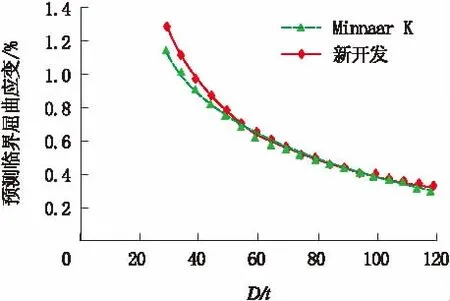
图12 X80管线钢的临界屈曲应变预测结果
从图12可以看出,对于X80管线钢而言,基于弯管截面椭圆化的塑性模型的临界应变的计算公式和Minnaar K等人基于有限元方法得到的结果的误差也较小,所以基于弯管截面椭圆化的塑性模型对X80管道进行安全评估时也是可行的。
对于X100管线钢,从文献[32]得到的抗拉强度为812 MPa,屈强比为0.87,弹性模量为207GPa。得到的预测结果如图13所示。
从图13可以看出,对于X100管线钢而言,基于弯管截面椭圆化的塑性模型的临界应变的计算公式(32)和Minnaar K等人基于有限元方法得到的结果相比差别也很小。所以,基于弯管截面椭圆化的塑性模型对X100管道进行安全评估时也是可行的。

图13 X100管线钢的临界屈曲应变预测结果
Guarracino F等人也对一些评估方法和测试数据[33-34]进行了比较。图14给出了这些方法与在文献中的测试结果的比较[33-34]。此外,还显示了公式(32)的预测曲线。Guarracino F等人所涉及的极限应变公式[33-34]为

式中:D0—外管道直径;
t—外管道厚度。

图14 不同D/t时文献中试验结果与预测结果的对比
图14给出了不同D/t对应的临界屈曲应变[34-35]。从图14可以看出,Gresnigt表达式、Murphey表达式和公式(32)均可得到比较好的预测结果,并且均在相对安全的区域。但是,公式(32)是在弯曲管截面椭圆化的塑性模型和刚性—理想塑性材料模型的条件下推导出来的,具有明确的物理含义。
3 结 语
通过上述分析和讨论可以看出,弯曲管横截面的塑性椭圆化模型所给出的临界屈曲应变预测公式是最有效和合理的方法。该模型在推导时的基本假设是,弯曲管的横截面椭圆化和刚性-理想塑性材料模型。它不仅体现了管道弯曲变形时的真实现象,而且抓住了管材在弯曲变形时的主要特征,因此给出了更为合理的预测结果。
[1]JI L K,ZHENG M.Apparent strain of a pipe at plastic bending buckling state[J].Brazilian Soc.of Mech.Sci.&Eng.,DOI 10.1007/s40430-014-0302-4.Jan.
[2]ROBERTSON A,LI Hongjun,MACKENZIE D.Plastic collapse of pipe bends under combined internal pressure and in-plane bending[J].International Journal of Pressure Vessels and Piping,2005(82):407-416.
[3]BRAZIER L G.On the flexure of thin cylindrical shells and other thin sections[J].Proc.Roy.Sot.Series A,1927(116):104-114.
[4]SEIDE P,WEINGARTEN V I.On the buckling of circular cylindrical shells under pure bending[J].J.Appl.Mech.,ASME,1961(28):112-116.
[5]FABIAN O.Collapse of cylindrical elastic tubes under combined bending,pressure and axial loads[J].Int.J.Solids Structures,1977(13):1257-1270.
[6]LILongyuan.Approximateestimatesofdynamicinstability of long circular cylindrical shells under pure bending[J].Int.J.Pres.Ves.&Piping,1996(61):37-40.
[7]JIRSA J O,LEE F K,WILHOIT J C,MERWIN J E.Ovaling of pipeline under pure bending[J].OTC 1569,Proc.Offshore Tech.Conf.,1970(I):573-582.
[8]SHERMAN D R.Tests of circular steel tubes in bending[J].J.Struct.Div.ASCE,1976(102):2181-2195.
[9]REDDY B D.An experimental study of the plastic buckling of circular cylinders in pure bending[J].Int.J.Solids Structures,1979(15):669-683.
[10]GELLIN S.The plastic buckling of long cylindrical shells under pure bending[J].Int.J.Solids Structures,1980(16):397-407.
[11]BUSHNELL D.Elastic-plastic bending and buckling of pipes and elbows[J].Comp.Struct.,1981(13):241-254.
[12]CALLADINE C R.Plastic buckling of tubes in pure bending,in Collapse,the Buckling of Structures in Theory and Practice(edited by J.M.T.Thompson and G.W.Hunt)[J].Cambridge University Press,1983:111-124.
[13]KYRIAKIDES S,SHAW P K.Inelastic bending of tubes under cyclic loading[J].J.Pressure Vessel Tech.,ASME,1987(109):169-178.
[14]KHURRAM WADEE M,AHMER WADEE M,ANDREW P B,ANDREAS A A.Longitudinally inhomogeneous deformation patterns in isotropic tubes under pure bending[J].Proc.R.Soc.A,2006(462):817-838.
[15]PHILIPPE Le Grognec,ANH Le van.Some new analytical results for plastic buckling and initial post-buckling of plates and cylinders under uniform compression[J].Thin-Walled Structures,2009(47):879-889.
[16]POONAYA S,TEEBOONMA U,THINVONGPITUK C.Plastic collapse analysis of thin-walled circular tubes subjected to bending[J].Thin-Walled Structures,2009(47):637-645.
[17]GIANLUCA Ranzi,ANGELO Luongo.A new approach for thin-walled member analysis in the frame work of GBT[J].Thin-Walled Structures,2011(49):1404-1414.
[18]CHRISTO M T,VEERAPPAN A R,SHANMUGAM S.Effect of ovality and variable wall thickness on collapse loads in pipe bends subjected to in-plane bending closing moment[J].Engineering Fracture Mechanics,2012(79):138-148.
[19]GAYAN Rathnaweera,DONG Ruan,MICHAEL Hajj,YVONNE Durandet.Performance of aluminum/Terocorehybrid structures in quasi-static three-point bending:Experimental and finite element analysis study[J].Materials and Design,2014(54):880-892.
[20]LI H L.Development and application of strain based design and anti-large-strain pipeline steel[J].Petroleum Sci.&Tech.Forum(in Chinese),2008,27(02):19-25.
[21]DOREY A B,MURRAY D W,CHENG J J.An experimental evaluation of critical buckling strain criteria[C]//2000 International Pipeline Conference,Vol.1,Calgary,Alberta,Canada:[s.n.],2000:71-80.
[22]DOREY A B,MURRAY DW,CHENG J J.Critical buckling strain equations for energy pipelines—A Parametric Study[J].Transaction of the ASME,2006(128):248-255.
[23]VITALI L,BRUSCHI R,MORK K J,et al.Hotpipe project-capacity of pipes subjected to internal pressure,axial force and bending moment[C]//Proceedings of the 9th international offshore and polar engineering conference.Brest:The international society off offshore and polar engineering,1999:22-33.
[24]SHERMAN D.Tests of circular steel tubes in bending[J].ASCE journal of structural division,1976 (102):2181-2195.
[25]STEPHENS D R,OLSON R J,ROSENFELD M J.Topical report on pipeline monitoring-limit state criteria[R].Columbus:Battelle,NG-18 Report No.188.
[26]Z662—2007,Oil and gas pipeline systems and special publication,Z662.1-07,Commentary on CSA[S].
[27]DNV,Offshore Standard,DNV-OS-F101:2000, Subma-rine pipeline systems[S].
[28]WIERZBICKI T,MONIQUE V S.A simplified model of Brazier effect in plastic bending of cylindrical tubes[J].Int.J.Pres.Ves.&Piping,1997(71):19-28.
[29]CORONA E,LEE L H,KYRIAKIDES S.Yield anisotropy effects on buckling of circular tubes under bending[J].Int.J.of Solids Structures,2006(43):7099-7118.
[30]KYRIAKIDES S,JU G T.Bifurcation and location instability in cylindrical shells under bending-I experiments[J].Int.J.of Solids Structures,1992,29(09):1117-1142.
[31]MINNAAR K, DUFFY B W, OLSO E, et al.Structural designcapacity of X120linepipe[C]//Proceeding so finternational pipeline conference.Calgary,Canada: [s.n.],2004:1751-1760.
[32]ZHANG X,FENG Y,ZHAO W,et al.Microstructure and mechanical properties of X80 pipeline steel[J].Special Steel, 2006,27(3):11-17.
[33]GUARRACINO F,FRALDI M,GIORDANO A.Analysis of testing methods of pipelines for limit state design[J].Applied Ocean Research, 2008(30):297-304.
[34]GRESNIGT A M,VAN FOEKEN R J.Local buckling of UOE and seamless steel pipes[C]//ISOPE conference 2001.[s.l.]:ISOPE Conference,2001:131-142.
Assessment on Pipeline Plastic Bending Buckling Strain
ZHENG Maosheng,HU Jun,TENG Haipeng,ZHAO Yuan
(Institute for Energy Transmission Technology and Application,School of Chemical Engineering,Northwest University,Xi’an 710069,China)
In this article,it introduced current several assessment methods for assessing pipeline plastic bending buckling strain,emphasized the theory solution of bending pipe cross-section ovalization,and analyzed the applicability.In order to determine the most reasonable and effective prediction assessment method,the comparison among prediction of pipe bending critical buckling strain formula,test data and finite element calculation results was conducted.The analysis results indicated that the section elliptical model prediction result caused by buckling deformation is more reasonable than that of other buckling strain prediction in most cases.
bending pipe;buckling critical state;cross-section ovalisation;plastic deformation;assessment
TE832
A
1001-3938(2015)10-0019-09
郑茂盛(1962—),西北大学教授、博士生导师,长期从事能源材料和技术的研究与开发工作。
2015-07-07
罗 刚

