地震管道的横向平稳随机振动

冉龙飞，王天群

（辽宁石油化工大学，辽宁 抚顺113001）

地震管道的横向平稳随机振动

冉龙飞，王天群

（辽宁石油化工大学，辽宁 抚顺113001）

针对地震作用对埋地管道的影响程度，应用数值计算方法得到振型函数的解析解。该计算方法假设埋地管道的平稳随机振动是线性振动的问题，即管—土系统的激励和响应都具有零均值，以此得到的协方差函数和相关函数是等同的。根据求解埋地管道平稳振动解析解的方法，分析管道的横向振动情况。结果表明，对于横向振动，管道中部应力和位移趋于恒定，边界区域的应力和位移是变化的，埋地管道的横向平稳振动的最大应力发生在滑动边界上。

地震；管道；数值计算；振动；解析解

地震的发生是一种突发状况，很难预测。实际上，地震灾害发生时，地下某处薄弱土层突然在外界载荷的作用下发生震动，并且以波的形式辐射至周围土层，引起地面剧烈晃动，埋地管道由于受到地面振动的影响一起发生振动，这种随机振动对管道破坏力极强[1-2]。

地震波是由断层的不规则滑动而引发的，这种振动形式很快引起地面结构发生变化，在此过程中，地震波的强弱是变化的，造成管道和地面的振动也是随机的，因此，对地面采用随机过程模型是符合实际情况的。管道的随机振动分析包括平稳随机振动、非平稳随机振动及参数随机变化的振动分析。为了简化计算过程，笔者仅分析地面管道振动的平稳过程[3-4]。

1 管道横向振动的基本方程及其特征解

一般情况下，埋地管道的运动可以分解成两个方向的运动，一是沿轴向振动，二是垂直管道轴向引起管道横向振动即弯曲振动。横向振动的模型如图1所示，图1是两端滑动的边界条件。土壤对管道的作用包括土弹簧作用和阻尼作用[5-6]。

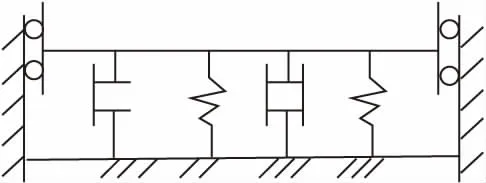
图1 管道横向振动模型

横向振动的基本方程[7]为

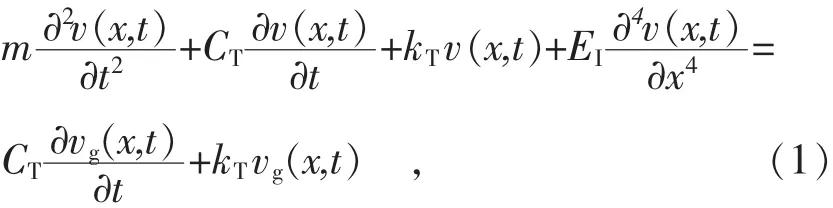
式中： v（x,t）—绝对横向位移；

vg（x,t）—地震地面位移；

m—管子单位长度质量；

CT—土壤的阻尼系数；

kT—土壤的弹簧系数；

EI—管子的弯曲刚度。

令方程（1）中

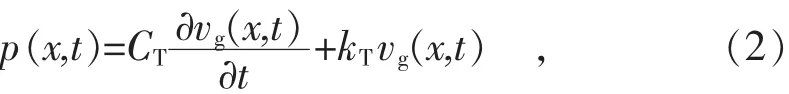
令方程（2）中

得到埋地管道自由振动方程

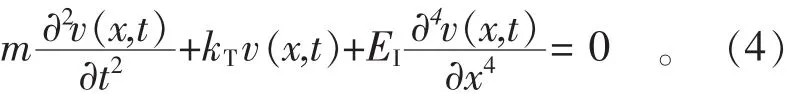
应用数学物理方程中介绍的分离变量法求解方程 （4）的特征值，得到如图1所示两端滑动边界条件下埋地管道的固有频率和模态函数[8-9]为

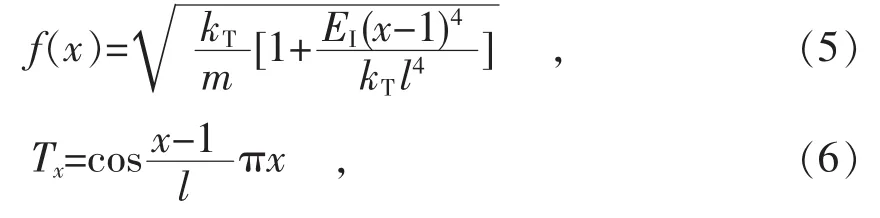
式中：Tx—模态函数；

x—位移；

l—管长。

2 地震地面的平稳随机运动

埋地管道在地震作用下管道的运动是随机的，尽管随机运动过程很难达到平稳条件的要求，但是当一个随机运动过程在参数区间无限长的情况下是均匀的，也可近似看作是平稳过程。平稳过程要求函数在整个取值区间都有定义，且统计特性对远点的选取有一定的均匀性[10]。

地震时地面运动加速度是随机变化的，开始逐渐变大到中间平稳阶段及最后逐渐减小。地震发生时，地面发生持续平稳震动，且埋地管道的强震反应也发生在这段时间内，所以可将地震地面加速度过程简化为平稳随机过程[11]。

地震载荷常用功率谱密度函数[10]表达，即

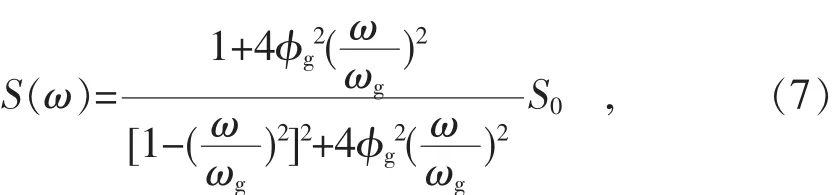
式中：ω—地震波动频率；

ωg—地基固有频率；

φg—地基阻尼比。

运用公式（7）分析地震管道的运动情况，需对其进行进一步修正才可以使用。

3 平稳横向振动

地震时，地面运动加速度的互功率谱密度[13-14]可以表示为

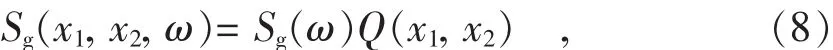
横向振动的互功率谱可以表示为

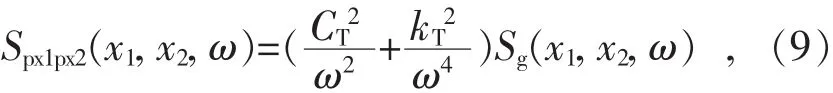
引入变换

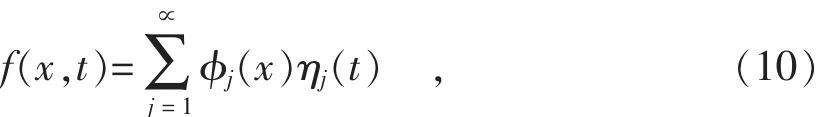
得到求解位移响应的互相关函数和互功率谱密度的相互无关微分方程组[15]

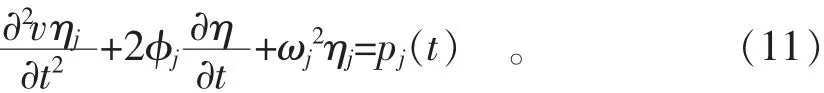
求解上述方程，得到埋地管道两端滑动模型，横向振动管道弯曲应力的功率谱密度为

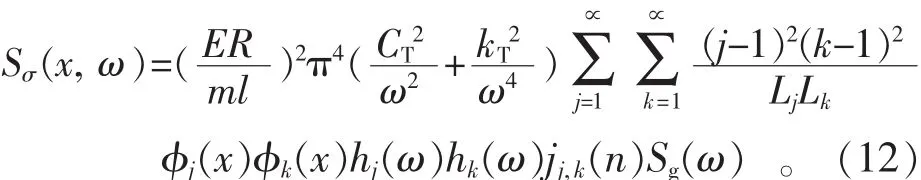
4 分析与讨论

选取某条管径为508 mm，壁厚为8.7 mm的管道，kA=kT=7.55×106N/m2，地震裂度为 7级。根据上述条件对埋地管道横向振动情况下的应力和位移变化情况进行数值分析讨论。

选取软土和硬土中的谱密度函数，考虑埋地管道中应力和位移沿管长的变化规律，得到管道横向随机振动的应力和位移，如图2～图5所示。

分析图2～图5可知，管道中部位移和应力趋于恒定，应力和位移变化主要发生在边界处，横向振动的最大应力发生在滑动边界上。

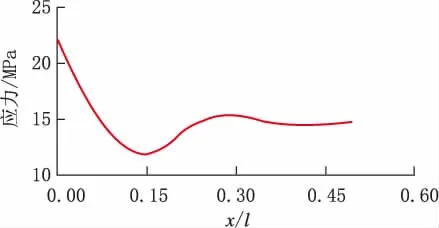
图2 软土中管道应力变化

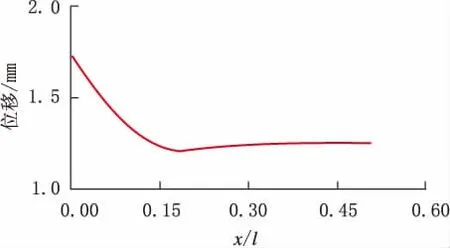
图3 软土中管道位移变化

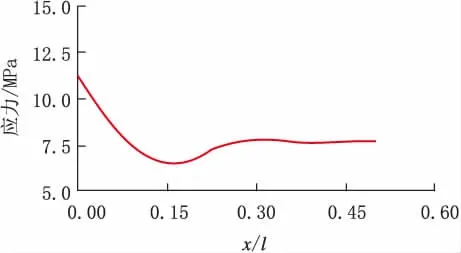
图4 硬土中管道应力变化

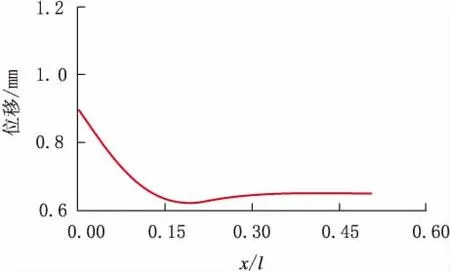
图5 硬土中管道位移变化

5 结 语

对于埋地管道遭受地震作用时地面和管道横向运动情况，依据修正过的地震动平稳自功率谱方程，对其进行数值变换后，求解其微分方程组，得到两端自由滑动的应力功率谱密度方程，分析得知该方程与振型函数有关。选取特定管道参数和相关计算参数，分析地震管道在硬土和软土两种情况下，管中应力和位移的变化情况。结果表明，管道中部位移和应力趋于恒定，应力和位移变化主要发生在边界处，横向振动的最大应力发生在滑动边界上。

对于地震管道的平稳随机振动，管道和地面横向和纵向运动情况完全不同，而且非常复杂，纵向运动对埋地管道横向运动的分析结果有影响。因此，该计算结果是在作了多次假设的情况下得到的，具有参考性和实用性。

［1］杨其伟，屈铁军，林锋.地震作用下埋地管线轴线随机反应[J].北方工业大学学报，2004（01）:37-41.

［2］孙宁，李瑰贤.随机振动信号的一种简单模拟计算方法[J].振动与冲击，2000(02)：50-51.

［3］陈学前，冯加权，杜强.随机振动数值仿真中基础激励的自动反馈识别[J].力学与实践，2006(05):47-49.

［4］郭恩栋，冯启民.跨断层埋地钢管道抗震计算方法研究[J].地震工程与工程振动，1999（04）:64-66.

［5］孙建刚，薛景宏，王振.地下输液管道动力反应分析[J].地震工程与工程振动，2000（11）:54-56.

［6］滕振超.跨越管道地震响应分析及基于性能的抗震设计[D].大庆：大庆石油学院，2003.

［7］屈铁军，王前信.地下管线在空间随机分布的地震作用下的反应[J].工程力学，2003(03):55-57.

［8］薛景宏，朱福祥，张永益.土特性改变对埋地管线轴向地震响应的影响[J].大庆石油学院学报，2001(02):37-39.

［9］朱学旺，刘青林.随机振动载荷动力学等效的一种工程实现方法[J].实验力学,2007(06):568-574.

［10］范么清，楼梦麟，毛巍.非线性单自由度复合随机振动的蒙特卡罗模拟[J].武汉理工大学学报,2008(01):67-70.

［11］帅健.管线力学[M].北京：科学出版社，2010：219-222.

［12］潘无名，杨明举，徐扬.随机振动系统构件应力谱密度的计算[J].西南交通大学学报，2003(01):12-16.

［13］帅健，吕英民，蔡强康.埋地管道的平稳随机振动[J].石油大学学报(自然科学版)，1999(04):65-70.

［14］周建，王前信.地下管道随机反应及动力可靠性分析[J].土木工程学报，1993(04):54-60.

［15］帅健，许葵.埋地管道随机振动的摄动分析[J].力学季刊，2003(06):244-249.

Horizontal Stationary Random Vibrations of Earthquake Pipelines

RAN Longfei1，WANG Tianqun2
(Liaoning Shihua University,Fushun 113001，Liaoning,China)

According to influence degree of earthquake action on the buried pipelines,applying the method of numerical calculation to obtain analytic solutions of vibration mode function.Stationary random vibrations of buried pipeline in the calculation method of hypothesis is linear vibration problem,has zero mean and response pipe soil system incentive,co-variance function and correlation function to get is the same.According to the analytic solution for buried pipeline stationary vibrationsolution,lateral vibration analysis of pipeline.The results show that:the horizontal vibration of the pipeline,the central stress and displacement tends to a constant,the boundary region of the stress and displacement change,the lateral ride vibration of buried pipeline in the maximum stress occurs in the slip boundary.

earthquake;pipeline;numerical calculation;vibration;analytic solution

TE973.1

B

1001－3938（2015）06-0026-03

冉龙飞（1989—），男，陕西宝鸡人，硕士，主要从事油气储运系统的安全工作。

2015-03-17

罗 刚