测地曲率计算公式的推导方法

测地曲率计算公式的推导方法

邢家省1，白璐1，罗秀华2

(1.北京航空航天大学数学与系统科学学院，数学、信息与行为教育部重点实验室,

北京 100191;2.平顶山教育学院，河南 平顶山 467000)

摘要：考虑曲面上曲线测地曲率计算公式的推导问题，运用向量的外积运算，给出了直接推导的计算公式；在曲面正交曲线坐标网下，给出测地曲率计算公式的2种来源过程，并由此得出Liouville公式的推导方法.

关键词：测地曲率;正交曲线；坐标网；Liouville公式

文章编号：1007-2985(2015)05-0007-06

收稿日期：2015-05-13

基金项目：国家自然科学基金资助项目(11201020)；北京航空航天大学校级重大教改项目(201401)

作者简介：邢家省(1964—),男,河南泌阳人,北京航空航天大学副教授，博士,主要从事偏微分方程和微分几何研究.

中图分类号：O186.1文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.05.002

关于曲面上曲线测地曲率的计算公式，文献[1]中采用的是利用曲面论基本方程给出的推导过程，需要准备的知识较多，证明过程相当繁杂；文献[2-6]中在曲面正交曲线坐标网下，给出测地曲率计算的Liouville公式[1-7]的直接证明.笔者运用向量的外积运算法则，就可以直接给出测地曲率的计算公式.在正交曲线坐标网下，给出了推导测地曲率的简化公式的2种过程，并指出Liouville 公式的2种来源，利用直接方法给出测地线方程的最终形式.

1　曲面上曲线测地曲率的定义

设曲面Σ的参数方程为Σ:r=r(u,v),(u,v)∈Δ.若r(u,v)具有二阶连续偏导数，且ru×rv≠0，称则曲面Σ为C2类的正则曲面.现在任固定曲面Σ上一点P(u,v)，并设TP为曲面Σ在P点的切平面.

曲线Γ：r=r(u(s),v(s))是Σ上过P点的一曲线，其中s是曲线的自然参数.设n为曲面Σ在P点的单位法向量，以α表示曲线Γ上P点处的单位切向量，以β表示曲线Γ上P点处的主法向量，γ是副法向量.

定义1 [1-9]曲面Σ上，曲线Γ在P点的单位切向量的导向量α′(s)在切平面TP上的投影向量为τP=α′(s)-(α′(s)·n)n，称为曲线Γ在P点的测地曲率向量.

称Dα=dα-(dα·n)n为切向量场α(s)沿曲线Γ的绝对微分.由α′(s)=r″(s)，故有τP=r″(s)-(r″(s)·n)n .显然 α′(s)-(α′(s)·n)n与n,α都垂直.命 ε=n×α，则α,ε,n是彼此正交的单位向量，并且构成一右手系，α′(s)-(α′(s)·n)n平行于ε.α′(s)在切平面TP上的投影向量也就是α′(s)在ε上的投影向量.

定义2 [1-9]曲面Σ上，曲线Γ的切向量的导向量α′(s)在ε上的投影向量为τP=(α′(s)·ε)ε，称为曲线Γ在P点的测地曲率向量.

显然有τP=α′(s)-(α′(s)·n)n，τP=(α′(s)·ε)ε，τP=(r″(s)·ε)ε .

定义3 [1-9]将r″(s)·ε称为曲线Γ在P点的测地曲率，记作kg，kg=r″(s)·ε .

显然kg=(r′(s),r″(s),n(s)) ，kgε=r″(s)-(r″(s)·n)n.

2　曲面上曲线测地曲率的一般计算公式的直接推导方法

设Γ是曲面Σ上的一条曲线，其参数方程为u1=u1(s),u2=u2(s),或r=r(u1(s),u2(s))=r(s)，这里s是该曲线的自然参数.

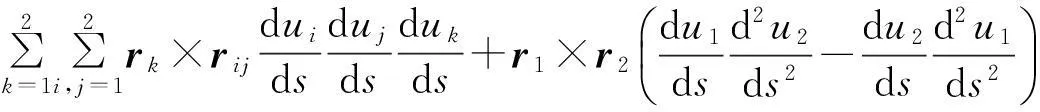
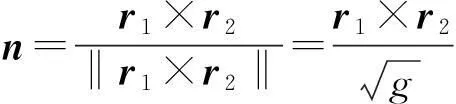
(rk×rij)·(r1×r2)=(rk·r1)(rij·r2)-(rk·r2)(rij·r1)=gk1(rij·r2)-gk2(rij·r1).

代入测地曲率的计算公式，得

(1)

(1)式是测地曲率的一般计算公式，方便于直接使用.

这里仅用向量外积运算法就给出了测地曲率的一般计算公式，与利用曲面论的基本方程式[1-4]推导出测地曲率的计算公式是一致的.

3　正交坐标曲线网下测地曲率的计算公式

当曲面r=r(u1,u2)上的坐标曲线构成正交网时，有 r1·r2=0，gij=ri·rj,g12=g21=0，g=g11g22.注意到

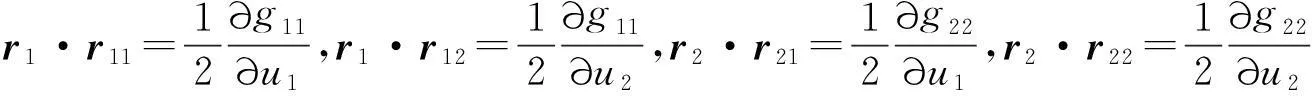
代入测地曲率的一般计算公式(1)中，整理后得

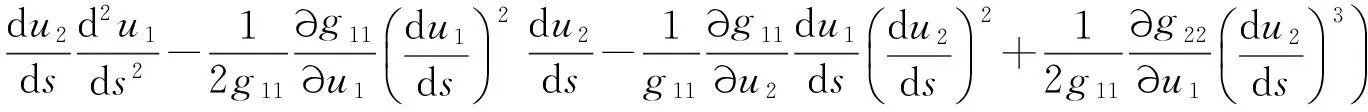
对于曲面r=r(u,v)上的坐标曲线构成正交网时，有E=g11,G=g22,F=g12=0，u=u1,v=u2.从而有如下结论成立：

定理1 [1,7-8]设曲面Σ:r=r(u,v)上的坐标曲线构成正交网，Γ是曲面Σ上的一条曲线，其参数方程为u=u(s),v=v(s),或r=r(u(s),v(s))=r(s)，这里s是该曲线的自然参数，则曲线Γ的测地曲率为

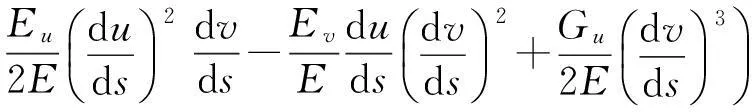
(2)

4　正交坐标曲线网下测地曲率的推导过程

定理2 [1,7-8]设曲面Σ:r=r(u,v)上的坐标曲线构成正交网，Γ是曲面Σ上的一条曲线，其方程为r=r(u(s),v(s))，这里s是该曲线的自然参数，则曲线Γ测地曲率为

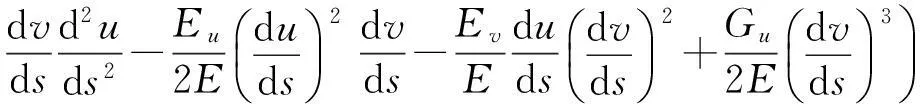
(3)

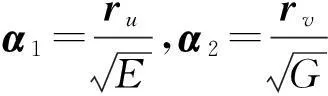
对r=r(s)=r(u(s),v(s))直接求导，得

(4)

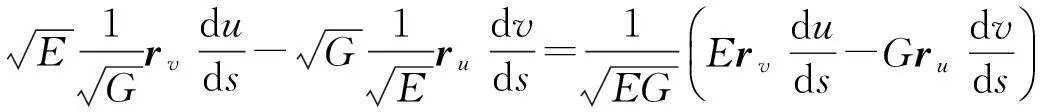
(5)

将(4)，(5)式代入测地曲率的计算公式，得到

(6)

利用ru·ru=E，ru·rv=0，rv·rv=G，可得

(7)

将(7)式各项代入(6)式中，得

这正是(3)式的结果[8].

5　正交坐标曲线网下测地曲率的Liouville公式

设曲面r=r(u,v)上的坐标曲线构成正交网. 令曲面上曲线r=r(s)=r(u(s),v(s))的切方向与ru的夹角为θ，则有

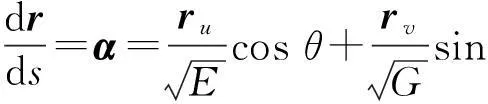
(8)

又

(9)

比较(8)，(9)式，得

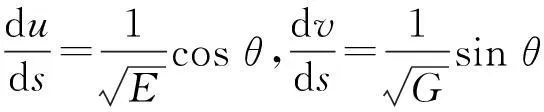
(10)

所以有

(11)

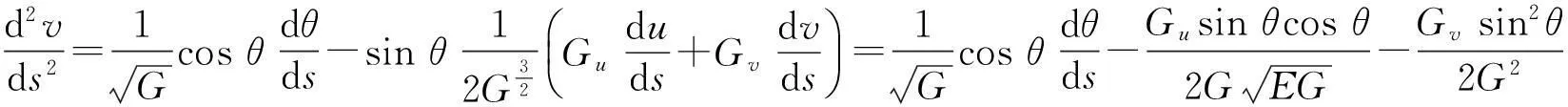
(12)

将(10)至(12)式代入(2)式，或者(3)式中，整理后得

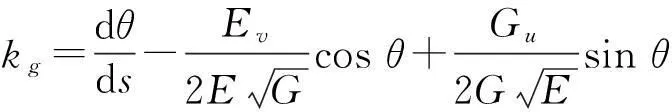
(13)

(13)式称为刘维尔(Liouville )公式[1,7]，可用于计算测地曲率和求解曲面上的测地线方程[1-6]，推导高斯-波涅公式[2-6]也用到(13)式.在文献[2-6]中，给出了另一种推导方法.

例1 [1,10]如果在曲面上引进半测地坐标网ds2=du2+G(u,v)dv2，求证：

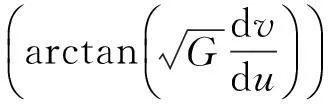
证明由题设，E= 1，F= 0，G=G(u;v)，代入Liouville公式，得

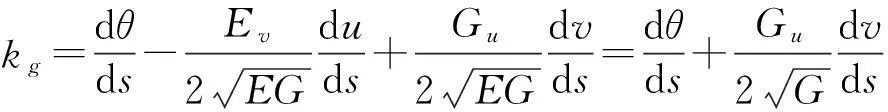
所以，

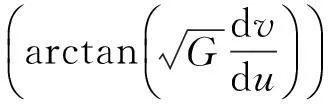
6　测地线的方程的最终显式表示形式

对曲面Σ:r=r(u,v)，设Γ:r=r(s)=r(u(s),v(s))是曲面Σ上的测地线，s是曲线的自然参数.

曲线Γ:r=r(s)=r(u(s),v(s))是测地线的充分必要条件为[8-9]r″(s)·ru=0,r″(s)·rv=0 .

由于

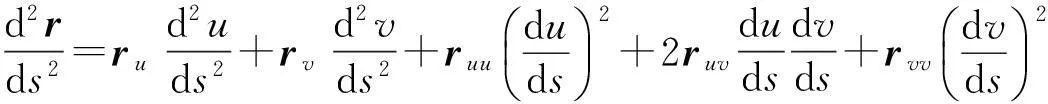
(14)

将(14)式分别与ru,rv作内积，得

于是有

(15)

通常将(15)式改写为如下的等价形式：

(16)

(16)式就是一般参数曲面上的测地线的方程，这里给出了直接的推导过程.利用(16)式可证明测地线的存在唯一性定理，求解曲面上的测地线方程及理论推导.

特别地，当曲面r=r(u,v)上的坐标曲线构成正交网时，有ru·rv=F=0，此时曲面上的曲线为测地线的充分必要条件为[8]

(17)

(17)式可用于求解正交网下曲面上测地线的方程[8].

参考文献：

[1]梅向明，黄敬之.微分几何[M].第4版.北京：高等教育出版社出版，2008：82-84；146-149.

[2]苏步青，胡和生，沈纯理,等.微分几何[M].北京：人民教育出版社，1980：197-203.

[3]陈维桓.微分几何[M].北京:北京大学出版社,2006：139-143；229-241.

[4]彭家贵，陈卿.微分几何[M].北京：高等教育出版社，2002：43-47；110-117.

[5]王幼宁，刘继志.微分几何讲义[M].北京：北京师范大学出版社,2003：149-153.

[6]陈维桓.微分几何例题详解和习题汇编[M].北京：高等教育出版社出版,2010：171-219.

[7]邢家省,张光照.曲面上曲线的测地曲率向量的注记[J].吉首大学学报：自然科学版，2013，34(4)：7-10.

[8]JOHNOPREA.DifferentialGeometryandItsApplications[M].北京：机械工业出版社，2005：223-242.

[9]邢家省，高建全，罗秀华.曲面上测地线和短程线的性质[J].四川理工学院学报：自然科学版，2015,28(1)：63-66.

[10]梅向明，王汇淳.微分几何学习指导与习题选解[M].北京：高等教育出版社,2004：189-190.

Derivation of Calculation Formula of Geodesic Curvature

XING Jiasheng1，BAI Lu1，LUO Xiuhua2

(1.Department of Mathematics,LMIB of the Ministry of Education,Beihang University,Beijing 100191，China;

2.Pingdingshan Institute of Education,Pingdingshan 467000,Henan China )

Abstract:The derivation of the calculation formula of geodesic curvature on curved surface is discussed in this paper.The directly derived calculation formula is obtained by means of vector outer product.Two derivation processes of the calculation formula of geodesic curvature and the derivation of the Liouville formula are demonstrated in the coordinate grid of the orthogonal curve.

Key words:geodesic curvature;orthogonal curve;coordinate grid；Liouville formula

(责任编辑向阳洁)