一阶常系数非奇次线性微分方程的通解

一阶常系数非奇次线性微分方程的通解

邓雪1，赵俊峰2，张雄锋3

(1.华南理工大学数学学院，广东 广州 510640；2.广东工贸职业技术学院机械工程系，

广东 广州 510510；3.华南理工大学物理与光电学院，广东 广州 510640)

摘要：通过严谨的数学推导，利用待定系数法，对于一阶常系数非奇次线性微分方程y′+py=Q(x)，给出了Q(x)的不同情况的特解的具体表达式，以及带有不同表达形式的特解的通解公式.

关键词：通解；特解；线性微分方程；待定系数法

文章编号：1007-2985(2015)05-0013-03

收稿日期：2015-04-07

基金项目：教育部人文社会科学规划

作者简介：邓雪(1974—)，女，辽宁沈阳人，华南理工大学数学学院副教授，博士，主要从事高等数学研究.

中图分类号：O172文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.05.003

1　问题的提出

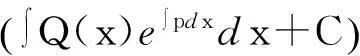
2　主要结果

定理1对于一阶常系数非奇次线性微分方程y′+py=Q(x)，其中p为常数，Q(x)已知，根据Q(x)的不同情况，对应特解的具体表达式为：

(1)

证明针对一阶常系数非奇次线性微分方程

y′+py=Q(x)，

(2)

用待定系数法求其对应的非齐次的特解.现考虑3种情况：

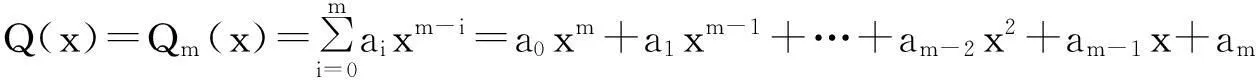
(3)

则

(4)

将(3)，(4)式代入(2)式中，有

mb0xm-1+ (m-1)b1xm-2+…+2bm-2x+bm-1+pb0xm+pb1xm-1+…+

pbm-2x2+pbm-1x+pbm=a0xm+a1xm-1+…+

am-2x2+am-1x+am.

(5)

比较(5)式两端同类项的系数得

(6)

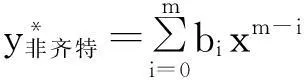
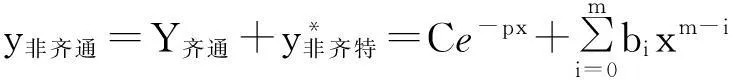
(7)

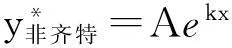
(8)

aAcosax-aBsinax+pAsinax+pBcosax=λsinax+γcosax，

进而得

(9)

综上所述，由(7)，(8)，(9)式，推导出(1)式.证毕.

3　应用

例1求方程3y′+2y=6x的通解.

3b0+2b0x+2b1=6x.

(10)

比较(10)式两端同类项的系数得

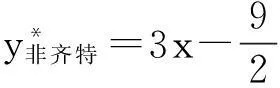
例2求方程y′+2y=5e2x的通解.

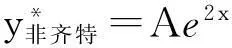
2Ae2x+2Ae2x=5e2x.

(11)

例3求方程y′+y=sinx的通解.

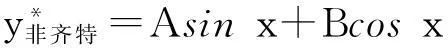
(Acosx-Bsinx)+(Asinx+Bcosx)=sinx，

整理得

(A-B)sinx+(A+B)cosx=sinx.

(12)

比较(12)式两端同类项的系数得

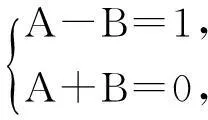
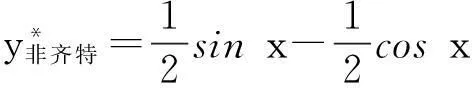
4　结语

针对Q(x)的不同情况，利用待定系数法推导出一阶常系数非奇次线性微分方程y′+py=Q(x)的通解的具体表达式.同时，通过实例验证这一结果是有效的.在实际教学中，这一结论为讲授“一阶常系数非奇次线性微分方程”的教师和学习该课程的学生扩展了思路，同时在求解过程中省去了繁琐的计算.

参考文献：

[1] 同济大学应用数学系.高等数学(下)[M].北京：高等教育出版社，2002.

[2] 王全迪，郭艾，杨立洪.高等数学(下)[M].北京：高等教育出版社，2009.

[3] 陈凤平，付一平，杨立洪.高等数学(下)[M].广州：华南理工大学出版社，2005.

[4] 王丽燕.高等数学大讲堂[M].大连：大连理工大学出版社，2004.

[5] 黄庆怀.2012考研高等数学辅导教材[M].北京：北京航空航天大学出版社，2011.

General Solutions of One Order Constant Coefficient

Non-Homogeneous Linear Differential Equation

DENG Xue1,ZHAO Junfeng2,ZHANG Xiongfeng3

(1.School of Mathematics,South China University of Technology,Guangzhou 510640,China;2.Department of Mechanical

Engineering,Guangdong College of Industry and Commerce,Guangzhou 510510,China;3.School of Physics and

Photoelectricity,South China University of Technology,Guangzhou 510640,China)

Abstract:For one order constant coefficient non-homogeneous linear differential equation y′+py=Q(x),the concrete expression of special solution with different situations of Q(x) is given through the undetermined coefficient method.The general solution formula with special solution of different expression is presented as well.

Key words:general solution;special solution;linear differential equation;undetermined coefficient method

(责任编辑向阳洁)