改进的最近电平逼近调制策略在模块化多电平变流器中的应用

肖　浩，　高桂革，　曾宪文，　裴泽阳

(上海电机学院 电气学院， 上海 200240)



改进的最近电平逼近调制策略在模块化多电平变流器中的应用

肖浩，高桂革，曾宪文，裴泽阳

(上海电机学院 电气学院， 上海 200240)

摘要:介绍了在最近电平逼近(NLM)调制方式下模块化多电平变流器(MMC)的拓扑结构及其工作原理，指出当模块化变流器子模块数较少时输出波形含有较大的谐波分量；研究了一种改进的NLM调制策略，通过改变传统取整函数增加了输出调制正弦波形电平数，减小了输出电压波形的谐波含量，改善了输出波形质量；分析了不同取整函数对输出波形质量的影响。最后通过MATLAB/Simulink软件仿真验证了该策略的有效性。

关键词：模块化多电平变流器； 最近电平逼近； 谐波； 取整函数

海上风能以其资源丰富，风能利用率高以及不占用陆上土地资源等优势而得到迅速发展。截止到2012年，欧洲新增风力装机容量为1.2744GW，其中，陆上风电为1.0729GW，海上风电为1.166GW。海上风电的市场较2011年新增了35%。此外，中国规划到2015年和2020年，海上风电总装机将分别累计达到5GW和30GW[1-3]。随着海上风电的不断发展，海上风电场并网的柔性直流输电系统(Voltage Source Converter Based High-Voltage Direct Current, VSC-HVDC)也越来越受到业界的关注。

VSC-HVDC常用的电压源换流器有两电平换流器、二极管箝位型三电平换流器、模块化多电平换流器(Modular Multilevel Converter, MMC)[1]。MMC以其自身拓扑结构特别适合于VSC-HVDC系统。业界学者对其调制方式也有大量的研究。文献[3]中提出了适用于MMC的改进载波相移调制方式。该调制方式适合低电平水平下运行，且在消除换流器低次谐波上具有明显优势，但在子模块数较多时控制过程显得十分复杂。文献[4]中提出了一种新颖的适用于MMC的载波移相调制方式，该方式动态调节能力强，具有良好的谐波特性，但高频脉冲宽度调制运行损耗大。文献[1，5]中分析了MMC不同调制方式的特点，总结了它们各自的优缺点，指出最近电平逼近(Nearest Level Modulation, NLM)调制方式可避免高频PWM调制，且方法简单，较适用于MMC；缺点是在输出电平数较少的情况下，输出波形谐波含量会升高。文献[2]中提出了一种改进的NLM，但没有分析取整函数的改变对整个MMC运行的影响以及改进后子模块电压有效值的变化。

本文针对NLM调制策略下的MMC在子模块数较少时输出电压谐波含量高的缺点，研究了一种改进的NLM调制策略，针对文献[2]中分析不全面、不具体的部分做了进一步地分析与证明，最后使用MATLAB/Simulink仿真验证了该策略的有效性。

1MMC基本原理

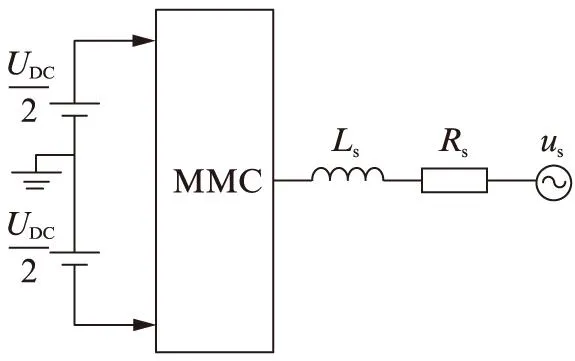
单相(以A相为例)MMC的拓扑结构如图1所示，每一相有上、下两个桥臂，每个桥臂有N个子模块SM1~SMn；上、下桥臂之间串联两个限流电抗器。每个子模块由2个开关器件、2个反并联二极管、1个稳压电容组成。

图1　单相MMC拓扑结构Fig.1　Single-phase MMC topology

根据基尔霍夫电压定律以及基尔霍夫电流定律可知[5-8]：

(1)

(2)

式中，ua为MMC输出电压;uU和uL分别为上、下桥臂输出电压;L为限流电抗器电感值;UDC为直流母线电压;idiff为同时流过上、下桥臂换流器的内部电流。联立式(1)、(2)可得

(3)

定义

(4)

故可得

(5)

(6)

式中，m为MMC输出电压调制比；ω为电网电压旋转角速度。

由于Ldidiff/dt的大小与桥臂电流中交流、直流环流分量有关，与桥臂电流中的相电流分量无关，且在系统正常运行时其数值不大，故在研究MMC与外部交流系统的相互作用时可以忽略其影响[4]，得到

(7)

正常运行时在一个开关周期内会开通N个子模块，可得每个子模块电容电压为

(8)

式中，ud为每个子模块电容电压有效值。

2传统NLM调制策略

NLM调制方式的本质在于任意时刻投入若干个子模块构成的方波尽可能逼近于调制波。随着调制波瞬时值从零不断增大，单相下桥臂投入的子模块也不断增多，而上桥臂投入的子模块数随之减少，使输出波电压跟随调制波升高。在每个开关周期内上、下桥臂需要投入子模块数量为[9-13]：

(9)

式中，roundx[f(x)]为就近取整函数。

根据式(5)、(9)得到NLM正弦调制电压为

(10)

在传统控制策略下roundx中x的取值为0.5。若f(x)为正数，且其小数部分大于0.5，则取与之数轴上向右靠近的整数；若f(x)的小数部分小于0.5时，则取与之数轴上向左靠近的整数。若f(x)为负数，且其小数部分大于0.5，则取与之数轴上向左靠近的整数；若f(x)的小数部分小于0.5时，则取与之数轴上向右靠近的整数。以N=16，UDC=40kV为例，图2给出了x=0.5时，传统MMC的NLM调制过程。

图2　x=0.5时传统MMC的NLM调制Fig.2　Traditional NLM modulation of MMC when x=0.5

由式(9)可得到上、下桥臂需要开通的子模块个数，然后根据桥臂电流方向和桥臂电容、电压的大小选择得到开通相应子模块的脉冲信号，最终得到NLM的调制信号[9-10]。

3改进的NLM调制策略

文献[2]中仅分析比较了当x=0.25和x=0.5时的传统NLM控制情况，仅分析了当x=0.25时MMC增加以及输出波形质量的提高，没有考虑改进后对子模块稳定电压有效值的影响，也未考虑其他x取值与MMC输出调制电压、正弦调制电压之差的关系。本文将数学推导证明任意改变传统x的取值都将使MMC输出电平增加，然后完成了对改进后模块电压有效值的估算，并分析MMC输出调制误差与x的关系。

3.1　MMC输出调制波形特性分析

图3给出了x=0.4时MMC的NLM正弦调制电压波形。

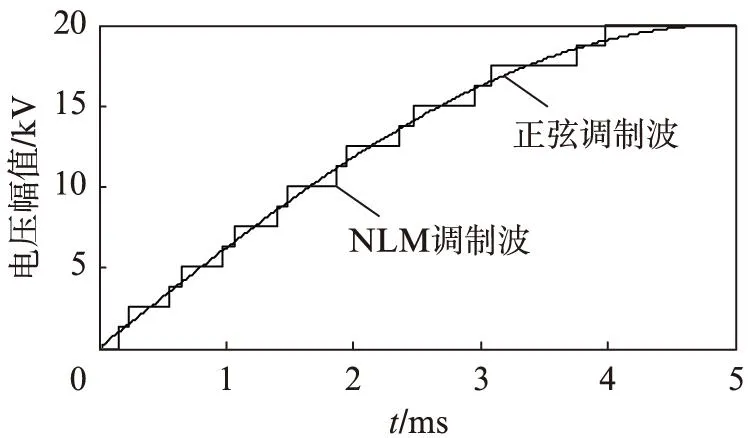
图3　x=0.4时MMC的NLM调制Fig.3　NLM modulation of MMC when x=0.4

在其他条件不变的情况下，图2输出的NLM正弦电压波在半个周期内的电平数为17，图3输出的电平数为33，几乎是图2的2倍，输出波形也更加趋近于正弦调制波。

根据式(9)可以得到上、下桥臂调制电压为

(11)

同样以N=16，UDC=40kV，调制比为1的情况为例，在1/4周期内,可以得到当x=0.5和x=0.4时,上、下桥臂NLM调制电压输出波形，如图4所示。

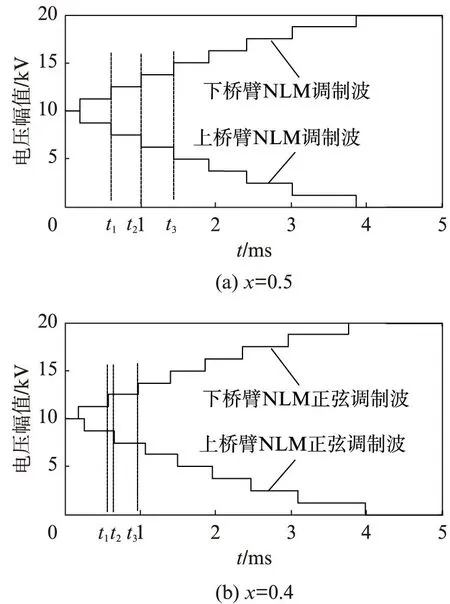
图4　x=0.5和x=0.4时上、下桥臂输出的调制电压波Fig.4　 Waveforms of modulation voltage output from upper and lower arms when x=0.4 and x=0.5

图4(a)和(b)唯一区别在于： 由于x的取值不同，导致电平产生时间不同，图4(a)中产生的上、下桥臂NLM调制电压基本对称，而图4(b)中很明显不对称。

由图4(a)可见，当x=0.5时,任取两个时间段t1~t2，t2~t3。假设在t1~t2内下桥臂子模块开通个数为M，则上桥臂的子模块开通个数为N-M，可得

(12)

u=(M-0.5N)ud

(12)

u=(M-0.5N)ud

(13)

分析t2~t3内调制输出电压波形，可得到t1～t2内下桥臂子模块开通个数为M+1，则上桥臂子模块开通个数为N-M-1，可得

(14)

u=(M-0.5N+1)ud

(14)

u=(M-0.5N+1)ud

(15)

则式(15)减去式(13)得到

|Δu|=ud

(16)

由上述分析可知，在相邻两个时间段内采用传统NLM策略时MMC输出调制电压跳变为ud。

由图4(b)可见，当x=0.4时,任取两个时间段t1~t2，t2~t3。在t1~t2内，假设下桥臂的子模块开通个数为M+1，则上桥臂的子模块开通个数为N-M，可得

(17)

u=(M-0.5N+0.5)ud

(17)

u=(M-0.5N+0.5)ud

(18)

分析t2~t3内调制输出电压波形可得到在t2~t3内桥臂的子模块开通个数为M+1，则上桥臂的子模块开通个数为N-M-1，可得

(19)

u=(M-0.5N+1)ud

(19)

u=(M-0.5N+1)ud

(20)

则式(20)减去式(18)可得到

|Δu|=0.5ud

(21)

由上述分析可知，在相邻两个时间段内，x=0.4时MMC输出调制电压跳变为0.5ud，分析比较式(16)和式(21)，可得到在相同的正弦调制电压幅值范围内,x=0.4时输出电压跳变幅值为传统的1/2。很显然，并不是只有在文献[2]中x=0.25时才会出现MMC输出电平数增加100%的情况。应当指出，只要当x≠0.5，即传统NLM策略时，均会出现MMC输出电平数增加100%的情况。

3.2　改进后子模块电压有效值估算

当x=0.4时，由于上、下桥臂的子模块调制电压跳变的时刻不同，导致t1~t2内投入的上、下桥臂子模的块总数为N+1。分析可知，x在0~0.5内,随着其数值增大，子模块投入总数为N所占的时间会越来越长 。按照有效电压的观点，子模块电压有效值也会越来越接近ud，当x逐渐趋近于0时，子模块有效值越接近Nud/(N+1)。由于当N达到一定数量时，改进前、后的子模块电压有效值变化并不大，在实际计算时可以将改进后的子模块有效值取其随x变化的最大值和最小值得到它们的平均值，故得到改进后的子模块有效电容电压为

(22)

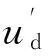
3.3　MMC输出调制误差与x的关系分析

传统NLM调制策略将MMC输出的调制电压与正弦调制电压之差控制在±ud/2以内。任意取两个相邻时刻t1与t2，在t1时刻，由式(9)可知

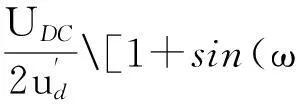
(23)

由式(23)可得

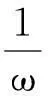
(24)

由式(18)可知，在t1时刻MMC输出调制电压为

(25)

在t1的前一时刻MMC输出NLM调制电压则为

(26)

将式(24)代入式(6)可得到t1时刻正弦调制电压为

(27)

式(25)减去式(26)，得到

(28)

式(26)减去式(27)得到

(29)

MMC输出调制电压与正弦调制电压之差满足

Δu=max{Δu1,Δu2}

(30)

即得到Δu与x之间的关系为

(31)

按照上述推导，在t2时刻得到的Δu与x之间的关系，本文不再赘述。

本文仅分析了0

(32)

由式(31)和式(32)可知，当x=0.25和x=0.75时，MMC输出NLM调制电压与正弦调制电压之差可取得最小值，为ud/4，且x的取值偏离0.25和0.75越大，则MMC输出的电压与调制波电压之差越大。

4仿真分析

为了验证改进策略的有效性，本文在MATLAB/Simulink仿真软件下搭建了单相MMC仿真模型，如图5所示，仿真参数如表1所示[2]。

图5　单相MMC仿真模型Fig.5　Single-phase MMC simulation model

表1　系统仿真参数Tab. 1　Simulation parameters

图6、7分别给出了x=0.5、0.25时的MMC输出交流电压波形及其频谱分析图。图8给出了x=0.5、0.25时上桥臂16个子模块的输出电压波形。

由图6、7可见，x=0.25时的输出波形较x=0.5时更接近于正弦波，且当x=0.25，其输出电压谐波含量为1.02%，明显低于x=0.5时的1.98%。

图6　x=0.5和x=0.25时的MMC输出电压波形Fig.6　 MMC output voltage waveform when x=0.5 and x=0.25

图7　 x=0.5和x=0.25时的MMC输出 电压波形频谱分析Fig.7　 Spectral analysis of MMC output voltage waveform when x=0.5 and x=0.25

由图8可见，当x=0.5时，其电容电压约为2.5kV；x=0.25时，其有效值约为2.43kV，这是由于子模块在运行过程中必然存在电压波动，但电压的波动不大，从而验证了本文提出结论。

图8　x=0.5和x=0.25时MMC子模块输出电压波形Fig.8　 Waveforms of MMC sub-module output voltage when x=0.5 and x=0.25

表2给出了x为0.05~0.95，间隔0.05时输出波形的谐波含量。由表2可见，输出波形的谐波含量以x=0.5为分界线对称分布，且x的取值越靠近0.25和0.75，谐波含量越少，x=0.5时谐波含量最高，进一步验证了本文改进策略的有效性。

表2　MMC输出谐波含量与x值关系Tab.2　 Relationship between MMC output harmonic content and the value of x

5结语

本文研究了一种MMC改进的NLM调制策略，提出任意改变x的取值可以增加近100%的MMC输出电平数的结论，并进行了数学公式推导。同时，通过数学推导找出了MMC输出调制电压与正弦调制波电压之差与x之间的关系，得到只有当x的取值越接近0.25以及0.75时，MMC输出的电压与调制波电压之差最小，且偏离0.25和0.75越大，MMC输出调制电压与正弦调制波电压之差越大，MMC输出电压谐波含量越高。最后通过MATLAB/Simulink仿真验证了该改进策略的有效性。

参考文献：

[1]王志新,吴杰,徐烈,等.大型海上风电场并网VSC_

HVDC变流器关键技术[J].中国电机工程学报,2013,33(19)： 14-27.

[2]Hu Pengfei,Jiang Daozhuo.A level-increased nearest level modulation methodfor modular multilevel converters[J].IEEE Transactions on Power Electronics,2015,30(4): 1836-1842.

[3]赵昕，赵成勇，李广凯，等.采用载波移相技术的模块化多电平换流器电容电压平衡控制[J].中国电机工程学报，2011,31(21)： 48-55.

[4]屠卿瑞.模块化多电平换流器型直流输电若干问题的研究[D].杭州：浙江大学，2013： 38-58.

[5]徐政.柔性直流输电系统[M].北京：机械工业出版社,2014： 33-42.

[6]Solas E,Abad G,Barrena J A.Modulation of modular multilevel converter for HVDC application[C]∥International Power Electronics and Motion Control Conference.Ohrid,Macedonia：IEEE,2010： T284-T289．

[7]张明.模块化多电平变换器的控制策略[D].杭州：浙江大学.2014： 11-13.

[8]黄川.海上风电场VSC_HVDC柔性直流输电变流器研究[D].上海：上海交通大学.2011： 53-61.

[9]Du Sixing Liu Jinjun,Liu Teng.Modulation and closed-loop-based DC capacitor voltage control for MMC with fundamental switching frequency[J].IEEE Transactions on Power Electronics,2015,30(1)： 327-338.志新,吴杰,徐烈,等.大型海上风电场并网VSC_

HVDC变流器关键技术[J].中国电机工程学报,2013,33(19)： 14-27.

[2]Hu Pengfei,Jiang Daozhuo.A level-increased nearest level modulation methodfor modular multilevel converters[J].IEEE Transactions on Power Electronics,2015,30(4): 1836-1842.

[3]赵昕，赵成勇，李广凯，等.采用载波移相技术的模块化多电平换流器电容电压平衡控制[J].中国电机工程学报，2011,31(21)： 48-55.

[4]屠卿瑞.模块化多电平换流器型直流输电若干问题的研究[D].杭州：浙江大学，2013： 38-58.

[5]徐政.柔性直流输电系统[M].北京：机械工业出版社,2014： 33-42.

[6]Solas E,Abad G,Barrena J A.Modulation of modular multilevel converter for HVDC application[C]∥International Power Electronics and Motion Control Conference.Ohrid,Macedonia：IEEE,2010： T284-T289．

[7]张明.模块化多电平变换器的控制策略[D].杭州：浙江大学.2014： 11-13.

[8]黄川.海上风电场VSC_HVDC柔性直流输电变流器研究[D].上海：上海交通大学.2011： 53-61.

[9]Du Sixing Liu Jinjun,Liu Teng.Modulation and closed-loop-based DC capacitor voltage control for MMC with fundamental switching frequency[J].IEEE Transactions on Power Electronics,2015,30(1)： 327-338.

[10]管敏渊,徐政,屠卿瑞,等.模块化多电平换流器型直流输电的调制策略[J].电力系统自动化,2010,34(2)： 48-52.

[11]Peralta J,Saad H,Dennetiere S,et al Detailed and averaged models for a 401-level MMC-HVDC system[J].IEEE Transactions on Power Delivery,2012,27(3)： 1501-1508．

[12]王国强,王志新,李爽.模块化多电平变流器的直接功率控制仿真研究[J].中国电机工程学报,2012,32(6)： 64-71.

[13]屠卿瑞,徐政,郑翔,等.模块化多电平换流器型直流输电内部环流机理分析[J].高电压技术,2010,36(2)： 547-552.敏渊,徐政,屠卿瑞,等.模块化多电平换流器型直流输电的调制策略[J].电力系统自动化,2010,34(2)： 48-52.

[11]Peralta J,Saad H,Dennetiere S,et al Detailed and averaged models for a 401-level MMC-HVDC system[J].IEEE Transactions on Power Delivery,2012,27(3)： 1501-1508．

[12]王国强,王志新,李爽.模块化多电平变流器的直接功率控制仿真研究[J].中国电机工程学报,2012,32(6)： 64-71.

[13]屠卿瑞,徐政,郑翔,等.模块化多电平换流器型直流输电内部环流机理分析[J].高电压技术,2010,36(2)： 547-552.

Modified Nearest Level Modulation for Modular Multilevel Converter

XIAOHao，GAOGuige，ZENGXianwen，PEIZeyang

(School of Electrical Engineering, Shanghai Dianji University, Shanghai 200240, China)

Abstract:This paper briefly introduces the topology of modular multilevel converters and its operation principle in nearest level modulation. It is pointed out that the output waveform contains large harmonic components when the modular multilevel converter has less sub-modular. An improved nearest level modulation strategy is proposed. By changing the traditional rounding function to increase the output level number of modulating sine waves to reduce harmonics in the output voltage and improve the output waveform. The effects of different rounding function on the output waveform quality are analyzed. Simulation results verify effectiveness of the strategy.

Key words:modular multilevel converter (MMC); nearest level modulation (NLM); harmonic; rounding function

文章编号2095-0020(2015)02-0077-05

作者简介:侯培红(1959-)，男，教授，博士，主要研究方向为机械设计制造、硬材料及其加工、数控加工技术，E-mail： peihonghou5@163.com

基金项目：上海电机学院重点学科资助项目(12XKJ01)；上海市闵行区校企合作资助项目(14Q12)

收稿日期：2015-03-09

中图分类号:TM 464.23

文献标志码:A