岩石可钻性及岩石破碎机理探讨
吴其干
(广东省有色金属地质局九三一队,广东汕头515041)
岩石可钻性及岩石破碎机理探讨
吴其干*
(广东省有色金属地质局九三一队,广东汕头515041)
目前的岩石可钻性分级与实际的钻进时效有出入,相应的岩石在压头下破碎机理的观点也很难解析破碎坑的顶角和大小问题,通过进一步的探讨和计算,做出了岩石在压头下破碎机理的推论,并对岩石可钻性的划分提出了建议。
可钻性;破碎机理;探讨
通常在选用钻头及选择钻压等钻进参数时,主要以岩石的可钻性等级为依据,而岩石的可钻性等级则主要根据压入硬度的大小进行划分,但在实际岩芯钻探过程中,往往会发现实际的钻进时效与预计钻进时效差别很大,例如压入硬度相差不大的黑云母花岗岩(462kg/mm2)和灰白色颗粒石英砂岩(471kg/mm2)钻进的实际时效分别为1.97m/h、0.63m/h,差别很大。可见目前岩石的可钻性等级分类不太合理,需进一步探讨。了解和掌握岩石在压模作用下破碎机理将有助于我们更合理地划分岩石的可钻性等级。
目前有关岩石在压模作用下破碎机理的观点有多种,但都很难解析压模所产生破碎坑的角度及大小问题,而且有关破碎坑大小试验资料也不一致:目前被较普遍接受的破碎坑的直径为,脆性岩石破碎坑的直径为压模直径的5~8倍,塑性岩石破碎坑的直径为压模直径的3~4倍。而根据前苏联A.T包尔德诺娃和H.H巴符洛娃的试验结论,脆性和小塑性岩石破碎坑的直径为压模直径的3~4倍,塑性岩石破碎坑的直径则为压模直径的5~8倍。两者之间相矛盾。因此有必要对岩石在压模作用下的破碎机理进一步探讨。
1 压模下岩石破碎机理的推理
有关岩石在压模作用下破碎机理,个人认为应遵循库伦—莫尔原则:接触面下方的裂纹并非是产生于最大剪应力,而是当接触面下方某处的应力沿剪切滑移面方向的分力大于摩擦力和内聚力之和时产生。压模下面某处的应力除了垂直方向的主应力σz外,还有水平径向方向的应力σr等应力。设τ为沿剪切滑移面方向的应力、σ为剪切滑移面上的正应力,那么压模下面某处沿剪切滑移面方向的应力τ及剪切滑移面上的正应力σ分别为:
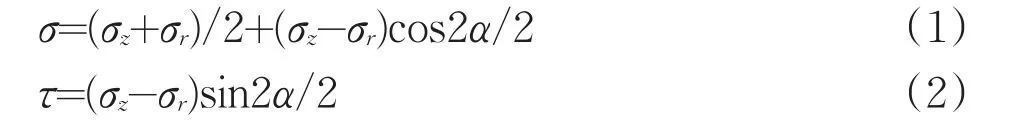
式中:α——最大主应力与剪裂面法线之间的夹角。
根据库伦—莫尔原则,当沿剪切滑移面方向的应力τ满足下面条件时产生剪切裂纹。

式中:σ——剪切滑移面上的正应力;
ψ——摩擦角;
C——内聚力。
压模下面某处垂直方向的主应力σz及水平径向方向的应力σr可通过下面公式求得:
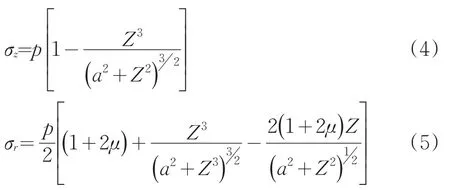
将τ=σtanψ+C对Z求导并使其等于零,便可得到剪应力τ减去摩擦力(σtanψ)后为最大值的深度Z0:
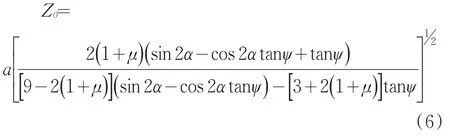
式中深度Z0是产生剪切裂纹的源点,a为压模半径,最大主应力与剪裂面法线之间的夹角α=π/4+ψ/2。压头下面岩石破碎的方式推理如下:如图1所示,岩石在负载作用下首先产生接触变形,然后在接触面下方Z0处产生剪切裂纹源1;在接触面边缘则产生最大拉应力,形成赫兹裂纹2,然后裂纹源扩展和交汇,沿裂纹交汇线形成脱离围岩的锥状独立岩体,此时独立岩体内部及下面的围岩已存在内伤(裂纹),极易在压力下剪切破碎。当独立岩体在压力下向下挤压时,该独立岩体与下面围岩的重叠部分首先被挤压破碎并被压密成密实体,在独立岩体及其下面的岩石在压头的压力下剪切破碎的同时,密实体通过传递的压力使其下面的岩石沿剪切方向压缩并因此对围岩产生挤压,当压力增加到一定程度时,水平方向的挤压力将围岩(与水平面)沿剪切角方向挤压崩离,形成锥体破碎坑。
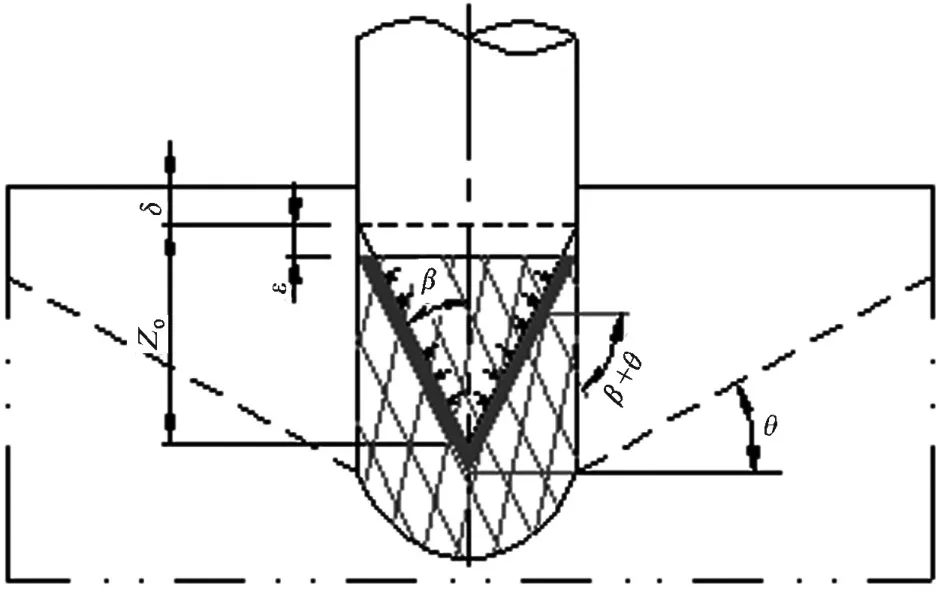
图1 岩石在压力作用下产生剪切破碎坑示意图
2 破碎坑大小及压入硬度的推算验证
2.1 破碎坑大小的推算
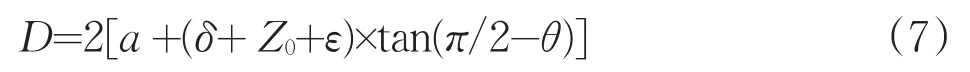
破碎坑的大小可按上述推论进行推算,其直径为:式中θ为岩石的剪切角(θ=π/4-ψ/2),δ为在压头压力作用下产生剪切裂纹源点前的压缩深度,ε为独立岩体的压深,根据岩石的变形性质,脆性岩石主要为坚硬致密以及坚硬岩石,参考工程岩体分级标准附录C表C.0.1、常见岩石的强度及泊松比可知,其摩擦角ψ通常大于50°,泊松比μ通常小于0.25。根据(6)式和(7)式可得:在不考虑δ及ε的情况下,破碎坑的直径D=9.2~15.7a,从而可得出脆性岩石破碎坑的直径与压模直径之比为4.6~7.85倍,若考虑δ及ε,则破碎坑的直径为压模直径的5~8倍;至于塑性岩石(摩擦角ψ<50°,泊松比μ=0.2~0.35),通过计算,在不考虑δ及ε的情况下,其破碎坑的直径为压模直径的3~5倍,受δ及ε的影响,破碎坑的直径应为压模直径的4~6倍,个别岩石(如片理平行于压力方向的片岩)破碎坑的直径大于压模直径的7~8倍。计算结果符合试验结论。
2.2 压入硬度的推算
根据上述推论,使围岩产生剪切破碎坑的挤压力F挤来自密实体传递的压力,这些压力将破碎岩石沿剪切角方向推动,在克服摩擦力后将剩余压力作用在围岩上,最终导致剩余压力的水平分力将围岩挤压崩离,形成锥体破碎坑。
假设锥状独立岩体的锥顶角为2β(为便于计算,将其当成圆锥体。β=arctana/Z0),来自压模的压力为Fσ,那么密实体传递的压力为Fσ/sinβ,该作用力沿剪切面的分力为Fσ×cosθ/sinβ,所克服的摩擦力为Fσ×sinθ× tanψ/sinβ,故其沿剪切面方向的剩余压力为:
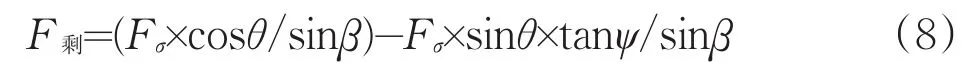
由于剪切面方向与水平面方向的角度为β+θ,因而使围岩产生剪切破碎坑的水平挤压力等于F剩×cos(β+ θ),即:
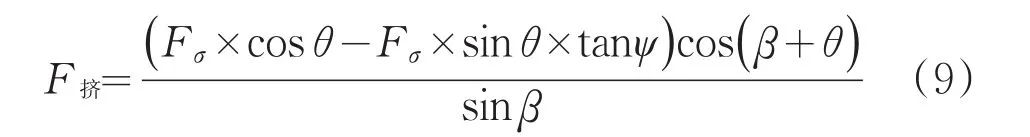
破碎岩石所需要的作用力通常按抗压强度×受压面积计算,即:

式中:σC——岩石的抗压强度;
MC——受压面积。
假设Mτ为剪切面积。则MC=Mτ×sinθ(θ为剪切角),上式可换算为:

岩石剪切破碎坑的侧面积(剪切面积)为:
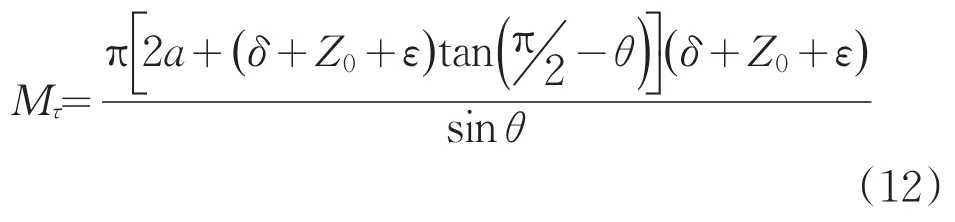
由(11)式和(12)式可得,使岩石产生剪切破碎坑的挤压力F挤为:
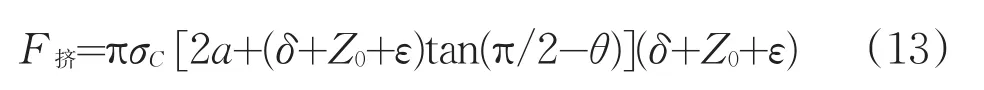
对于压头的压人深度(δ+ε),为便于计算,脆性岩石可当成弹性体来计算。即:

式中:E——岩石的弹性模量。
塑性岩石的压人深度(δ+ε)可按破碎坑深度与其比值为2.5~5计算:

岩石的压入硬度可通过(9)式、(13)式、(13)或(14)以及σ压=Fσ/πa2进行推算,例如某石英岩的单轴抗压强度σC=350MPa;ψ=60°;E=7×104MPa所对应的μ=0.12,可推算出其σ压=783 MPa。
3 影响压入硬度的因素及可钻性等级的划分
通过计算可知,影响岩石压入硬度的主要因素不仅有抗压强度σC,还包括摩擦角ψ以及泊松比μ:σC越大,则压入硬度越大;μ主要影响破碎坑的深度以及作用于围岩的水平挤压力(μ越大,则Z0越大,破碎坑越深;而β则越小,水平挤压力F挤越大);ψ不仅影响破碎坑的深度以及作用于围岩的水平挤压力,还影响破碎坑的顶角(ψ越大,破碎坑越深、越大,作用于围岩的水平挤压力F挤越大)。在抗压强度相同的情况下,致密岩石、摩擦角较小的岩石由于产生的破碎坑小(剪切面积小),所测得的致密岩石的压入硬度会偏小,但由于作用于围岩的水平挤压力F挤小,其实际上的压入硬度(在破碎坑大小相同的情况下)反而更大。
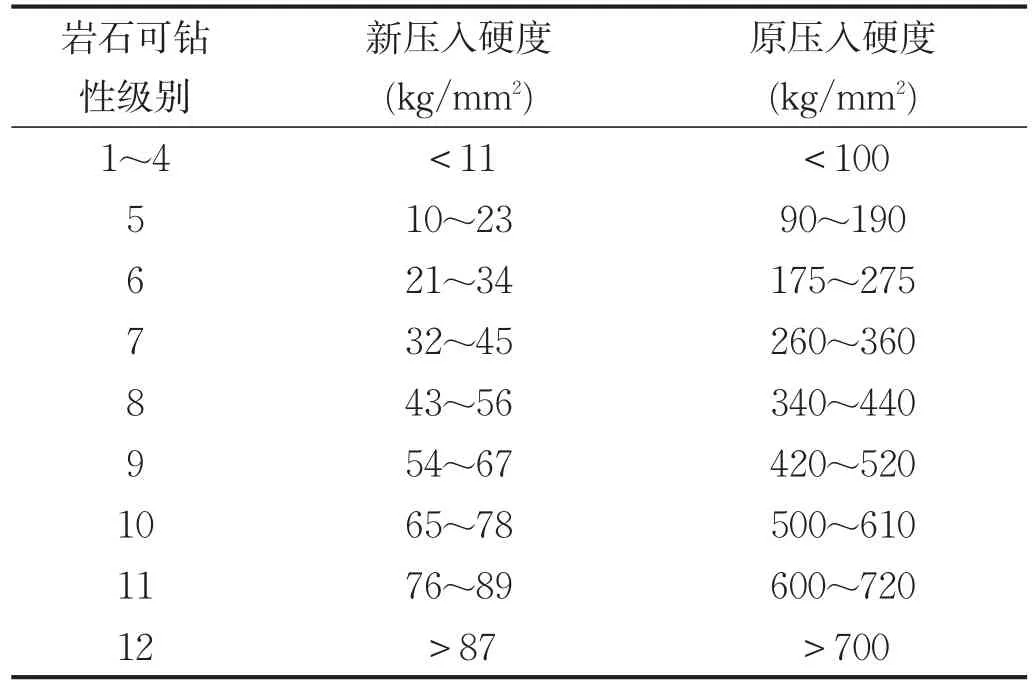
表1 岩石可钻性分级表
由于压头压入不同岩石产生的破碎坑的深度及大小不同,因而光用压入硬度来表示岩石的可钻性级别会不大准确。个人认为压入硬度应考虑破碎坑深度及大小的因素,用压入硬度除于破碎坑深度及半径与压头半径之比的乘积来表示,这样所得的压入硬度新值更能反映岩石的可钻性,压入硬度=700kg/mm2的岩石(可钻性12级)主要为坚硬、致密的岩石,其摩擦角ψ通常大于55°,泊松比μ通常小于0.12,弹性模量E通常大于7×104MPa。当ψ=55°,μ=0.12,E=7×104MPa时,求得破碎坑深度与压头半径之比=1.439,破碎坑半径与压头半径之比=5.564,故其压入硬度新值=87.4kg/mm2;同样,可求得压入硬度=90kg/mm2的岩石(摩擦角ψ通常小于35°,泊松比μ通常大于0.35,破碎坑深度与压人深度的比值为2.5)的压入硬度新值为9.5kg/mm2,因而建议岩石可钻性按表1进行分级。该分级可比较合理地反映岩石的可钻性,例如某寒武纪石英砂岩的抗压强度σC为68 MPa,摩擦系数为0.54(摩擦角ψ为28°),弹性模量E为5.4×104MPa,所对应的泊松比μ为0.14。通过推算,按原可钻性分级推算出的压入硬度为159kg/mm2,可钻性5级;而测试的可钻性同为5级中粒石英砂岩(122kg/mm2)钻进的实际时效为0.58m/h,按钻进时效分则为11级,差别很大;而若按表1分级进行推算,其压入硬度新值为66kg/mm2,可钻性9~10级,与钻进时效比较接近。
[1]修宪民,等.岩石力学性质及可钻性分级研究[J].云南地质,2001(3).
[2]武汉地质学院.钻探工艺学(上册)[M].地质出版社,1980.
[3]屠厚泽,高森.岩石破碎学[M].地质出版社,1990.
[4]张祖培,刘宝昌.碎岩工程学[M].地质出版社,2004.
[5]中华人民共和国水利部.GB50218-94工程岩体分级标准[S].
[6]顾晓鲁,等.地基与基础[M].中国建筑工业出版社,1993.
P634.1
A
1004-5716(2015)01-0070-03
2014-05-27
2014-12-08
吴其干(1965-),男(汉族),广东梅州人,工程师,现从事探矿工程技术和相关管理工作。

