基于有限元强度折减法的边坡安全系数的敏感性分析

张 旭，罗浩然，余 凯

(1.西南石油大学资源与环境学院，四川成都610500；2.中国地质科学院地质力学研究所，北京100081；3.中国地质大学<北京>工程技术学院，北京100083)

基于有限元强度折减法的边坡安全系数的敏感性分析

张 旭*1，罗浩然1，余 凯2,3

(1.西南石油大学资源与环境学院，四川成都610500；2.中国地质科学院地质力学研究所，北京100081；3.中国地质大学<北京>工程技术学院，北京100083)

随着边坡稳定性被广泛研究，对于边坡安全系数的敏感性分析具有重要意义。以均质边坡为例，探讨了岩土体抗剪强度参数以及屈服准则的选取对边坡安全系数的影响。通过边坡稳定性安全系数影响因素的敏感性分析，计算结果表明：①随着坡角的减缓，边坡安全系数逐步增大。②泊松比对安全系数影响不大，计算时可根据经验选取。③抗剪强度参数与安全系数呈正相关，并且具有一定线性关系。④不同的屈服准则得到的安全系数不同：不同屈服准则计算出的安全系数具有相对稳定性，也就是说随着内聚力的变化，不同屈服准则得到的安全系数的变化保持相对稳定。最后总结探讨了强度折减法获取边坡稳定性安全系数存在的问题，并针对这些问题，提出了作者的看法。

边坡；D-P准则；安全系数；内聚力c；内摩擦角φ

岩石、混凝土和土壤等材料都属于颗粒状材料，受压屈服强度远大于受拉屈服强度，且材料受剪时会发生剪胀效应，常用的Von-mises屈服准则不适用于这类材料。在土力学中，常用的屈服准则有Mohr-Coulomb准则被大多商用软件FLAC3D、ADINA采用。在边坡稳定性分析中常用的方法是极限平衡法，有如下缺点：①将土体看做刚性体，忽视边坡岩土体本身的弹塑性变形；②边坡破坏过程内部应力分布和变形不断调整；③假定滑面，滑面上应力分布的简化；④不适用于非均质材料；⑤只考虑强度特性，不能考虑实际的应力应变关系。

经典极限分析法（极限平衡法、滑移线场法、上下限分析法与变分法）适用于工程设计，但是适应性差。相比于有限元法适应性广但无法自动算安全系数，有限元法既适用于工程设计且适用性广。

对于岩石等材料用Drucker-Prager屈服准则更能准确描述这类材料，可得到较为精确地结果。20世纪70年代英国科学家Zienkiewicz就已经提出采用增加外荷载或降低岩土体强度的方法来计算安全系数[1]。随着计算机技术与计算力学的发展，岩土工程极限分析有限元法有着良好的发展前景[2]。

1 有限元强度折减法

强度折减法的核心理论是通过不断降低岩土体c、φ值，直到破坏（公式1、2）。

有限元方法边坡失稳判据主要有：

（1）滑面塑性区贯通，表明滑移面上每点都达到极限平衡状态[3]；

（2）滑动面上的位移与应变产生突变，产生很大且无限制的塑性流动；

（3）有限元计算不收敛，采用力或位移不收敛作为边坡破坏判据。

郑颖人认为土体滑动面塑性区贯通是土体破坏的必要条件[2]，但不是充分条件。本论文选择计算不收敛或者等效塑性区贯通作为土体破坏的判据[4]。

2 D-P准则

Drucker-Prager屈服准则是对Mohr-Coulomb准则的近似，用以修正Von-mises屈服准则（在Vonmises表达式中包含一个附加项）。其流动准则既可以用相关流动准则，也可以用不相关流动准则。不考虑材料硬化，因此其屈服面并不随着材料的逐渐屈服而改变。然而其屈服强度随着侧限压力（静水压力）的增加而增加，其塑性行为被假定为理想弹塑性。另外，此种材料考虑了由于屈服引起的体积膨胀，但不考虑温度变化的影响。

D-P准则考虑平均应力p或I1，将Mises强度准则推广为：即广义Mises条件[5]。

3 ANSYS内置的D-P准则推导

Mohr-Coulomb破坏准则公式表达为：

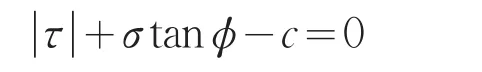
式中：τ——剪应力；

c——内聚力；

φ——内摩擦角。

当用摩尔圆表示时，准则可以写为：

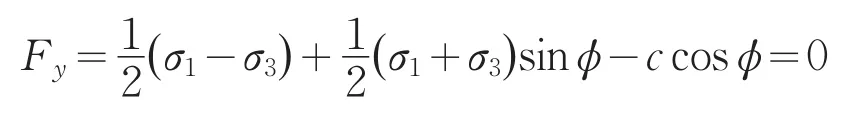
Mohr-Coulomb准则的屈服面在主应力空间中表示为六面体锥形。对屈服方程求导将产生奇点（不连续点）给数值计算带来很大困难。

现引入应力第一不变量I1和偏应力第二不变量J2以及Lode角，将主应力按照σ3≤σ2≤σ1排序，屈服准则又可以改写为：

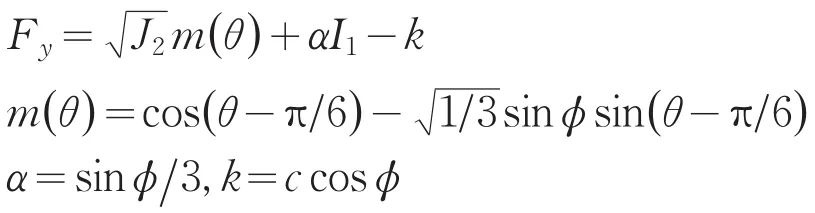
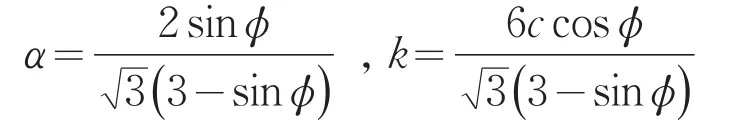
同理可得D-P准则外接M-C准则内角点、内切M-C准则、与M-C准则等面积等情况下α、k的值（表1）。

表1 各准则参数换算表[5-8]

塑性势函数与膨胀角φf有关，当φf=φ，流动规则为关联流动规则，即塑性势面和屈服面重合。塑性应变垂直于屈服面并且发生体胀；当φf＜φ时，体胀减小，当φf=0不发生体胀，并且流动规则变为非关联流动。

4 计算结果及结论

按照国标工程岩体分级标准规定的物理力学参数：确定5种岩体基本质量等级的物理力学参数见表2。

以Ⅴ类岩体物理力学参数建立地质模型，基于ANSYS的强度折减法计算边坡的安全系数F。模型尺寸见图1。

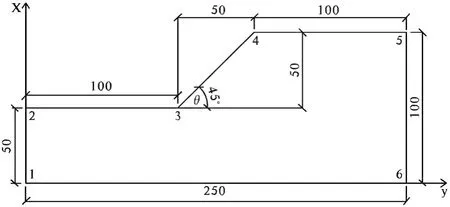
图1 模型尺寸图

有限元建立模型：PLANE82弹塑性单元，模型的力学参数首先选定为重力密度γ=20kN/m3，坡角θ=40°，内摩擦角φ=19.6°，粘聚力c=42kPa，变形模量E=1GPa，泊松比ν=0.25。边界条件为左右两侧水平约束，下部水平竖向约束，采用非关联流动。自由四边形网格划分。

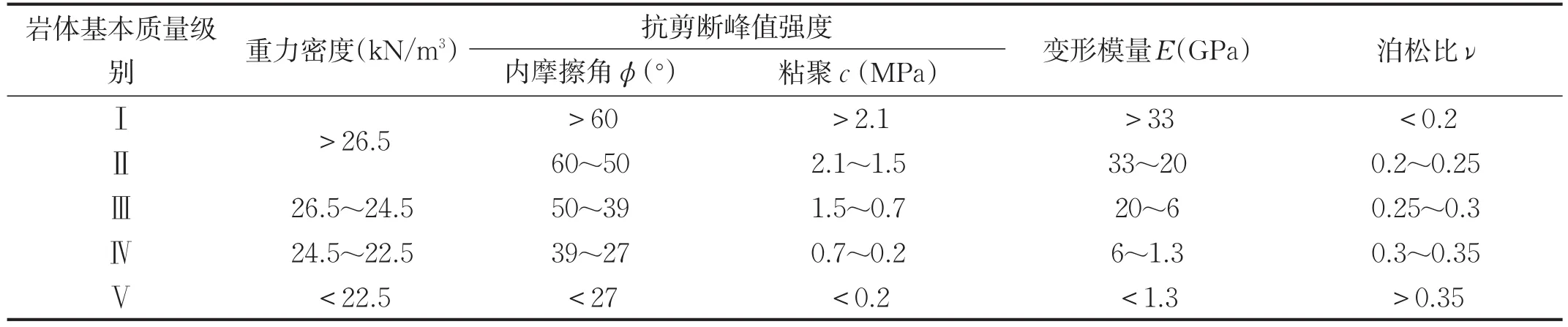
表2 岩体物理力学参数

4.1 泊松比对安全系数的影响

保持其他参数不变，改变泊松比的值。计算结果见表3。

表3 泊松比的变化对安全系数的影响

计算表明泊松比的取值对安全系数计算结果的影响不明显，但是对塑性区的分布有很大影响，泊松比越小，塑性区分布范围越大。所以泊松比参数在计算边坡安全系数时，在没有试验数据的情况下可以根据经验取值。

4.2 坡角对安全系数的影响

由于边坡的坡角随着时间的变化，不断发生改变，改变坡角分析边坡稳定性安全系数变化具有重要意义。计算结果（图2）表明：①随着坡角的变缓，潜在滑面趋于圆弧形；②缓坡角更易发育多级旋转滑坡；③坡角大于60°的边坡不稳定，但是近垂直边坡稳定性具有一定的稳定性；④在人为因素、降雨等诱发条件下，40°左右的边坡可能会失稳，一般达到天然休止角会变得相对稳定。

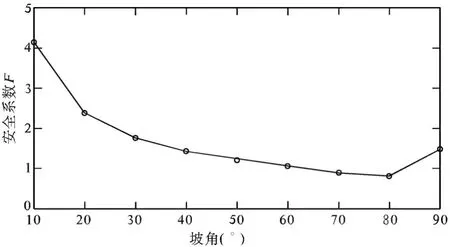
图2 坡角变化对安全系数的影响

4.3 c、φ值对安全系数的影响

在不考虑地下水因素前提下，抗剪强度参数（内聚力、内摩擦角）对边坡稳定性有着重要影响。计算结果（图3）表明：①c,φ变化对边坡稳定性有一定影响；②φ保持不变，c每增加5kPa，安全系数增加0.04～0.08；③c保持不变，φ每增加2.5°安全系数增加0.09～0.11。

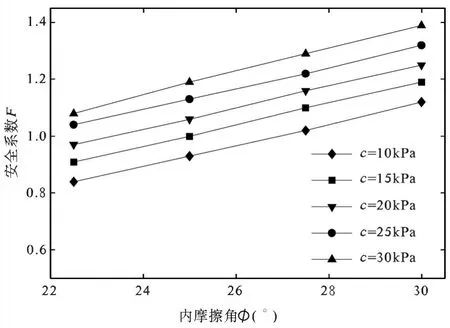
图3 c,φ值对安全系数的影响

4.4 流动法则对安全系数影响

ANSYS程序内当膨胀角等于内摩擦角，即φf=φ，流动规则为关联流动规则，即塑性势面和屈服面重合。塑性应变垂直于屈服面并且发生体胀；当φf＜φ时，体胀减小，当φf=0不发生体胀，并且流动规则变为非关联流动。

计算结果表明（表4）：同一简化准则在关联流动法则下的计算结果比非关联流动法则偏大0.08～0.10。

4.5 准则选取对安全系数的影响

D-P系列准则能否正确使用取决于岩土体不同的应力状态。研究表明，采用DP1准则与传统的摩尔—库仑屈服准则的计算结果有较大误差，偏于不安全。徐干成和郑颖人在1990年提出的摩尔—库仑等面积圆D-P准则[6]（DP4），计算表明它与摩尔—库仑准则十分接近，使有限元数值计算变得方便。但是非关联流动规则不能保证解的唯一性以及弹塑性系数矩阵一般也不对称[9]，当然也有其优越性，能使屈服函数符合实际又能保证塑性应变计算中不出现奇异性[3]。

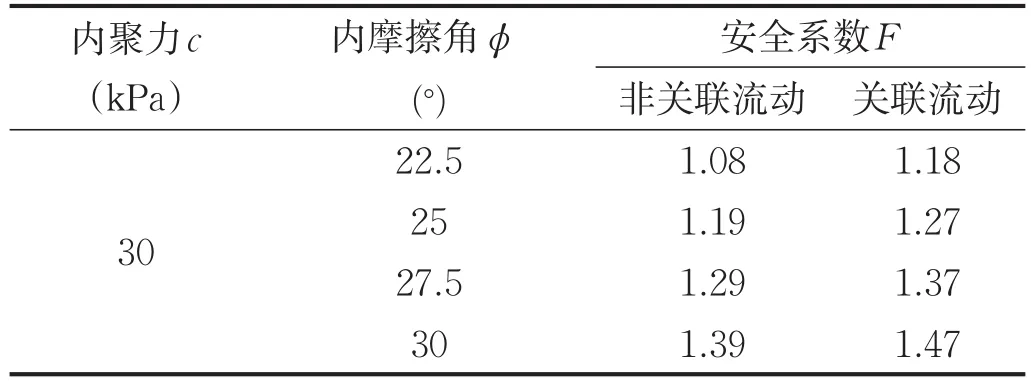
表4 流动法则对安全系数的影响

重力密度γ=20kN/m3，坡角θ=45°，内摩擦角φ=22.5°，变形模量E=1GPa，泊松比ν=0.25不变的情况下，来讨论不同屈服准则内聚力变化对安全系数产生的影响。按照表1换算各参数见表5，计算结果见表6、图4。

表5 各准则参数换算关系

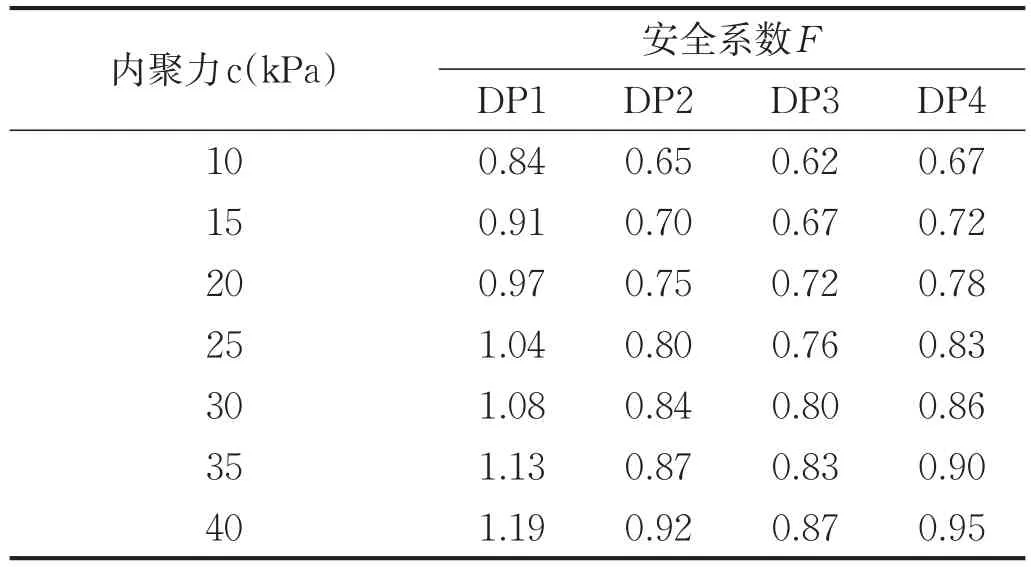
表6 ANSYS不同DP准则求得的安全系数对比

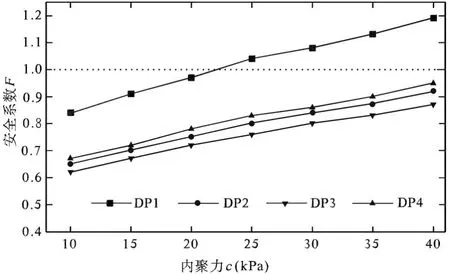
图4 准则选取对安全系数的影响

通过计算可以发现，有如下规律：①安全系数随着内聚力的增加不断增大，具有一定线性关系[10]；②不同屈服准则计算出的安全系数具有相对稳定性，也就是说随着内聚力的变化，不同屈服准则得到的安全系数的变化保持相对稳定；③DP准则匹配MC准则来计算边坡稳定性安全系数的时候，DP准则外接MC外角点（DP1）时为边坡稳定性安全系数的上限，DP准则内切MC准则屈服面内角点（DP3）时为边坡稳定性安全系数的下限[11]；④当使用ANSYS内置程序计算得到的安全系数用于工程设计偏于经济或危险，使用DP3计算结果偏于保守或安全（图5）。

图5 各准则安全系数比较

5 探讨

本文以均质边坡为例，探讨了岩土体抗剪强度参数以及屈服准则的选取对边坡安全系数的影响。利用强度折减法获取边坡稳定性安全系数仍存在几方面问题。

（1）当使用ANSYS内置程序计算得到的安全系数用于工程设计偏于经济或危险，使用DP3计算结果偏于保守或安全，如何使得计算结果技术可行经济合理值得深入研究。

（2）强度折减法一般适用于均质边坡，对于非均质边坡“单层强度折减还是每层均强度折减？或许这种方法就不适用于非均质边坡？”这些问题还有待进一步研究。

（3）强度折减法因其计算方便，直接能够得到边坡稳定性安全系数，被广泛应用到工程实际中，然而其强度折减后的物理意义“失真”，不同学者持着不同的态度。

（4）对于同一边坡不同的计算人员得到的安全系数可能不同，影响因素有多种，如何实现行业的规范化数值模拟和边坡治理的工程设计，将是长期的研究目标。

[1]Zienkiewicz O C,Humpheson C and Lew is R W.Associated and Non-Associated Visco-Plasticity and Plasticity in Soil Mechanics[J].Geotechnique,1975,25(4):671-689.

[2]郑颖人,赵尚毅,孔位学,邓楚键.极限分析有限元法讲座—Ⅰ岩土工程极限分析有限元法[J].岩土力学,2005,26(1)：163-

[3]栾茂田,武亚军,年延凯.强度折减法有限元中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3)：1-8.

[4]赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座—Ⅱ有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26 (2)：332-336.

[5]郑颖人,陈长安.理想弹塑性岩土的屈服条件与本构关系[J].岩土工程学报,1984,6（5）：13-22.

[6]徐干成,郑颖人.岩石工程中屈服准则应用的研究[J].岩土工程学报,1990,12（2）：93-99.

[7]邓楚键,何国杰,郑颖人.基于M-C准则的D-P系列准则在岩土工程中的应用研究[J].岩土工程学报,2006,28（6）：735-739.

[8]郑颖人,赵尚毅.岩土工程极限分析有限元法及其应用[J].土木工程学报,2005,38(1)：91-104.

[9]李广信.高等土力学[M].清华大学出版社,2004.

[10]赵尚毅,郑颖人,时卫民,王敬林.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3)：343-346.

[11]赵尚毅,郑颖人.用强度折减法进行节理岩质边坡稳定性分析[J].岩石力学与工程学报,2003,22(2)：254-260.

TU47

A

1004-5716(2015)01-0011-05

2014-02-13

2014-02-13

张旭（1989-），男（汉族），河北任丘人，西南石油大学地质工程专业在读硕士研究生，研究方向：地质构造与地质灾害评估。