数里有“我”:激扬儿童灵性的必由之路
——以苏教版三年级上册“认识分数”为例
江苏南京市长江路小学(210000) 丁爱平
数里有“我”:激扬儿童灵性的必由之路
——以苏教版三年级上册“认识分数”为例
江苏南京市长江路小学(210000) 丁爱平
长期以来,见数不见人的数学课程观压制着儿童的天性,泯灭着儿童的灵性。“认识分数”一课,有数,更有“我”。数里有“我”,旨在尊重儿童发展的原生态过程,尊重儿童生长的需要和动机,最大限度地促进儿童灵性的发展。
原生态 我的数学 儿童灵性
一、梳理“我”准备
师:关于“分数”,你已经知道了什么?
生1:我知道一个蛋糕分成两份,一份是二分之一。
师:分?随便分成两份?
生1:两份要一样多,要平均。
师:平均这个词说得好!
生2:我还知道二分之一的横线是分数线,1是分子,2是分母。
师:大家都知道了二分之一,谁能把它写出来?关于分数,你最感兴趣的问题是什么?
生3:以前写加法、减法、乘法、除法、竖式都是从上往下写的,分数怎么从下往上写啊?
师:谁知道为什么?(全班沉默)关于分数的读写顺序,就像汉字的笔顺一样是一种规定。
生4:长方形纸能折出三分之一吗?
生5:能!把长方形这样竖着(用手比划),能折出三分之一。
生6:不能吧?
师:问得好!待会咱们动手试试。
生7:是不是所有的图形都有二分之一?
生8(肯定地):是的!
生9:不规则的图形怎么折呀?
师:有意思!先保留着这个问题,学完了这节课看看你们能不能解答。
生10:二分之一为什么比四分之一大?
生11:四分之一是不是二分之一的一半?
师:大家提的问题太有价值了!太善于思考了!让我们带着问题走进——分数。
二、“我”尝试
1.学习二分之一
师:这样分,其中的每一份是这个蛋糕的二分之一吗?(课件出示不平均分)
生1:不是!要从中间分。(课件出示)
生2:两份要一样多。
生3:要平均。
师(举起蛋糕模型卡片):谁来平均分?(学生对折,教师剪开模型,学生上讲台演示并叙述“把一块蛋糕平均分成2份,其中的每一份都是它的二分之一”。)
师:大家通过预习都知道了2是分母,1是分子。谁能解释分母2表示什么意思?分子1表示什么意思?
生4:2表示平均分成了2份,1是表示其中的1份。
师:在这句话中,你觉得哪些词特别重要?(生答“平均分、每份、它”)“它”指的是谁?
生5:这个蛋糕。
师(拿出一个小小的蛋糕模型):黑板上的半块是它的二分之一吗?
生6:不是!你手里的这个蛋糕太小了。
师:是吗?它的二分之一有多大?折折看。(学生对折)对于分数,一定要说明白这一份是谁的几分之一。
2.折出长方形的二分之一
师:这张长方形纸,你能折一折,把它的二分之一涂上颜色吗?(学生展示作品)为什么涂色部分形状不同,但都可以用二分之一表示?
生7:每个人的两份都一样大。
生8:因为都是平均分成2份,涂了1份。
生9:还可以这样斜着折!(平均分成两个梯形)
师:是不是随便怎么斜着折都可以啊?这样斜着折(折出不相等的两个梯形),行吗?看来斜着折出它的二分之一还有窍门呢!这个奥秘我们以后会研究到。
三、“我”探究
1.认识几分之一
师:除了二分之一,你还想探究几分之一?怎么来探究呢?老师有一个建议。第一步,想一想,创造的这个分数表示把一张纸平均分成几份啊?取其中的几份?第二步,折一折,提醒自己“是平均分的吗?”数一数“总份数符合要求吗?”第三步,涂一涂,把其中的几份涂上阴影?第四步,说一说是怎样创造这个分数的,同学之间互相介绍。请大家用手中的纸片来创造出你喜欢的分数。如果你发现自己的作品与众不同,请到讲台上展示。
师:有创造出三分之一的吗?想一想,可以创造出长方形纸的三分之一吗?
生1:可以。折的时候看准了。
生2:用尺量,得出的数再除以3。
师:真会动脑筋!全班47个图形中,尽管形状不同、大小不同,但都创造出了很多分数。现在,谁能解释问题“是不是所有的图形都有它的二分之一?”
生3(肯定地):是!
生4:只要平均分成2份,取其中的1份。
生5:不规则的图形也有它的二分之一?
生6:有,就是一半。
生7:那怎么折呀?
师:折起来很困难,但是在数学上确实是存在的。谁知道分数线是谁发明的?(学生摇头)赶快找,书上有。
2.比较分数的大小
师:今天有两只小猪过生日,如果兄弟俩平均分这个蛋糕,每人分到多少?怎么能忘了亲爱的爸爸妈妈呢?如果四个人平均分,每人可以分到多少?观察二分之一和四分之一,你发现了什么?小猪的6个好朋友也来庆祝生日了,10个人平均分呢?假如有100个人来平均分(课件出示),每只小猪分到的蛋糕太少了,为什么大家还在笑呢?
生8:小猪过生日,大家一起分享蛋糕,很开心!
师:这就是分享的快乐!
四、“我”检测
1.书上想想做做1、2。
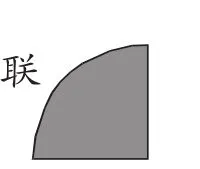
2.想象力达人秀:看到右图的涂色部分,你联想到哪个分数?
3.习题:小伙伴们吃完蛋糕,出去散步。从这里开始走,起点可以用什么数表示?小猫一下就溜到了终点。它跑了完整的一条路,可以用1来表示,小猪呢?(课件出示:小猪才跑了这条路的二分之一)小猪跑到哪里了?
师:小青蛙跑了这条路的四分之一。它跑到哪里了?(学生指)为什么在这里?
生1:把二分之一再平均分,一共分成4份。
师:四分之一是不是二分之一的一半?这个问题问得真好,谁能回答?
生2:是二分之一的一半,把二分之一再平均分成2份,就是四分之一了。
师:奇迹发生了(显示这条路变长了),小猪走过的还是现在这条路的二分之一吗?(学生答“应该是三分之一”。教师演示三等份)青蛙呢?(学生用手比划后发现是六分之一。课件演示把长方形路面演变成一条线段)
生3:我发现今天认识的几分之一的分数都在0和1之间。
生4:为什么这些分数的分子都比分母小?生5:都是取1份的呀!
师:太聪明了!又有新的问题了!
生7:那有没有分子比分母大的分数?
生8:有!我看到过二分之四。
生9:有没有分子分母相等的分数?(有学生说四分之四)
生10:有没有最大的分数?
师(板书一个大大的问号):我们将带着新的问题继续探索分数的奥秘!今天大家回家后把自己最得意的收获变成问题,考考爸爸妈妈,听听他们的想法;每人准备一两道小题目,明天带来考考同学,比比谁有水平。
【我的思考】
“认识分数”这一课的经典版本太多了,而我这节课所要表达的是一个字——“我”。“我”的含义有两层:一是学生的自我能动,课堂是属于学生的,要努力实现学生个体的主动建构;二是教师的自我能动,教师之“我”已经与数学相融,“我”的学科精神与气质将激励、引领、成全每一个儿童。教师听完本课后说得最多的是:“太好了,孩子太有灵性了,那些问题、那些想法连我们都没有想到。”
在“我准备”这一环节,我通过课前预习让学生提出自己感兴趣的问题。这样做有三个目的:1.激发学生自主思考;2.创设广阔的思维空间;3.便于找准最佳教学起点。在传统教学中,或是教师直接设问,或是创设情境,或是复习铺垫,无论哪种方式其实都是教师“自作多情”地认为这些做法是学生迫切想知道的。而通过本课的教学,我却发现以前教师所认为重要的问题学生并不感兴趣,学生关心的是“分数怎么会倒着读、倒着写呢”等这些孩子气的问题,他们迫切希望能从教师那里讨一个说法,于是就产生了强烈的需求,这样的课堂自然能够生发动人的灵性。
在“我探究”这一环节,教师首先要对“我准备”环节中的问题进行过滤和分类。简单的问题边问边解决,复杂的问题留着过后解决;重要的问题重点解决,非重点的问题可以个别交流。这一环节,是最考验教师教学功力的。教师知识面要非常广,对教学内容要非常熟悉,反应还要特别快。课上有学生问分数是怎样产生时,就能马上让学生翻开书查找资料。
在“我检测”这一环节,充分尊重了儿童的认知特点,展开了趣味盎然的练习。想象力达人秀、小动物走路,这些形式多样的练习尊重儿童的认知特点、思维习惯和审美情趣,并且所有的形式都紧扣内容,有意思且有意义。上这节课,真可谓酣畅淋漓。某些时刻,我已经分不清到底是数学造就了儿童的闪亮灵性,还是儿童造就了数学的魅力无限,“我”与数学早已水乳交融!
一般意义上说,要完全实现“数里有我”,绽放儿童的灵性,需处理好以下几个关系。
第一,常态之“我”与公开之“我”的关系。随着各种新的教学模式纷至沓来,我们要把持住的是彻底的真实与纯粹。这节公开课的亮点不是套用什么新模式,而是学生童趣的、灵性的、真实的“我”思考。“数里有我”,这个“我”所追求的不是公开课舞台上的明星秀,而是和数学学科中的认数一样,静下心来一一计数,满十进一。公开之“我”就是常态之“我”。任何直奔“展示秀”而去的绚烂,不是我们追求的灵性,而是影响儿童数学学习品质的劣性。
第二,学生之“我”和教师之“我”的关系。把课堂的主动权让给了学生,学生自主提问、质疑争辩,很容易偏离教学的核心目标,此时是任其自由发挥,还是适可而止、聚焦核心?我认为,教师应瞄准恰当的时机介入,点拨、提醒、归纳,营造高质量的师生互动和生生互动。教师之“我”服务于学生之“我”,又不过于迁就宠溺,保持着温和的理性。只有在这种和谐共生的师生关系中,师生的生命灵性才得以尽情彰显。
第三,“我”和“我们”的关系。不可否认,本节课的画龙点睛之笔是由一部分有个性有思想的学生来推动完成的。教师要密切关注一群沉默的“小羊羔”,他们在倾听和观看中,是否有情智的触动?是否有积极的回应?一个班的学生,个性迥然,参差不齐。40分钟内,同桌互动、4人小组内互动、全班互动的频率、深度和广度都受到太多因素的牵制。如何关注每一个“我”,从而设计出匹配度高的教学,让“我们”各美其美、美人之美、美美与共?这还需要我们进一步深入研究。
(责编 金 铃)
G623.5
A
1007-9068(2015)35-014

