细节虽小,亦可成就课堂精彩
江苏连云港市黄海路小学(222000) 吴凌艳
细节虽小,亦可成就课堂精彩
江苏连云港市黄海路小学(222000) 吴凌艳
教学细节,指课堂教学过程中细小的环节或情节。教学细节能反映教师的教学水平,折射教师的教学理念,决定课堂教学的效率和质量。有效的课堂教学,要从细节的研究入手,在对细节的不断打磨中,使课堂教学效率得到有效提升。
教学细节 现场点击 策略探寻 数学教学 精彩 错误资源 课堂评价
教学细节,是指课堂教学中细小的环节或情节,是教学行为的具体分解,是构成教学行为的最小单位。可以说,教学细节是教师的一言一行、一颦一笑,是师生之间的心灵互动、行为组合,是在特定情境中学生对教学的瞬时反应……有位特级教师说过:“透过教学细节,可以看出教师的理念、境界、文化、智慧、魅力……”那么,在课堂教学中,教师应如何把握细节呢?
一、现场点击:课堂在无视细节中蹉跎
“千里之堤,溃于蚁穴。”杨再隋先生也说过:“忽视细节的教育实践是抽象的、粗浅的、迷茫的。”课堂会因为细节的疏忽,导致精彩与我们擦肩而过。
1.教学导入无的放矢,学生一头雾水
导入是课堂教学的重要环节,在一定程度上折射出教师的教学理念。课程改革后,许多课堂因为创设生动有趣的情境而变得有吸引力,但同时我们也要看到,有的教师为了创设情境而创设情境,不仅没有任何价值,反而让学生感到一头雾水,无所适从。
案例:苏教版六年级上册“倒数的认识”
师:生活中许多东西可以倒过来,如杂技演员可以倒立行走、茶杯可以倒放在桌上等,还有著名的句子“上海自来水来自上海”,从左往右或从右往左读都是一样的,数学里也有这样的知识。(师揭题并板书课题:“倒数的认识”)
师:什么是倒数?
生1:倒数就是将数倒过来或者倒着数。
生2:1的倒数是1,8的倒数是8,6的倒数是9。
……
这样的情境导入,没有把握概念的内涵,只是在“倒”字上下工夫,忽略了倒数的本质意义,不仅对学生的学习没有帮助,反而造成他们的认知偏差。
2.课堂提问无边无际,学生如云中漫步
提问是课堂教学的重要手段,是师生交流的主要途径。精彩的提问能诱发学生的思维,提高课堂教学效率。但在实际教学中,不少教师的提问过于简单,流于形式;也有的提问过难,超出知识范围,抑制了学生思维的积极性;还有的提问指向不明,使学生盲目回答,毫无价值。
案例:苏教版三年级下册“平均数”
师(多媒体出示游泳池,并说明游泳池的平均水深为1.40米):你们去游泳,安全吗?
生1:安全,可以在浅水区里游。
师:真的安全吗?
生2:安全,可以带救生圈,也可以叫家长陪同……
师(出示游泳池的剖面图,显示最深处为1.6米,最浅处为1.2米,中间处为1.4米):1.4米是怎样算出来的?你们知道它是什么意思吗?
……
诚然,教师问“你去游泳,安全吗”,目的是想让学生理解什么是平均数,但由于问题缺乏明显的数学指向,导致学生无法了解教师的提问意图,回答漫无目的,难以引发数学思考。
3.学习材料无所适从,学生眼花缭乱
数学课堂中,利用教、学具来帮助学生理解概念和公式也是教学常用的手段之一,可材料的选择是否具有简易性、典型性也直接影响着教学的有效性。
案例:苏教版二年级上册“四边形的认识”
教师准备了大量的四边形,如有缺角的长方形、凹的四边形和一些持征不是很明显的四边形等,让学生在众多的图形中找出四边形并概括出四边形的特征。由于图形太多,且特征不明显,学生看得眼花缭乱,花费了大量的时间来寻找四边形,最后对四边形特点的概括显得非常零碎。
学生对学习内容首次感知时,要抓住知识的本质特征,形成表象,在练习中进行变式、比较,认识才会深刻。上述教学中,材料过多、过杂,反而成了学生学习的绊脚石。
二、策略探寻:课堂在关注细节中提升
有效的教学,离不开对教学细节的关注。因此,教师要精心设计教学过程,在对细节的不断打磨中,使课堂教学效率得到有效提升。
1.精心预设流程,准确把握细节
教学细节的设计缘于对教材、学生和环境的理解与把握,缘于对各种教学资源的组合与利用。因此,教师要在教与学、师与生、生与生的交流互动中敏锐发现、及时捕捉、深入挖掘,寓教育于无痕。
案例:苏教版三年级下册“认识面积”
教师先引导学生温习旧知,再出示下面的方格图(如图1),图中有一个小黑点,要求学生将这个黑点向上平移2格,在学生操作示意后,教师在图中点出平移后的小红点。然后教师引导学生将这个小红点在刚才平移中行走的路线划出来,得到一条线段(如图2)。接着,让学生将这条线段向右平移4格,并思考这条线段会移到什么位置。事实上,这条线段的平移就像一把刷子在往右“刷”,即在方格图上“刷”出了一个占8个格子的长方形(如图3)。教师再引导学生在这个方格图上“刷”出两个大小不同的长方形,最后让学生观察比较自己的作品,明确有的面大,有的面小。在学生操作、感悟后,教师揭示面积的意义。
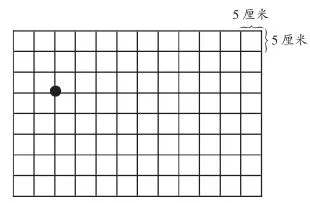
图1
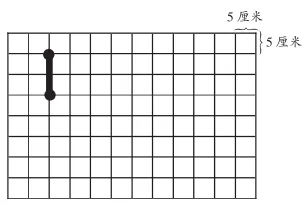
图2

图3
上述教学,教师紧紧抓住“移”这个动作细节来设计新课导入。尤其是“线动成面”的动作细节,通过形象直观的“点、线、面”的有序递进,使面积的引入自然流畅,于无痕处见教师的“匠心”。
2.把握课堂生成,成就细节精彩
叶澜教授说过:“课堂应是向未知方向挺进的旅程,随时都可能发现意外的通道和美丽的图景,而不是一切都必须遵循固定线路而没有激情的行程。”这就需要教师有一双发现的慧眼,善于捕捉,有意识地创造与开发,成就细节的别样精彩。
案例:苏教版一年级上册“认识立体图形”
课堂上,在学生把带来的各种物体(立体图形)分类后,有些学生把正方体、长方体放在桌子上,却紧紧地抓住几个球不敢放下。
师(观察了片刻后):生1,你为什么不把球放下?
生1:老师,球会跑的。
师(追问):它是怎么跑的?
生1:到处乱跑。(生1还自告奋勇地上台表演,证明给大家看)
师:在这些物体中,还有什么也会跑?
生2:圆柱,但它不会乱跑,而是比较听话地往前后或左右跑。
师:车轮是什么形状的?为什么不做成球体?
……
上述教学中,教师把握住学生“抓住球不敢放下”的细节,改变教学预设,巧妙引导,于惯常处开拓一片新天地,获得了别样的精彩。
3.利用错误资源,彰显细节魅力
数学活动是开放的,学生的思维如树枝般常会旁逸斜出,即使课前预设再充分,也不能完全避免错误。课堂教学中,如果教师敏锐地发现并充分关注学生的错误,耐心扣问,静静倾听,深入挖掘,才会了解学生的真实想法,实现课堂教学精彩生动的目的。
案例:苏教版四年级上册“用量角器画角”
学生先自主探究,初步形成画角的方法,接着尝试独立画角。教师在巡视中发现生1把一个105°的角画成了75度°,还有不少学生也出现这样的错误。于是,教师灵机一动,让生1上台板演。生1刚画完,就有学生开始嘀咕:“这个角是105°,怎么画成了锐角呢?”师故作糊涂,问道:“刚才生1画角时,你们在嘀咕什么?”“他画错了!”师:“那么,你们能说说为什么画错吗?”学生经过讨论,帮生1弄清了错误的原因:原来他画角时,在量角器上数刻度时数反了。师继续问学生:“他的错误,对你有帮助吗?”学生纷纷举手回答:“老师,画角时要看清刻度,可不能看反了!”“画角前,要先想一想是锐角还是钝角。”“老师,他的错误很特别,正确的角加上画错的角正好是平角。”师表扬这名学生,并马上追问:“假如生1又犯了同样的错误,画了50度的角,你能马上知道他要画的正确的角是多少度吗?”学生异口同声地回答:“130度。”这时,一名学生又有了新的想法:“老师,我还有一个新的想法,即画120度的角,只要先画60度的角就可以马上画出120度的角了。”多么精彩的发现呀,课堂响起了热烈的掌声。
上述教学中,面对学生的错误,教师没有草草处理,而是抓住这个契机,让学生自己寻找原因,激起学生对错误的争论,形成独到的见解。正是由于教师的随机应变,让错误精彩起来,成为课堂教学的一个亮点。
4.灵动课堂评价,升华细节精彩
如果说一堂成功的课是一曲动人的交响乐的话,那么,课堂评价则无疑是这首乐曲中跳动的音符。苏霍姆林斯基也说过:“教师无意间的一句话,可能造就一个天才,也可能毁灭一个天才。”作为教师,我们对学生的评价应该是深思熟虑的,使学生能在民主、愉快的气氛中思考与创新。
案例:苏教版四年级上册“交换律”
……
生1:我们小组验证减法也有交换律,如1-1=1-1、2-2=2-2、3-3=3-3……
师:好像说得有些道理哦!你们认为对吗?
生2:不对。那是在被减数和减数相等的情况下,如果被减数和减数不相等的话就不可以了,如2-3和3-2是不相等的,所以减法是没有交换律的。
师:太棒了!学会找一个反例去推翻假设,真是一个很好的思考方法,同时也是解决问题的重要手段。
……
对学生的评价,教师应尽量从正面引导,以鼓励、表扬为主,但如果一味地进行肯定评价,久而久之,会让学生无法分辨自己想法的合理性,带来不好的影响。所以,教师应对每位学生给予真诚的评价,这样才能使所有学生都能在课堂上倾吐心声,享受生命成长的喜悦。
总之,失败的细节给人以启迪,成功的细节给人以借鉴。著名导演张艺谋说过:“没有多少人能记住整部电影详细的过程,但却能记住某一闪亮的细节。”细节看似平常,但平常中蕴涵智慧;细节看似简单,但简单中孕育思想。因此,我们在课堂教学中要用心捕捉、关注细节,在细节中探索学生学习数学的有效途径,实现师生间的有效合作,在课堂的寻常处酝酿别样的精彩。
(责编 蓝 天)
G623.5
A
1007-9068(2015)35-035

