喷管分离流动模态转换过程壁压测量试验
王一白,陆星宇,李 波,刘 宇
(北京航空航天大学 宇航学院,北京 100191)
0 引言
对高性能火箭发动机的需求推动了高性能喷管的发展,而高性能喷管主要是通过提高喷管出口与喉部截面的面积比实现的[1]。大面积比的喷管在开机阶段会经历过膨胀,流动在喷管壁面上发生 分离 。 在 J-2S[2],SSME[3], LE-7A[4]以 及 Vulcain[5]等发动机的研发过程中都发现这种流动分离常常是非对称且不稳定的。这种非对称分离流动会导致巨大的非对称侧向力,往往对喷管本身和发动机造成损害。这种损伤已经成为大膨胀比发动机喷管设计的主要限制之一[6]。目前工程上解决该问题的主要策略是加强结构,代价是结构质量的增加。目前已经基本确定钟形喷管内常见的流动分离模态有两种:自由激波分离和受限激波分离。研究者们也提出了不同的分离准则和分离预测模型。但现有的所有模型都对具体喷管有依赖性,当喷管类型或型面参数发生较大变化时就难以获得满意的预测结果,反映了对该问题的理解仍然有待加深。
为了理解大膨胀比喷管过膨胀过程中不同流动分离模态及其转化过程的特征,对缩比推力最大抛物线 (Thrust Optimized Parabolic,TOP)喷管进行了壁面压强测量试验,并辅以数值对比计算,捕获到了两种典型的分离模态,获得了所用TOP喷管的分离模态转换压比范围。对于后续开展大面积比喷管的流动分离试验,掌握流动分离过程对应的工作压强比范围,提供了有益参考。
1 喷管设计与实验系统
试验所用喷管为最大推力抛物线喷管,其关键参数见表1。
喷管壁面0°与180°母线上对称布置了15个测压孔,受到加工条件限制,未采用孔轴线与壁面垂直的设计,而是使孔与喷管的轴线方向垂直,孔径2 mm,测压孔轴向间距均为6 mm。测压孔经由测压管接头再通过软管与压强传感器连接。

表1 TOP实验喷管关键参数Tab.1 Key parameters of the TOP nozzle used in experiments
压强传感器采用YZD扩散硅压强变送器(绝压),量程选择200 kPa,1 MPa和10 MPa,精度为±0.2%,不同传感器在各测点的排布见表2。
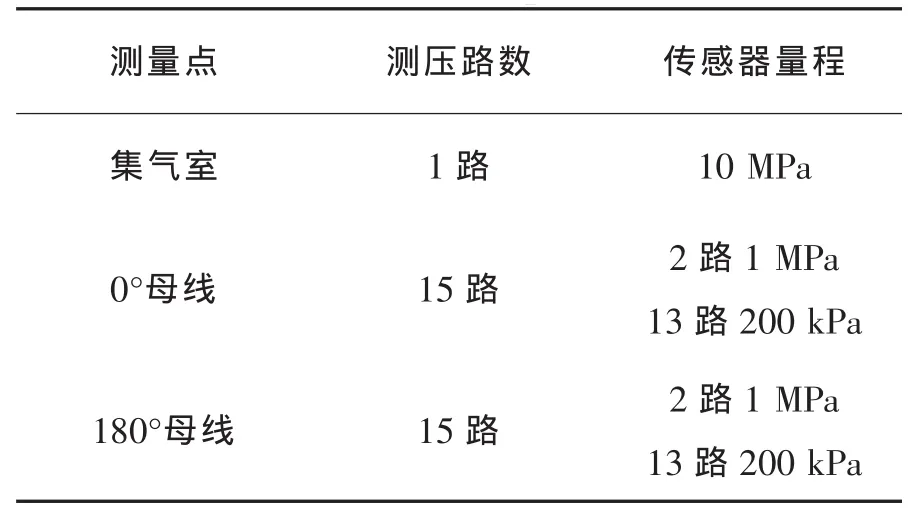
表2 压强传感器分布Tab.2 Distribution of pressure sensors
喷管扩张段传感器量程的选择是根据前期试验获得的压强范围选择的,试验发现喷管在集气室压强在3.5~4 MPa时喷管已经满流,而在室压低于3.5 MPa时壁面压强都在0.02~0.18 MPa之间,故大多采用了量程为200 kPa的传感器。压强高数值区域采用1 MPa量程。测量系统的数据采集卡采用PC-6325A光电隔离模入接口卡。
2 试验结果及数值仿真验证
2.1 流动分离下的喷管壁面压强分布
试验的测量目的在于获得不同压比下喷管壁面压强的稳态特征。为了得到较为稳定的试验数据,每次试验中发动机的工作时间不小于2 s,试验数据的采集时间均为5 s。根据后期数据处理的结果,发现每次稳定压强下工作的时间均超过了2 s,可以确保数据的有效性。

图1 喷管壁面0°母线压强分布Fig.1 Pressure distribution of 0°generatrix of the nozzle wall

图2 喷管壁面180°母线压强分布Fig.2 Pressure distribution at 180°generatrix of nozzle wall
图1和图2分别给出了不同试验压比下喷管壁面0°母线和180°母线的压强分布。图的右侧给出了试验测到的喷管压比(Nozzle Pressure Ratio,NPR),横坐标为以喉部为坐标原点及流动方向为正方向的位置坐标X除以喷管扩张段总长度L得到的单位化坐标。前期试验发现本试验中采用的TOP喷管流动分离的NPR上限在31附近,图中给出的NPR范围基本覆盖了流动分离的压比范围。
根据自由激波分离和受限激波分离的特点,可以认定试验中测到的壁面压强反映了这两种分离模态。
2.2 流动分离激波系的产生机理
在喷管中事实上存在两种扰动源,分别是喷管壁面和环境压强。从钟形喷管设计理念的角度可以解释喷管型面引起内激波系的机理。激波系一定是存在于超声速流场之中,因而对激波系影响最大的就是扩张段的型面。传统钟形喷管(包括理想喷管/IC、截短理想喷管/TIC、压缩截短理想喷管/CTIC、最大推力喷管/TOC、最大推力抛物线喷管/TOP)的扩张段设计都秉承了一次扩张一次整流的思想,即在喉部处采用小曲率半径的弧,使达到音速的气流快速膨胀,在最短的距离内实现加速,从而缩短喷管的整体长度。该阶段马赫数较低,剧烈型面变化带来的流动损失较小,因而缩短喷管付出的流动损失代价较小。这一阶段型面的切线斜率从喉部处为零单调增加到某一临界值,在此期间气流快速膨胀。该临界点后的型面切线斜率开始单调减小,直到喷管出口。这一段是为了使流动方向逐渐趋向于轴向,从而将工质的动量收拢到推力方向。
这种先膨胀后扭转流动方向的设计使得在切线斜率开始减小的地方容易产生曲线一阶或二阶不连续,相当于超声速气流遭遇拐角,这种型面会在流场中引发强扰动,因而形成激波。不同钟形喷管设计的差异在扩张段体现得最为明显,IC和TIC喷管在切线斜率的单调递减段采用了更为和缓的型面,使喷管内从轴线反射到壁面的膨胀波不再发生二次反射,从而使气流在喷管中实现无内激波的均匀流动(在满流情况下)。而除了IC和TIC喷管之外的所有钟形喷管都存在流动转折过于剧烈的问题,因而都存在壁面曲率导致的内部激波。
与壁面扰动并存的是压强扰动,即环境压强对流动的扰动。在流动严重过膨胀时,超声速的低压流动会遭遇高背压,从而形成激波。
2.3 壁面压强分布与流动分离模态的对应关系
2.3.1 自由激波分离
对于本试验所采用的TOP喷管,一般会随着NPR的增加而依次经历自由激波分离、受限激波分离和第二次自由激波分离。在自由激波分离模态下,从喉部喷出的流动会首先贴壁流动,在下游的某个部位遭遇分离激波,流动与壁面发生分离,其后变为自由射流状态。在流动分离点下游,外界环境气体会从喷管和射流之间的空隙涌入,并形成贴壁的漩涡。其壁面压强分布的特点是:从喷管喉部开始,先逐渐降低,在分离点附近达到最小值,而后迅速升高到接近但低于环境压强的水平,随后缓慢上升到环境压强。
图1和图2中NPR≤17.61的四条压强分布曲线均符合这一特点。为了进一步确定该阶段确实发生了自由激波分离,采用数值方法复算了这一阶段的工况。
计算方法和边界条件的设置参考了文献[7],采用有限体积法,对流项为二阶迎风格式,粘性项中心差分,湍流模型为Spalart-Allmaras一方程模型。
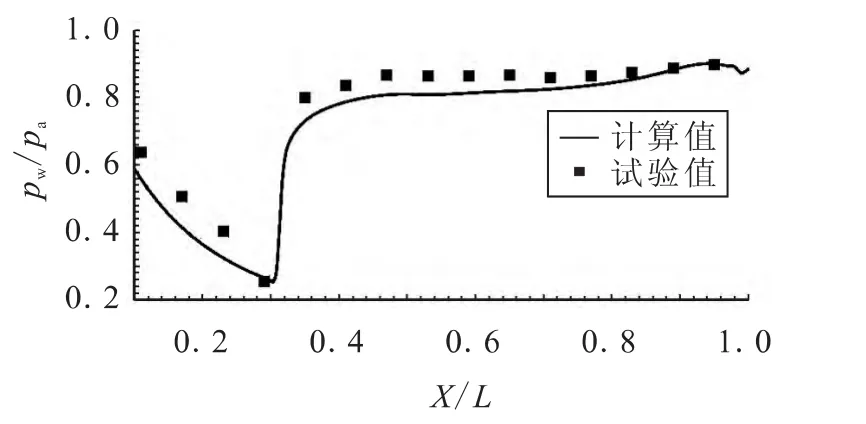
图3 NPR=15.78时的壁面压强分布曲线Fig.3 Curves of wall pressure distribution as NPR=15.78
图3对比了试验和数值计算获得的壁面压强结果。计算值略低于试验值,最大误差约为5%,整体趋势一致,而且分离点的位置相符度很好。
图4直观地显示了在该喷管压比下流动就是自由激波分离,图中速度发生剧烈变化的面就是分离激波系。
随着NPR升高,分离点会逐渐向下游移动,分离点附近存在巨大的压强梯度。如图1所示,四个自由激波分离的工况中,指示分离点位置的高压强梯度随着室压的升高而向下游推移,直到分离模态发生变化。
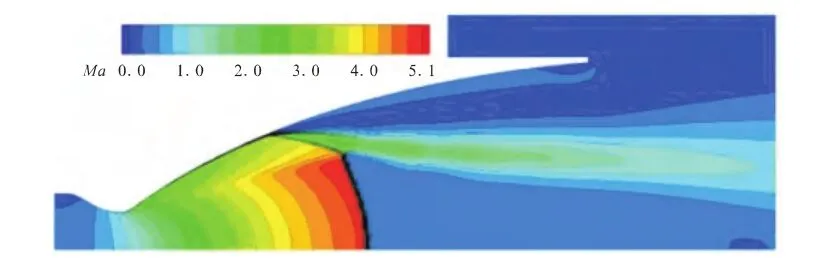
图4 NPR=15.78时的马赫数云图Fig.4 Cloud chart of Mach number as NPR=15.78
2.3.2 受限激波分离
在TOP喷管中,当NPR达到一个临界区间时,流动分离模态开始从自由激波分离转变为受限激波分离。
自由激波分离模态下分离激波后的自由射流会在分离线下游接近喷管壁面,此前可供外界气体涌入的缝隙被堵住,流动从壁面分离后又在下游重新贴合到壁面,从而形成一个有限大小的分离腔。值得注意的是在自由激波分离向受限激波分离切换的瞬间,虽然NPR增加并不显著,但同一母线上分离点的位置却会向下游跳跃,这段距离十分显著。本试验中各个工况的NPR间隔基本在2.5左右,相同分离模态相邻工况之间分离点的推进距离基本在0.05 X/L左右,只有在自由激波分离向受限激波分离转变的NPR间隔内推移距离达到了0.2 X/L的量级。试验数据显示这种转变发生在17.61≤NPR≤18.49的压比范围内,分离位置在x=0.5 X/L附近。
受限激波分离在流动重新贴合到喷管后与满流情况下的贴壁流动有显著不同,壁面压强不是平滑下降而是剧烈波动,试验测得受限激波分离情况下壁面压强的峰值达到了1.64 Pa,见图5。
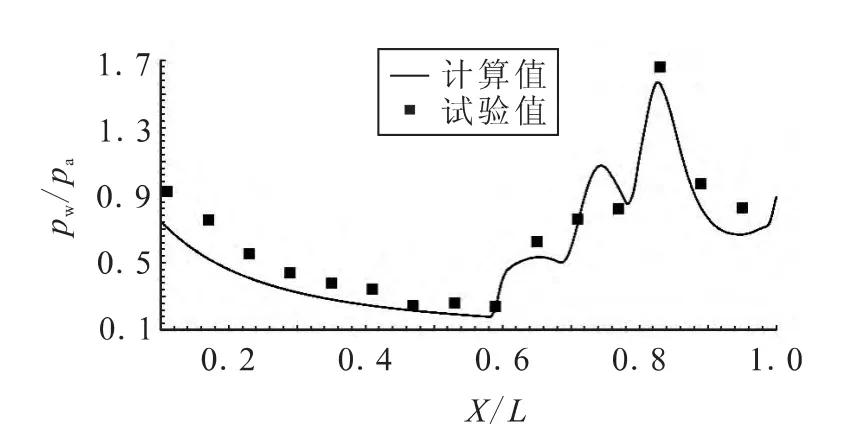
图5 NPR=20.18时的壁面压强分布曲线Fig.5 Curves of wall pressure distribution as NPR=20.18
图5给出了NPR=20.18时的壁面压强试验值与计算值对比。同NPR=15.78的情况类似,整体趋势一致,但计算值总体上略低于试验值。

图6 NPR=20.18时的马赫数云图Fig.6 Cloud chart of Mach number as NPR=20.18
图6显示了NPR=20.18时的流速分布,从图中可以明显看出流动从壁面处分离后又在下游重新贴合到壁面,而图5中的压强值则证明了这种贴合不同于满流状态下的贴壁流动。这种区别的原因在于受限激波分离模态下特有的波系结构,从壁面处分离出来的超声速气流在下游反复撞击壁面,从而导致沿母线压强的反复波动。
3 试验误差分析
壁面压强测量所采用的传感器精度为±0.2%。根据试验获得的数据,可以认定传感器的响应频率可以用于测量本试验中的稳态压强。
同样地,由于本试验为稳态测量试验,软管的长度不超过1 m,采用可压缩气体“线性摩擦管道模型”计算出的最低共振频率为82 Hz,误差不超过5%,可以满足静压测量的要求。此前有不少同类试验都采用了软管测压的方式,文献[8]即采用了这种设计,也说明该方法可以用于本试验的压强测量。
采集系统采用3总线光电隔离技术,使被测信号系统与计算机之间完全电气隔离(隔离电压大于500 V),具有较高的输入阻抗和共模抑制比,其采样最高频率为66 kHz,其系统综合误差为±0.2%FSR。
测量系统总体测量精度为1.0%。响应频率可以支持本试验中的稳态工况测量。
4 结论
1)大膨胀比TOP喷管在地面试车时,随着工作压强比升高,确实会依次经历自由激波分离和受限激波分离。
2)试验中采用的TOP喷管构型下,自由激波分离向受限激波分离的转变发生在17.61≤NPR≤18.49的压比范围内。分离位置在x=0.5 X/L附近。
3)试验中采用的TOP喷管构型下,受限激波分离时壁面压强峰值为1.64 Pa。
[2]NAVE L H,COFFEY G A.Sea level side loads in high-area-ratio rocket engines[C]//9th AIAA/SAE Propulsion Conference.New York:AIAA,1973,11:1-66.
[3]BAARS W J,TINNEY C E,RUF J H,et al.Wall pressure unsteadiness and side loads in overexpanded rocket nozzles[J].AIAA Journal,2012,50(1):61-73.
[4]WATANABE Y,SAKAZUME N,TSUBOI M.LE-7A engine nozzle problems during the transient operations[C]//38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Indianapolis,Indiana:AIAA,2002(July):1-6.
[5]TERHARDTM,HAGEMANNG,FEYM.Flow separation and side-load behavior of the Vulcain engine[C]//35th AIAA/ASME/SAE/ASEE JointProptiMon Conference&Exhibit.Los Angeles,California:AIAA,1999(C):1-12.
[6]李波.液体火箭发动机喷管分离流动的数值仿真及实验研究[D].北京:北京航空航天大学宇航学院,2013.
[7]胡海峰,鲍福廷,蔡强,等.大膨胀比火箭发动机喷管流动分离与气动弹性分析[J].固体火箭技术,2011,34(6):711-716.
[8]RUF J H,MCDANIELS D M,BROWN A M.Details of side load test data and analysis for a truncated ideal contour nozzle and a parabolic contour nozzle[C]//46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit.Nashville,TN:AIAA,2010:111-118.

