尾矿坝坝料的动力特性研究

王庆满

(机械工业勘察设计研究院有限公司，陕西 西安710043)

尾矿坝是一种特殊的水工建筑物，尾矿坝坝料具有含水率高、土质疏松、抗变形和抗液化能力弱、自振周期长等特征，并且大多数尾矿坝都采用上游法筑坝，其更不利于尾矿坝的抗震[1]。尾矿坝的运营好坏，直接影响到矿山企业的经济效益及库区下游居民的生命财产安全。一旦发生地震，后果往往触目惊心。例如，1965年智利 7.25级地震中 12座尾矿坝不同程度发生破坏，造成 270人死亡[2];1986年 4月30日，安徽黄梅山尾矿库发生溃坝，19人死亡，100人受伤;2008年9月8日，山西省临汾市襄汾县新塔矿业有限公司尾矿库溃坝，276人死亡，直接经济损失 9619万，并造成严重环境污染[3]。尾矿坝坝料的动力特性直接影响着尾矿坝的稳定性，许多学者对此进行了相关方面的研究[4－6]。本文以陕西某矿为依托，研究其坝料动力特征，为同类型尾矿坝的抗震稳定性分析提供借鉴和参考。

1 尾矿坝坝料的物理力学性质特征

尾矿坝是由尾矿渣沉积形成的，由于放矿支管的不规律放置，使其冲击体呈现粒度粗细交替的变化特征。根据尾矿坝岩土工程勘察报告，本尾矿坝坝料以尾粉质粘土为主，局部夹薄层尾粉土及尾粉砂。

本次试验取样深度分别为 5 m、9 m、13 m、20 m、34 m，个别土样含薄层粉砂，其基本物理力学指标见表1。

表1 试样基本物理力学指标

由表1可以看出，坝料含水率、天然密度及饱和度随深度规律性不明显，不同深度出现拐点，说明其矿物成分及物质组成的不均匀性，按《岩土工程勘察规范》(GB 50021－2001)(2009年版)分类，该尾矿库坝料属于低塑性的粉质粘土。

2 动三轴试验

2.1 实验仪器

本次试验仪器为英国进口GDS高精度双向振动三轴仪，其基本工作原理是利用高速直流伺服马达施加轴向和径向的动荷载，根据电子荷重传感器和位移传感器的反馈对荷载和变形的大小进行计算机控制。可适用于 38、50、70、100 mm直径的试样。

2.2 试样制备

本次土样均采用敞口薄壁取土器静压取土，试样尺寸:φ50 mm ×h100 mm。

2.3 试验方案

本次动三轴试验在固结应力比 Kc=σ1/σ3=1条件下进行，围压分别设定为 100 kPa、200 kPa、300 kPa，采用应力控制等效正弦加载方式，频率为1 HZ，振动中心(datum):(σ3+σd)/2。

加荷过程:首先采用GDS的高级加载模块给试样施加预定围压，调节刚度系数，之后逐级施加动荷载，每级荷载循环震动10次，直到应力 －应变曲线出现峰值，若无峰值出现，一般以累积应变 εd=5%作为试验终止条件，本次为研究不同应变标准下(3%、5%、7%)的动强度变化特征，则以 εd=8%作为试验终止条件，动力幅值见表2。

3 试验结果与分析

3.1 动模量

动弹性模量是研究土动力特征的重要参数，它表征土体在弹性变形阶段的动应力与动应变关系。可近似的依据滞回圈顶点连线的动应力σd和动应变εd，计算动弹性模量Ed。

表2 动应力幅值设定表

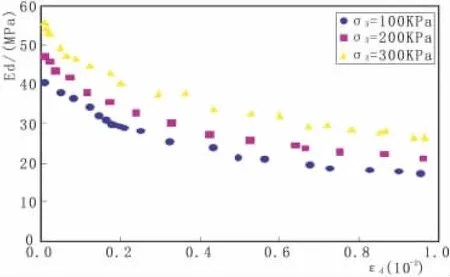
图1 不同围压下 Ed与εd关系

图1 为不同围压下动弹性模量Ed与动应变 εd关系曲线图，以5 m试样为例，其它试样变化规律与其相似，此处不在详述。结果表明:1)动弹性模量Ed随着动应变εd的增加而急剧递减，递减速率先快后慢;当动应变小于10－3时，动弹性模量 Ed与动应变 εd呈近线性变化，当 εd=10－3～10－2时，动弹性模量Ed随应变εd递减速率减慢，当εd=10－2时，动弹性模量Ed约递减为初始值的50%。2)在不同围压 σ3(100 kPa、200 kPa、300 kPa)条件下，动弹性模量 Ed与围压 σ3呈正相关性，围压每增加一级，动弹性模量 Ed增加约20%。

Hardin等人认为循环荷载作用下土的动应力－应变关系可用双曲线表示[7－8]。

令 1/E0=a，1/σy=b，所以动弹性模量可表示为:

图2 不同围压下1/Ed－εd拟合关系曲线

图2 表明1/Ed～εd呈现良好的线性关系，拟合度较高，其中，a为截距，b为直线斜率。因此，动弹性模量与动应变关系也可用双曲线模型表示。

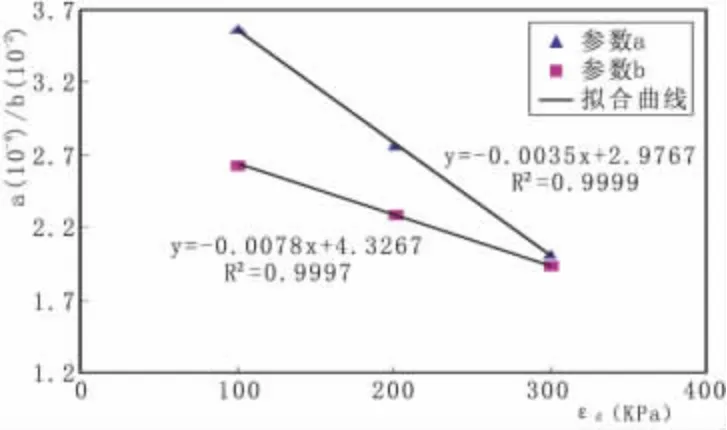
图3 参数a、b与围压的关系曲线

由图3中的拟合方程可以看出参数a、b均随着围压的增大而减小，因此对其进行线性拟合，如图4，即有:

3.2 阻尼比

阻尼比是研究土动力特征的另一个重要参数，它表征土体循环荷载循环一周所消耗能量的多少，反映了土体应力应变关系的滞后性。它的计算方法由应力应变滞回圈的面积来确定。

式中:AO为滞回圈面积;Ar为滞回圈顶点与X轴及原点围成的三角形面积。

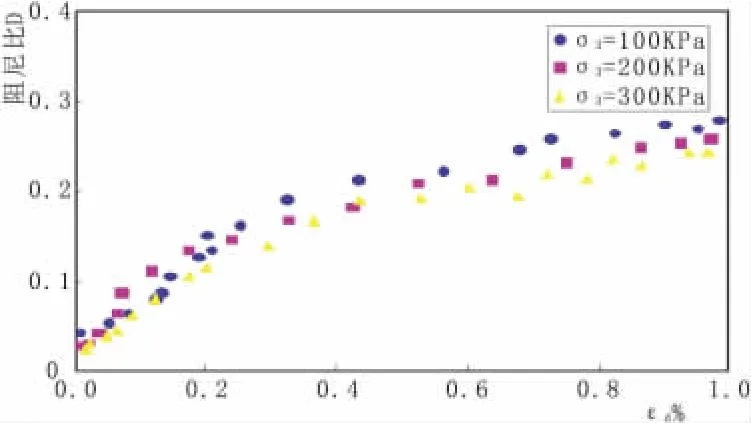
图4 阻尼比λ与εd关系

图4 表明:1)阻尼比λ随着动应变 εd的增大而增大，当动应变εd很微小时，阻尼比λ几乎接近于零，随着动应变 εd的增大，阻尼比 λ 明显增大，当 εd=0～10－3时，阻尼比 λ 随着动应变 εd的增大迅速攀升，当 εd=10－3～10－2时，特别是εd＞3×10－3后，阻尼比 λ增大的趋势明显放缓，曲线变得逐渐平缓，随着εd的继续发展，阻尼比渐进于某一常数，达到最大值，即 λmax。2)围压阻尼比 λ随着围压 σ3的变化略有变化，围压升高，曲线略有降低，即阻尼比λ随着围压的升高略有减小。在微小动应变时，表现的不是很明显，当 εd＞3×10－3时，表现的越明显;当 εd=10－2时，围压每增加一级，阻尼比减小约5%～10%。

图5 试样破坏形态

3.3 动强度

动强度是试样在动荷载作用下达到指定破坏应变所需的动应力。破坏应变由破坏标准来确定。破坏标准分为三种:应变破坏标准、极限平衡破坏标准、孔压标准。等压固结条件下非饱和土的循环动三轴试验中孔隙水压力和孔隙气压力同时存在，而该条件下试样主要产生轴向应变(如图5)，因此比较适合采用应变破坏标准。一般采用以应变5%作为破坏标准，具体以工程性质而定。本次选用 εd=3%、5%、7%作为破坏应变，讨论不同应变标准下坝料的动强度特征。

在等压固结条件下，分别逐级施加动应力，直到试样达到破坏应变为止，表3表明，不同应变标准下，动强度随应变标准的增大而增大;同一应变标准下，动强度也随围压的增大而增大，二者呈现较好的线性拟合关系，拟合度较高，见图6。

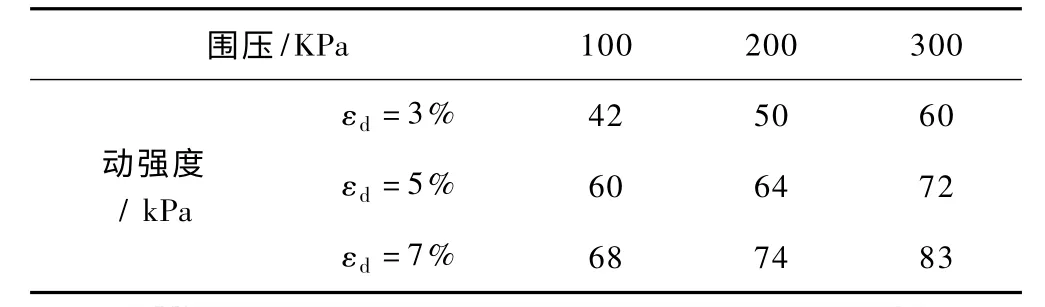
表3 不同应变标准下尾粉质粘土的动强度

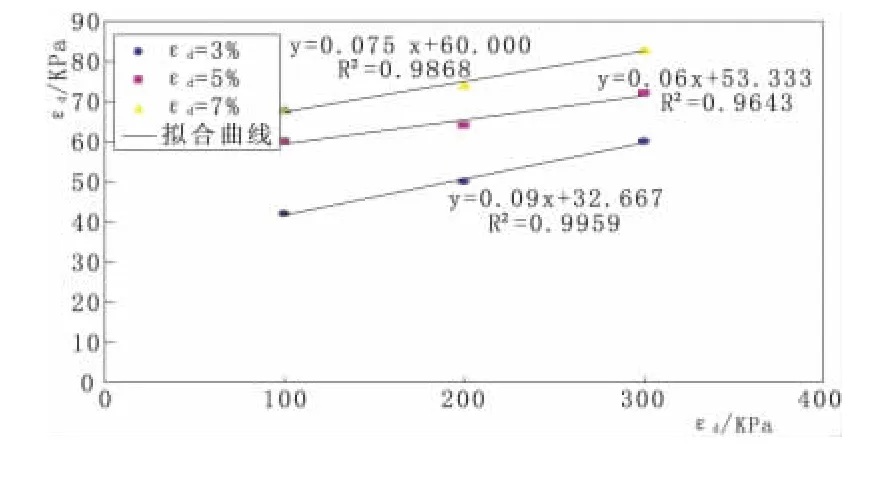
图6 动强度与围压及应变标准的关系曲线

Cd、φd是动三轴试验中评价土体动强度的重要定量指标。在相同实验条件下，分别确定试样在三种围压下的主应力 σ1、σ3，依据摩尔库伦破坏准则，绘制 3个应力摩尔圆，再根据这3个应力摩尔圆绘制它们的动抗剪强度包络线，从而得到该动应力下的动抗剪强度指标Cd、φd。本次5组试样的动强度指标结果见表4。

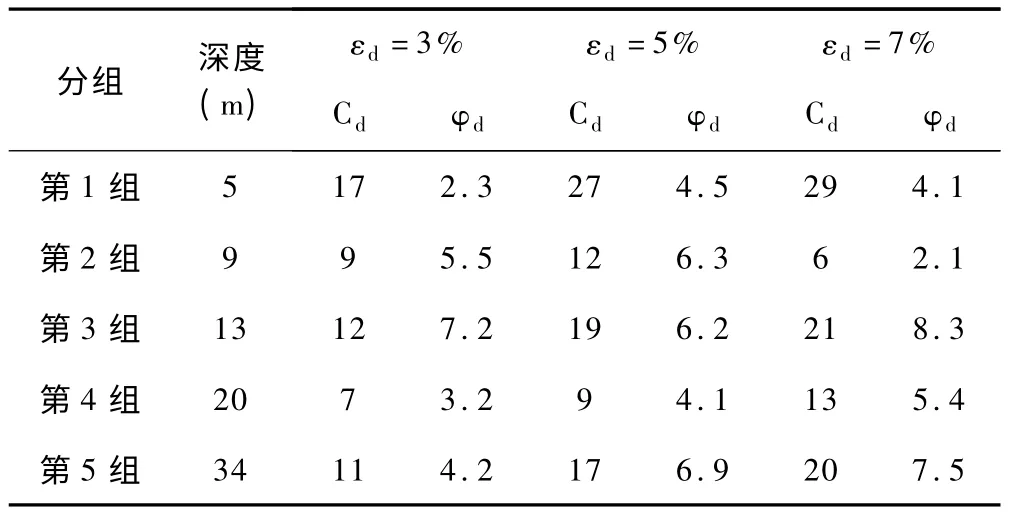
表4 不同应变标准下试样的动强度指标

图7 粘聚力随深度关系曲线

表4表明，1)动强度与破坏应变标准息息相关，在一定的应变范围内，随着破坏标准的增大，粘聚力与内摩擦均增大，粘聚力的变化幅值大于摩擦角变化幅值。

2)从图5及表4中可以看出，相同试验条件下，第二组试样发生了明显的剪切破坏，动强度指标先增大后减小，其原因在于试样在 εd＞5%之后产生了明显剪切破坏面，试样破坏，其εd=7%时的指标为残余强度指标。

3)坝料的动强度指标较低，与其静强度相比(见表2－4，图7－8)，粘聚力与内摩擦角均有所减小;且动强度指标与取样深度的相关性不明显。这是由于尾矿坝是在水力分级作用下形成的，尾矿坝沉积层具有各向异性，其结构强度随尾矿类型、沉积方式、时间和空间而变化。总体而言，其自身的结构强度较低，因此，在循环荷载作用下，土体结构容易遭到破坏，导致其强度降低。

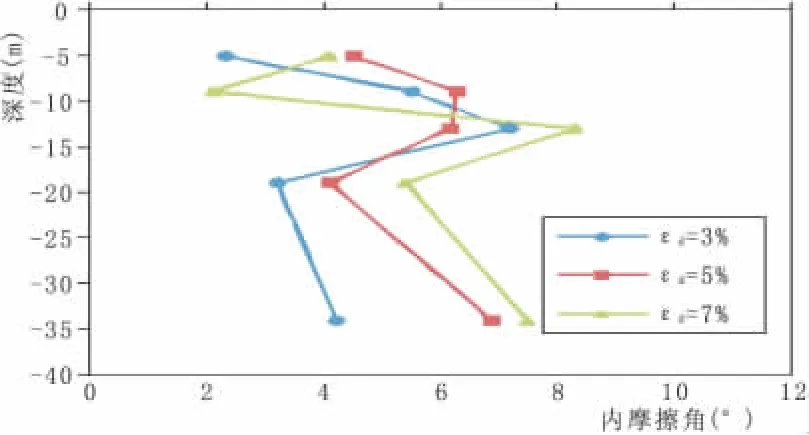
图8 内摩擦角随深度关系曲线

4 结语

本文基于GDS动三轴试验系统，对尾矿坝坝料动力特性进行试验研究，初步得出以下结论:

(1)动弹性模量Ed随着动应变 εd的增加而急剧递减，递减速率先快后慢;动弹性模量 Ed与围压 σ3呈正相关性，围压每增加一级，Ed增加约20%;动弹性模量与动弹性应变之间关系可用双曲线模型来表示，并总结出了围压对模型参数的影响规律。

(2)阻尼比λ随着动应变 εd的增大而增大，增大速率先快后慢，随着εd的继续发展，阻尼比λ渐进于某一常数，达到最大值，即λmax。阻尼比λ随着围压的升高略有减小，在微小动应变时，表现的不是很明显，当 εd＞3×10－3时，表现的越明显。

(3)动强度与破坏标准息息相关，在一定的应变范围内，动强度指标随应变标准的增大而增大，其中粘聚力的变化幅值大于摩擦角变化幅值;坝料的动强度指标较低，与其静强度相比，粘聚力与内摩擦角均有所减小，且动强度指标与取样深度的相关性不明显。

(4)由于尾矿坝坝料是一种具有特殊工程性质的土，因此，在进行尾矿坝抗震稳定性分析时，必须对其地层特征及物理力学指标进行详细的分析计算并建立合理的力学数学模型。

[1]王凤江.上游法高尾矿坝的抗震问题[J].冶金矿山设计与建设.2001(5):10–13.

[2]Anon. A review of dam tailings dam failures.International Water Power，2001，53(5):40 ～ 42.

[3]彭承英.尾矿库事故及预防措施.有色矿山.1996，5:38－40.

[4]贺汇文，龙建辉，吕远强.米箭沟尾矿坝料动力特征试验研究[J].工程地质学报.2007，15(06):0817－0822.

[5]陈敬松，张家生，孙希望.饱和尾矿砂动强度特性试验结果与分析.水利学报.2006:37(5).

[6]刘宪权，谢孔金.基于尾矿坝坝体沉积尾矿的动强度特征[J].西部探矿工程.2006，09:0051 －0053.

[7]谢定义.土动力学[M].西安:西安交通大学出版社.1988.

[8]吴世明，周景星.土的动力特性及测试和应用[A].见:第 3届全国土动力学学术会议论文集[C].上海:同济大学出版社.1990.