基于遗传BP神经网络的地下水位预测模型

许 骥

(新疆水利科技推广总站，新疆 乌鲁木齐830000)

地下水水位变化与土壤剖面盐分运移、农田土壤盐渍化演变、水资源开发利用模式等均有密切联系，因此地下水水位动态预测对农田土壤盐渍化防治、地下水地表水资源的合理调度都具有十分重要的意义。BP神经网络模型在分析处理非线性数据方面效果颇佳，可有效表明具非线性关系的输入量与输出量的关联性。但在实际应用中BP神经网络呈现出网络全局搜索能力不足、迭代收敛缓慢和局部最优的缺陷。使用遗传算法优化BP神经网络模型的连接权值后，可提高BP神经网络的训练速度，克服了网络易陷入局部极小［1］。

鉴于此，本文在前人研究的基础上，以新疆和静县某地下水观测井为研究对象，从影响地下水水位的蒸发量、气温和灌溉量入手，采用BP人工神经网络预测方法，建立研究区地下水位预测的遗传BP神经网络模型。为指导当地地下水资源的开发利用与保护及盐碱地治理提供理论基础。

1 BP神经网络模型结构的设计

1986年，由斯坦福大学的D E Rumelhart等提出的BP神经网络算法，解决了多层网络模型中隐含层的连接权问题，有效提升了神经网络的自学习和组织能力，是当前工业领域应用较多的一种前馈式学习算法与反向传播算法的神经网络［2，3］。BP神经网络的输入层由隐含层作用于输出层，经非线性变换得输出量。网络训练的每个样本包含输入量和期望输出量，网络输出量与期望输出量之间的偏差，通过调整网络权值与阈值，使误差沿梯度方向下降，直至实际输出与期望输出在预定范围内。

设输出层有m个神经元，BP网络的实际输出是y;期望输出是y';函数ε为:

每个权值的修正值为:

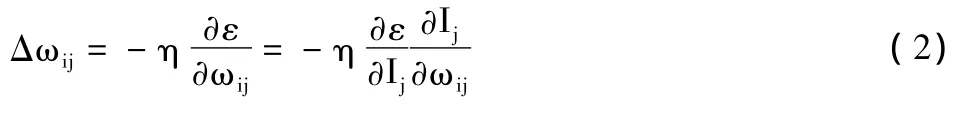
式中:ωij为输入单元i到隐含层单元j的权重;η是学习速率，Ij是中间第j个隐含层的传输函数。输入层到隐含层的函数采用Logsig型，隐含层到输出层的函数采用Purelin型。

由于影响地下水位的主控因素是蒸发量、气温和灌溉量，设定此3因素做为神经网络模型的输入参数，确定输入端点数为3。据查，BP神经网络的输入节点为u时，网络的隐含层节点数选取2u+1时，BP网络模型能很好反映实际［4］，故隐含层节点数为7个。据此，该 BP网络模型采用3层网络，BP结构为3－7－1，网络结构图如图1所示。

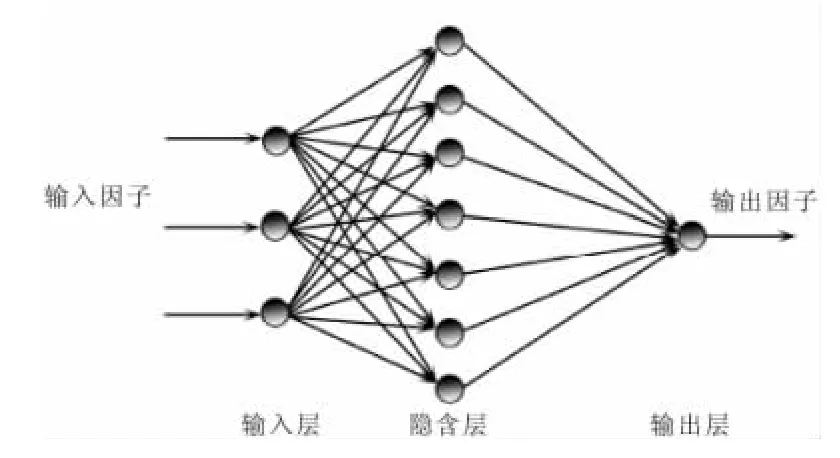
图1 BP神经网络模型拓扑

2 遗传优化BP神经网络模型

遗传算法擅长全局搜索，BP神经网络在用于局部搜索较有效，故遗传算法和BP算法相结合颇为有效。遗传算法对神经网络初始权值进行优化，定位出较好的搜索空间，再采用 BP算法在小空间内搜索最优值［5］。改进后的遗传算法流程图如图2。

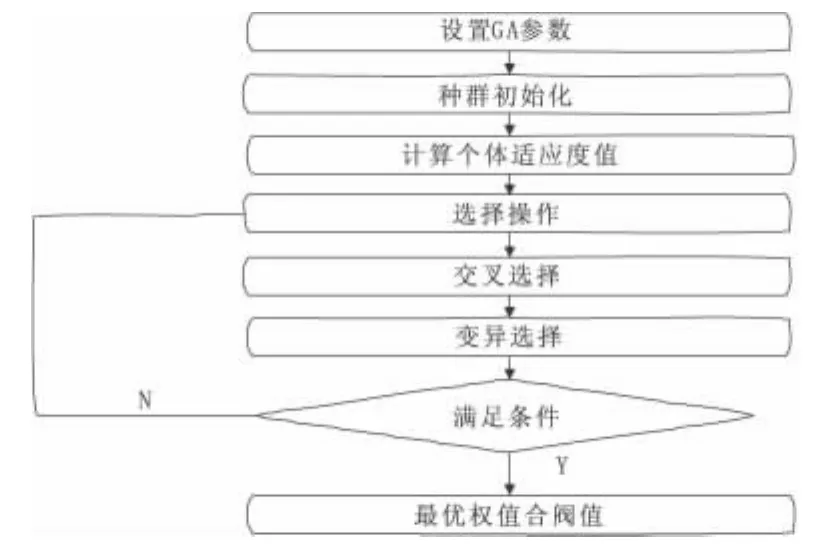
图2 改进遗传算法流程图

改进后的遗传算法具体步骤如下:

1)初始化种群。随机产生一种群Xm×n，每个个体X1×n代表一个神经网络的初始权值分布，每个基因值为一个连接权值，则个体的长度为神经网络权值的个数，即:

式中:n为个体的长度;r为输入层节点数;s1为隐含层节点数;s2为输出层节点数。

选择浮点数编码方式对权值编码。

2)适应度函数依据适应度函数值对个体进行评价，对每一个体解码得到BP神经网络输入样本，计算输出误差值E，适应度函数f。

计算各个体的适应值，种群个体适应度最大者进入子种群。

3)选择算子。采用轮盘赌法选择算子。设第i个个体的适应值fi，则被选中的概率为:

式中:m为种群规模，m=50。

4)交叉算子。交叉算子选择算术交叉，由两个个体的线性组合出两个新的个体。假设在两个个体Xi(k)、Xi+1(k)之间以交叉概率pc进行交叉操作，则交叉后产生的两个新的个体是

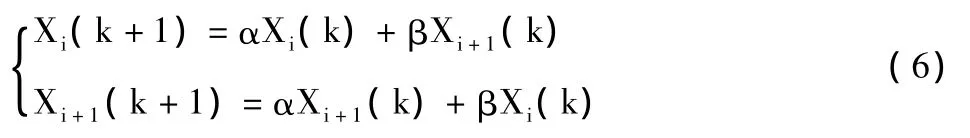
式中:Xi(k)、Xi+1(k)分别表示第i和第i+1个个体在第k位的基因;α、β是0～1之间的随机数。

5)变异算子。选择均匀变异算子，对每一基因值，以变异率pm对应的基因取值域取一随机数进行替换。

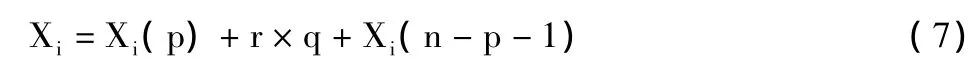
式中:q为第p+1个基因值对应的阈值宽度。

6)计算适应度函数值。计算适应度函数值，判断是否达到最大迭代次数或满足精度要求，否则返回第2步。

遗传完成后，取遗传算法中得到的最优个体作为神经网络的初始权值，通过给定样本数据，按BP算法对神经网络训练，求出最优解。

3 结果与分析

本研究数据主要来源于新疆和静县某地下水观测井2008年1月－2013年12月间的地下水水位、同期蒸发量、气温与灌溉量等时序监测数据，各类数据的监测频率为每1次/d(其中，地下水水位为每半月1次)，本研究采用的为各月平均值数据。采用2008年1月－2012年12月共60个月的地下水水位监测数据与气象数据作为模型训练数据，2013年1月－2013年12月共12个月的数据则用作模型预测的验证数据。

月均蒸发量、气温与灌溉量这3项为网络学习样本中的输入因子，输出因子为实测地下水水位。网络学习样本数据先归一化，再经多次迭代，使试验数据的网络训练误差值逐步收敛。

遗传算法通过随机问题假设集合，根据适应度函数对个体进行数值评价，遗传算子模拟遗传过程中出现的复制、交叉和变异现象，对种群个体择优。遗传算法对BP网络初始权值和阈值进行优化赋值，再利用BP神经网络预测模型进行局部寻优。遗传算法进化过程中设置种群数目为50，进化代数为100，交叉概率为0.5，变异概率为0.09。根据上述遗传BP神经网络模型，通过Matlab软件编程，可得经实数遗传算法优化后的BP神经网络各层之间权值和阈值，如表1所示。

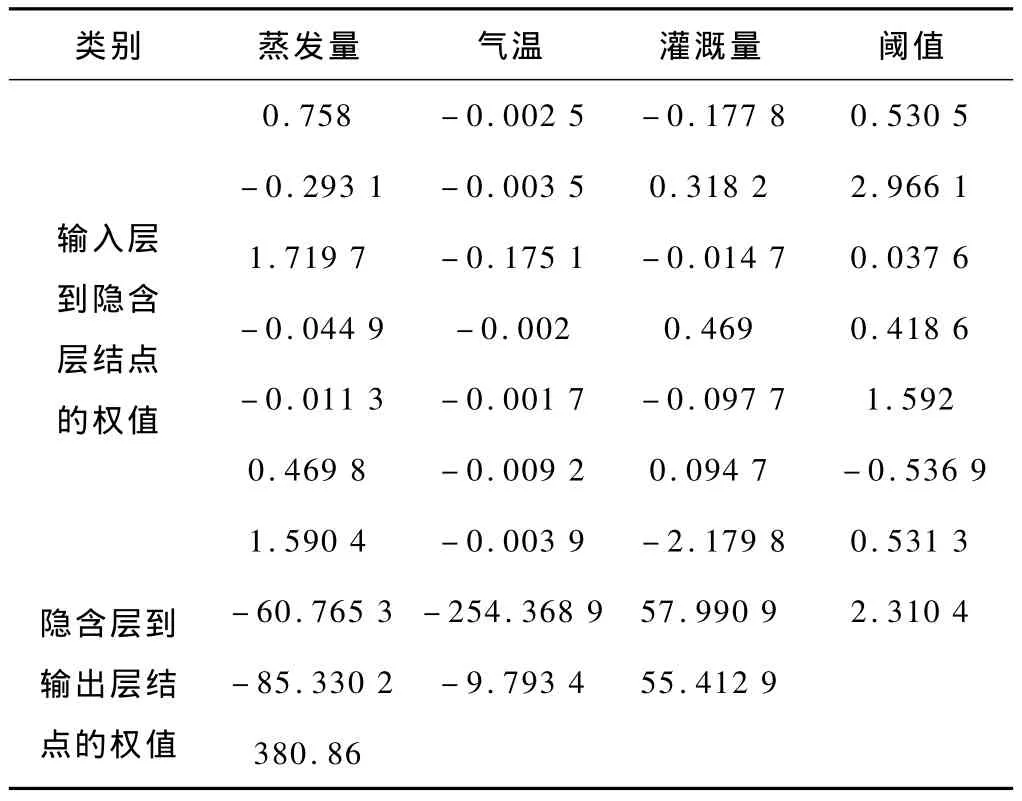
表1 遗传BP神经网络的各主控因素系数

图3为利用BP神经网络模型与遗传BP神经网络模型得到的地下水位预测值。由图3可知，依据地下水位变化的主控因素所建立的两神经网络模型，其地下水位预测值与实测值基本吻合。采用平均绝对百分比误差(MAPE)、均方根误差(MSE)和平均绝对误差(MAE)3个特征指标进行比较，各类指标值越大则表示预测值与实测值偏差越大［6］。各统计指标结果见表2。由表2可知，经遗传法优化的BP神经网络模型的拟合效果要优于BP神经网络模型。

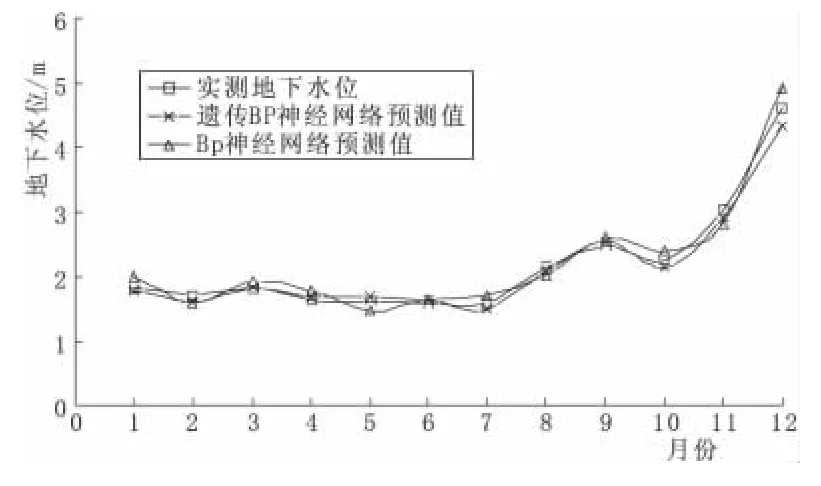
图3 地下水位预测值与实测值对比(2013年)

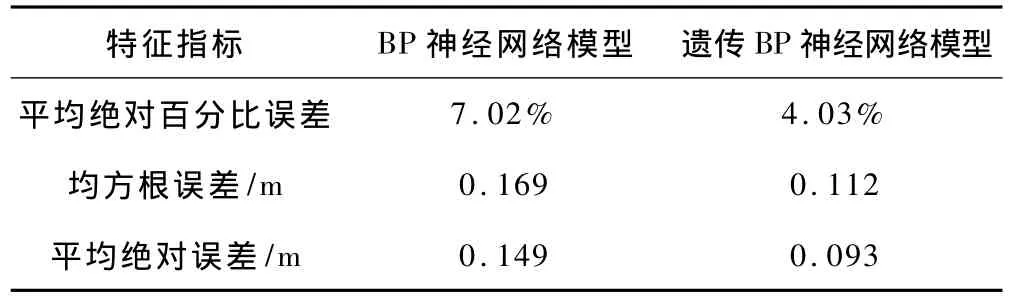
表2 2种模型预测结果评价

图4为遗传BP神经网络模型测试样本的网络输出值Y和网络目标值X的回归直线。网络输出值Y是用训练后的遗传BP神经网络模型计算得出输出值。网络目标值X是遗传BP神经网络训练所要实现实测值。由图4可知，回归直线的相关系数R为0.967 3，近似为1。另，回归直线与斜率为1的直线(Y=X)基本重合，表明遗传BP神经网络的输出值与其目标值偏差极小，是非常有效的预测方法。

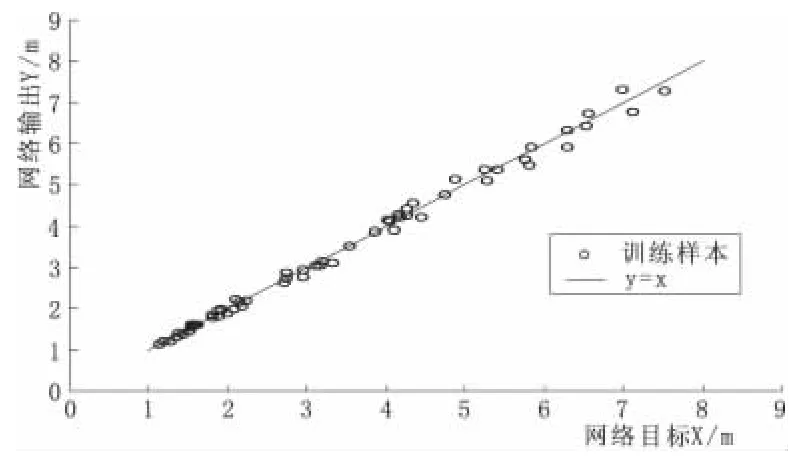
图4 训练样本输出回归直线

4 结语

(1)建立了一个用于预测地下水水位的遗传BP神经网络模型，测试样本的网络输出值与网络目标值的相关系数达0.967 3，表明所建立的网络模型是有效的。

(2)用BP神经网络模型和遗传BP神经网络模型对12组未参加建模的样本数据(2013年数据)进行预测。预测结果表明，遗传BP神经网络模型的平均绝对百分比误差、均方根误差和平均绝对误差3个特征指标值均小于BP神经网络模型的指标值，表明遗传BP神经网络模型预测拟合效果远优于BP神经网络模型。

(3)地下水水位与其影响因素存在着复杂的非线性关系。本文所建立的基于遗传BP神经网络的预测模型可作为地下水动态变化预测的新方法，这为区域地下水的开发利用与保护提供了参考依据。

［1］王德明，王莉，张广明.基于遗传BP神经网络的短期风速预测模型［J］.浙江大学学报:工学版.2012，46(5):837－841，904.

［2］刘厚林，吴贤芳，王勇.基于BP神经网络的离心泵关死点功率预测［J］.农业工程学报.2012，28(11):45－49.

［3］张建华，祁力钧，冀荣华.基于粗糙集和BP神经网络的棉花病害识别［J］.农业工程学报.2012，28(7):161－167.

［4］孟召平，田永东，雷旸.煤层含气量预测的BP神经网络模型与应用［J］.中国矿业大学学报.2008，37(4):456－461.

［5］吴建生，金龙，农吉夫.遗传算法BP神经网络的预报研究和应用［J］.数学的实践与认识.2005，35(1):83－88.

［6］杨永生，何平.投影寻踪回归与BP神经网络方法在前汛期降水预测中的比较研究［J］.气象与环境学报.2008，24(1):14－17.