幂和公式系数L7,3≠291

文 萍

(玉溪师范学院理学院,云南玉溪653100)

幂和公式系数L7,3≠291

文 萍

(玉溪师范学院理学院,云南玉溪653100)

幂和公式;系数值;李善兰数

研究了自然数幂和公式中的系数值问题,并对文献[1～3]存在的个别问题及系数L7,3的取值错误进行求正.

众所周知,所谓“幂和公式”是指求自然数的前n项方幂和的公式,这是一个古老的问题,具体例子也已多见.其一般形式由我国清代数学家李善兰首先完整给出,用现代形式表示如下：(1)式中的Lp,i就称为李善兰数[1,2].文献[2]和文献[3]中都给出了Lp,i的数值表.而通过研究,笔者可以发现其中的L7,3≠291,下面详细说明推导方法.

当p=7时,

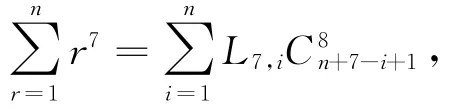
也就是：

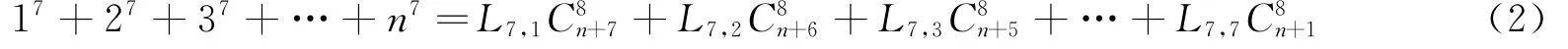
从文献[2]和文献[3]给出的Lp,i的数值表,具体到L7,i为：

而对于L7,3=L7,5≠291,我们可以从以下三个角度来来进行判定：

其一：取n=1,利用上面的公式(2),有：

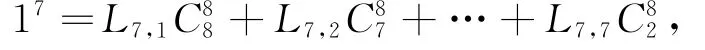
其中,Cmn当n＜m时均定义为0,即L7,1=1.

再取n=2,有

即129=C89+L7,2,得7,2=120.

现取n=3,有

也就是2316=45+120×9+L7,3,于是可得L7,3=L7,5=1191.所以说,李善兰数L7,3=L7,5≠291.

其二：根据李善兰数的递推公式

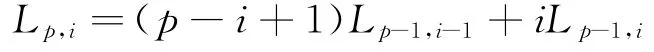
可知

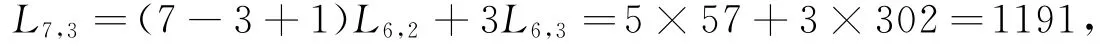
相应的

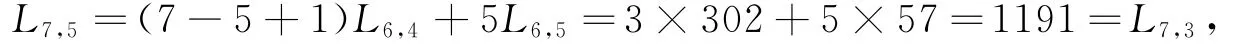
还可以从L8,3=(8-3+1)L7,2+3L7,3算得L7,3=1191.

其三：观察文献[2]、[3]给出的李善兰数值表,当i＞1时Lp,i都是关于p的递增数列,为何对于Lp,3却有：1,11,66,302,291,4 293,14 608,…,即其中L6,3=302,L7,3=291,突然呈下降趋势,显然与递推公式的变化态势有矛盾.

而对于上述错误,由于笔者所掌握的资料有限,很难对其原因进行详尽的考证,但根据文献[1]提供的图表4-9、4-10、4-11、4-12等的写法,笔者猜测,其是否是将中文大写的“一一九一”当成291所致.

另外还要说明的是,文献[3]第197页第2行的递推公式也有错,等式右端第一项里的Lp-1,j应为Lp-1,j-1,表1-5中的L5,4=20也是错的,应为L5,4=26.

[1]李迪.中国数学史简编[M].沈阳：辽宁人民出版社,1984.

[2]汪晓勤,韩祥临.中学数学中的数学史[M].北京：科学出版社,2002.

[3]沈康身.数学的魅力：(四)[M].上海：上海辞书出版社,2006.

The Coefficient of the Formula of the Sum Powers L7,3≠291

WEN Ping
(School of Science,Yuxi Normal University,Yuxi,Yunnan 653100,China)

the Formula of the Sum Powers;coefficient;Li Shanlan Numbers

In this paper,the coefficient of the Formula of the Sum Powers was studied and some problems in Documents 1～3 and the errors in the coefficient L7,3were corrected.

文 萍,硕士,讲师,研究方向：数学教育和代数学.

O157.1

A

1009-9506(2015)08-0039-02

2015年5月9日