基于自适应算法的月球引力常数和J2系数确定

王 祎，杏建军，郑黎明，于 洋

(中南大学航空航天学院，长沙410083)

0 引言

月球引力场的高精度测量对研究月球演化和开展月球探测具有重要意义，因此成为国际深空探测领域研究的热点。然而由于月球自转周期和公转周期同步，导致月球始终只有一个面朝向地球，因此月球背面引力场数据很难用传统方法测量，这也是高精度月球引力场模型建立所面临的最大技术难题。Konopliv 等［1］、Matsumoto 等［2］和 Goossens 等［3］国内外学者也对高精度月球引力场模型的建立做了众多的研究:Konopliv采用了美国的GRAIL［4］的月球引力场测量数据恢复月球引力场，月球引力常数精度达到4.90280031 ×1012±4.4 ×105m3/s2，其中J2项摄动系数精度为 9.0880835 ×10－5±1.4 ×10－9;Matsumoto和 Goossens则是分析了日本的SELENE［5］计划的月球引力场的测量数据后得到精度为4.90280080×1012±9×105m3/s2的月球引力常数;利用环月飞行的月球探测器之间卫卫跟踪测量辅助地面深空探测网进行月球引力场确定，是现今直接测量月球背面引力场的唯一方法，日本SELENE计划和美国GRAIL任务分别应用这种方法进行了月球背面引力场的测量，有效地提高了月球引力场测量的精度。

Psiaki［6］提出了一种基于星间相对位置测量信息自主确定月球引力场的方法。该方法利用两颗环月编队飞行的卫星构成一个独立自主的测量系统，环月编队飞行的卫星在不依赖地面深空探测网支持的条件下，利用编队卫星星间相对位置的测量数据，采用扩展卡尔曼滤波器(Extend Kalman Filter，EKF)滤波算法，自主确定月球卫星轨道，同时修正月球引力场参数，得到更高精度月球引力场模型。

考虑到实时导航要求，Psiaki［6］采用实时性较强的EKF算法，且EKF算法在处理白噪声激励下的平稳或非平稳向量的状态估计问题时能够得到最优的结果［7］。然而在实际应用中，EKF的动力学模型和观测模型不可能准确无误，系统噪声和测量噪声特性不能提前精确确定，导致状态参数估计精度的降低，甚至滤波器的发散［8］。

针对EKF算法中的系统噪声或者测量噪声难以精确确定导致滤波器精度降低的问题，本文提出一种自适应扩展卡尔曼滤波器(Adaptive Extend Kalman Filter，AEKF)。该算法将改进的Sage-Husa次优无偏极大估值器［9］与扩展卡尔曼滤波器相结合，在计算过程中对未知噪声的统计特性进行实时估计和修正，并利用测量值来判断滤波是否发散，当滤波发散时通过引入自适应衰减因子来修正预测状态协方差矩阵，进而调整测量方程协方差矩阵和滤波增益矩阵，抑制由于干扰所引起的滤波发散，提高滤波器的精度［10］。

1 自适应滤波算法

1. 1 动力学模型与测量模型

双星环月编队飞行动力学方程和测量方程可表示为:

式中:Xk表示目标在k时刻系统的状态向量，包括参考卫星在惯性空间的位置速度矢量、伴随卫星在惯性空间的位置速度矢量、月球引力场常数和月球J2项摄动系数14个量;Zk为k时刻编队卫星和参考卫星相对位置矢量在惯性空间的测量值;fk－1(Xk－1)为状态转移函数;Hk为测量转移矩阵;假设动力学方程的噪声wk为期望值为零，方差为Q的高斯白噪声序列，测量噪声vk是期望值为零，在区间(－1，1)均匀分布的噪声序列，测量噪声特性不满足标准EKF的条件。

1. 2 EKF 滤波算法

由式(1)可得预测状态值和预测测量值分别为:

计算状态转移矩阵Φk/k－1为:

预测状态的协方差矩阵和滤波增益矩阵为［11－12］:

估计状态值和协方差矩阵更新为:

1. 3 AEKF 滤波算法

在传统的EKF算法中，系统噪声和测量噪声为白噪声，并且方差Q和R都是已知的，但是在实际情况中噪声不一定为白噪声，且统计特性Q和R未知，不准确的噪声统计特性会影响状态估计的精度和稳定性，甚至引起滤波发散。针对这一问题，Sage与Husa(1969)提出了对Q或R进行修正估计的方案，同时张常云等［13］在对 Sage－Husa的 AEKF的后续研究中证明了该算法不能同时修正Q与R，并分析了该法导致分散的原因。

本文提出了一种改进的AEKF算法，该方法在滤波过程中，利用改进的Sage-Husa估计器估计未知测量噪声的统计特性，通过已知的Q可以准确地估计出R，并对滤波发散情况进行判断和抑制，有效提高了滤波数值的抗干扰性，减小了状态估计误差。

由(1)式与(3)式可得:

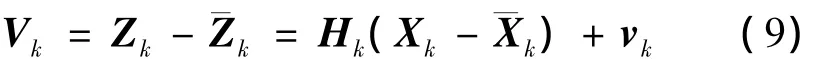
根据文献［14］，对(9)式两边同时取协方差可以得到预测误差向量的协方差矩阵:

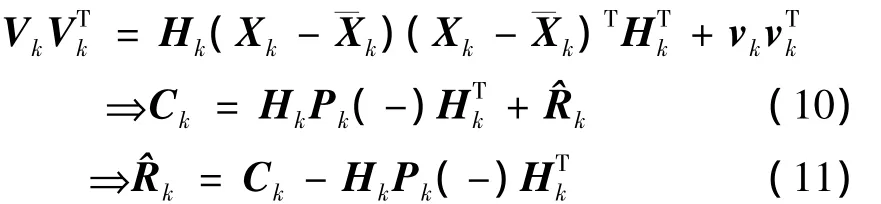
Ck的计算通常采用移动开窗估计法，则Ck的估计值可以为:

式中:N为窗口函数大小，从式(12)中可以看出，若N值过大，Ck不能反映观测噪声的瞬态特性，若N值选取过小，Ck易受当前预测残差向量的影响，导致估计值的平稳性较差。

1. 4 滤波发散的抑制

由于传统的EKF常常会出现发散的情况，本文提出一种基于协方差匹配判据的方法对滤波发散趋势进行判断，由

式中:tr(^Rk)表示矩阵 ^Rk求迹

若该式不成立，修正Pk(－)可得:

当满足式(13)的条件时，就采用前面所述Sage-Husa算法;而当不满足式(13)的条件时，就采用衰减因子计算公式［15－16］，得到一自适应加权系数 Ωk，再用它对Pk(－)进行修正，其中，Ωk由下式确定

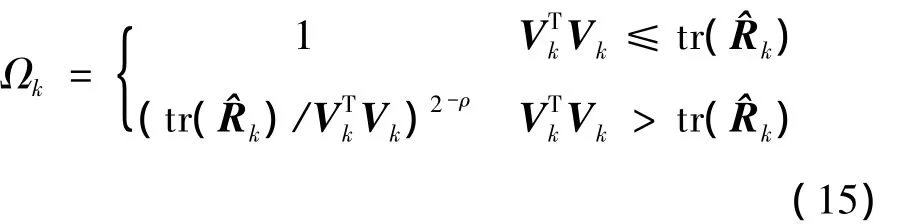
式中:ρ＞0为衰减系数，能进一步提高滤波器快速跟踪能力，通常取值在11左右，其值越小，则k时刻以前的信息所占的比例就越小，当前残差向量的影响就越突出，该方法有很强的关于突变状态的跟踪能力，并且在滤波达到稳定时，仍保持对于缓变以及突变状态的跟踪能力。

当采用自适应滤波算法时，由于算法实时对测量数据的方差R进行估计，并且将方差R应用到EKF增益式(6)的计算中。这样当测量数据误差较大时，EKF增益的值就会降低，测量数据在状态估计中的权重降低，导致状态估计精度降低速度减慢，提高算法的收敛性。

1. 5 AEKF滤波算法实现

针对式(1)描述的自主月球引力场确定问题，AEKF具体步骤如下(如图1):

1)状态初始条件为

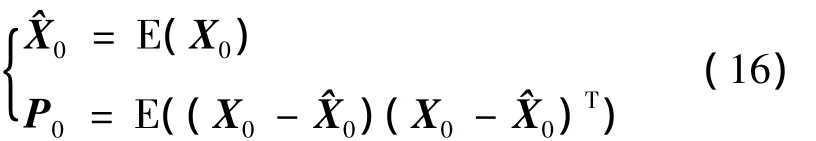
2)预测更新，对于给定的 Qk－1，Pk－1，根据式(2－4)，求状态预测，测量预测和预测协方差。

3)由式(11－12)估计测量噪声统计特性。

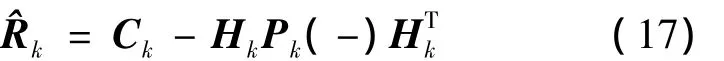
4)判断是否符合式(13)的条件，如不符合按照式(14－15)修正Pk(－)，符合就不需要修正Pk(－)直接进入下一步。

5)测量更新，根据式(6－8)得到量测更新和状态估计值。

2 仿真校验

为了校验本文AEKF的效果，在测量噪声统计特性未知的情况下，分别采用标准的EKF算法和AEKF算法进行仿真，并且与蒙特卡洛仿真(Monte Carlo Algorithm，MCL)的结果进行比较。

2. 1 坐标系的选取

根据文献［17］，建立本文所采用的坐标系:以OE－XEYEZE表示J2000地球惯性坐标系，原点为地心，基本面为地球平赤道面，XE轴指向历元J2000春分点，ZE轴指向地球北极，根据右手螺旋定律由XE轴和ZE轴确定YE轴方向，然后以月心为原点，将J2000地球惯性坐标系平移至月心，得到月心J2000惯性坐标系OL－XYZ;以OS-X'Y'Z'表示轨道坐标系，以参考卫星的质心为坐标原点，X'轴由月心指向参考卫星的质心，Z'轴指向参考卫星轨道面法向方向，Y'轴由右手法则，垂直于X'轴和Z'轴所组成的平面。本文用 XR，YR，ZR和 XF，YF，ZF分别表示参考卫星和伴随卫星在OL－XYZ坐标系中的三个方向矢量。

2. 2 仿真场景

本文基于Matlab7.0软件，在配置为因特尔奔腾的处理器(双核2.8 GHz)与两根海力士DDR3内存(2 GB)的计算机上对近月轨道飞行卫星编队进行仿真，考虑到月球 J2项摄动的影响，以月球LP165P模型为参考对象，通过AEKF算法实现伴随卫星和参考卫星在OL－XYZ坐标系中精确定轨，同时估计月球引力场常数和J2项摄动常数。本文仿真采用的伴随卫星和参考卫星的具体初始轨道根数如表1，2所示:

表1 参考卫星初始轨道根数Table 1 Initial orbit elements of reference satellite

表2 伴随卫星初始轨道根数Table 2 Initial orbit elements of follow satellite

根据文献［18］，假设系统状态方程噪声协方差矩阵 Qn=diag(1 × 10－6，1 × 10－6，1 × 10－6，1 ×10－10，1 × 10－10，1 × 10－10，1 × 10－6，1 × 10－6，1 ×10－6，1 × 10－10，1 × 10－10，1 × 10－10，1 × 104，1 ×10－36)。将表1中的初始轨道根数转化成OL－XYZ坐标系中的位置速度和LP165P中的月球引力常数与J2摄动常数，分别由式(1)得到参考卫星和伴随卫星在OL－XYZ坐标系中的绝对位置和速度，然后根据式(1)，得到编队卫星相对位置的测量值。

2. 3 仿真结果

分别对AEKF(衰减系数ρ=11窗口函数N=14)、先验噪声为 Rn=diag(1/3，1/3，1/3)的不同初始状态值的50组传统EKF和MCL仿真结果进行比较。

AEKF采用的初始状态误差为 ΔX=［9.76×102，7.56 ×102，9.03 × 102，9.82 × 10－1，1.02，8.95×10－1，9.48 × 102，1.05 × 103，1.06 × 103，1.06，8.51 ×10－1，8.92 ×10－1，5.09 ×108，8.71 ×10－7］，初始协方差矩阵都为 P0=diag(9.53×105，5.71×105，8.15 ×105，9.64 ×10－1，1.04，8.01 ×10－1，8.98×105，1.11 × 106，1.12 × 106，7.24 × 10－1，7.95 ×10－1，9.93 ×10－1，2.59 ×1017，7.59 ×10－13)。50 组传统EKF参考卫星三个方向的初始位置估计误差分布符合期望值是0，方差分别是9.53×105，5.71×105，8.15×105的高斯分布，三个方向的初始速度估计误差分布符合期望值是0，方差分别是9.64×10－1，1.04，8.01 ×10－1的高斯分布;伴随卫星三个方向的初始位置估计误差分布符合期望值是0，方差分别是 8.98 ×105，1.11 ×106，1.12 ×106的高斯分布，三个方向的初始速度估计误差分布符合期望值是 0，方差分别是 7.24 × 10－1，7.95 × 10－1，9.93×10－1的高斯分布;月球引力常数初始估计误差分布符合期望值是0，方差是2.59×1017的高斯分布，J2项摄动力常数初始估计误差分布符合期望值是0，方差是 7.59×10－13的高斯分布;50 组 Monte Carlo仿真的初始状态误差估计分布与传统EKF初始状态估计误差分布一样。

通过对环月编队卫星飞行7430 s的相对测量数据进行处理(测量更新间隔为5 s)，表3～5给出了三种方法估计最终时刻编队卫星位置速度，月球引力常数与J2项摄动力常数估计的一倍标准差。

表3 位置标准差比较Table 3 The standard deviation comparison of position in three-directions

表4 速度标准差比较Table 4 The standard deviation comparison of velocity in three-directions

表5 月球引力常数与J2项摄动力常数标准差比较Table 5 The standard deviation comparison of the lunar gravitational constant and the coefficient of the J2 perturbation

由表3～5可以看出:AEKF算法是收敛的，并且能有效地提高编队卫星轨道确定的精度。在7430 s的时间内，将初始X轴方向的位置误差的标准差从976 m(1σ)提高到 51.1 m(1σ)，并且使球引力常数精度和月球J2项摄动系数精度分别达到了4.43 ×108m3/s2(1σ)和 9.12 ×10－8(1σ);MCL仿真与AEKF算法得到的结果基本一致，校验了AEKF方法的正确性和有效性;传统EKF是发散的，说明与传统EKF假设不符合的测量噪声使得EKF不能有效地收敛，而AEKF算法由于对测量噪声的统计特性进行了实时修正，因此有效减少干扰影响，抑制发散从而提高了参数估计精度;EKF与AEKF方法运行一次的计算时间分别为 206.45 s和211.06 s，AEKF运行一次的时间较长，这是由于AEKF算法利用滤波器残差对测量噪声的统计特性进行了自动修正，增大了计算量从而增加了计算时间;该方法得到的月球引力常数精度为4.902801056 ×1012±4.43×108m3/s2(1σ)，归一化的J2项摄动常数为 －9.08 ×10－5±9.12 ×10－8(1σ)，虽然与 Alex S.Konopliv 等［1－3］人的结果相比得到的引力场模型精度较低，但是由于不需要例如深空探测网(美国GRAIL计划)，中继卫星(日本SELENE计划)等其他设施的辅助，能自主确定月球引力场，因此大大降低了任务实施的成本。

图2 均匀分布噪声下的EKF算法位置估计误差Fig.2 The estimation position error using EKF under uniformly distributed random measurement noisy

图3 高斯分布噪声下的EKF算法位置估计误差Fig.3 The estimation position error using EKF under gaussian distributed random measurement noisy

对传统EKF进一步分析，图2是在测量噪声是均匀分布噪声，同时改变编队卫星的初始估计误差(50组)情况下，采用EKF算法时参考卫星在OLXYZ坐标系下X轴方向的位置估计误差的曲线图;图3是在测量噪声是高斯分布噪声，同时改变编队卫星的初始估计误差(50组)情况下，采用EKF算法时参考卫星在OL－XYZ坐标系下X轴方向的位置估计误差的曲线图。比较图2与图3，可以看出，与EKF假设相同的测量噪声(高斯白噪声)，并且噪声统计特性准确知道的情况下，传统EKF运行的很好，结果可以快速收敛，但当测量噪声与传统EKF假设不相同时(非高斯白噪声)，传统EKF滤波精度不高，甚至引起滤波发散。

图4是在测量噪声是均匀分布噪声，同时改变编队卫星的初始估计误差(50组)情况下，采用AEKF算法时参考卫星在OL－XYZ坐标系下X轴方向的位置估计误差的曲线图。比较图2与图4可以看出:噪声不是高斯白噪声时，传统EKF算法的状态估计误差比AEKF算法的状态估计误差大，甚至引起滤波发散。这是因为传统EKF在滤波过程中一般假设测量噪声是高斯白噪声，但实际中测量噪声不一定是高斯白噪声;AEKF算法中测量噪声的统计特性会随着滤波器残差的大小自动修正，因此估计的精度和抗干扰性比较好。

3 结论

针对系统噪声或者测量噪声未知情况下月球的引力场确定问题，提出了一种新的基于残差信息调整方差的自适应EKF算法，该算法基于编队卫星相对位置测量能自主确定月球的引力场，同时能对可能出现的滤波算法发散情况进行抑制，减少外界干扰对月球引力场测量的影响。文中给出的仿真实例校验了该方法的有效性，仿真结果表明本文提出的AEKF算法滤波效果要明显优于传统EKF算法，精度高，抗干扰性强，月球引力常数和月球J2项摄动常数测量精度分别达到了4.43×108m3/s2(1σ)和9.12 ×10－8(1σ)。

［1］ Konopliv A S，Park R S，Yuan D N，et al.The JPL lunar gravity field to spherical harmonic degree 660 from the GRAIL primary mission［J］.Journal of Geophysical Research，2013，118:1415－1434.

［2］ Matsumoto K，Hanada H，Namiki N，et al.A simulation study for anticipated accuracy of lunar gravity field model by Selene tracking data［J］.Advances in Space Research，2008，42(8):331－336.

［3］ Goossens S，Matsumoto K，Liu Q，et al.Lunar gravity field determination using SELENE same-beam differential VLBI tracking data［J］.Journal of Geodesy，2011，85(4):205 －228.

［4］ Yan J G，Baur O，Fei L，et al.Long-wavelength lunar gravity field recovery from simulated orbit and inter-satellite tracking data［J］.Advances in Space Research，2013，52(11):1919 －1928.

［5］ Tanaka S，Shiraishi H，Kato M，et al.The science objectives of the SELENE-Ⅱ mission as the post SELENE mission［J］.Advances in Space Research，2008，42(2):394－401.

［6］ Mark L P.Absolute orbit and gravity determination using relative position measurements between two satellites［J］.Journal of Guidance，Control，and Dynamics，2011，34(5):1285 －1297.

［7］ 尚琳，刘国华，张锐，等.基于BP神经网络的自主定轨自适应Kalman滤波算法［J］.宇航学报，2013，34(7):926－931.［Shang Lin，Liu Guo-hua，Zhang Rui，et al.An adaptive Kalman filtering algorithm for autonomous orbit determination based-on BP neural network［J］.Journal of Astronautics，2013，34(7):926 －931.］

［8］ 席燕辉，叶志成，彭辉.一种基于自适应粒子滤波的多层感知器学习算法［J］.中南大学学报(自然科学版)，2013，44(4):1397 －1402.［Xi Yan-hui，Ye Zhi-cheng，Peng Hui.An algorithm for MLPs training based on adaptive particle filter［J］.Journal of Central South University(Science and Technology)，2013，44(4):1397 －1402.］

［9］ Sage A P，Husa G W.Adaptive filtering with unknown prior statistics［C］.Joint Automatic Control Conference，Boulder Colorado，USA，August，1969.

［10］ 石勇，韩崇昭.自适应UKF算法在目标跟踪中的应用［J］.自动化学报，2011，37(6):755－759.［Shi Yong，Han Chong-zhao.Adaptive UKF method with applications to target tracking［J］.Acta Automatica Sinica，2011，37(6):755 －759.］

［11］ 陈宇波，宋迎春.非高斯噪声下的车载GPS信号定位算法［J］.中南大学学报(自然科学版)，2010，41(4):1462－1466.［Chen Yu-bo，Song Ying-chun.A Bayes filter algorithm with non-Gaussian noises based on location of vehicular GPS［J］.Journal of Central South University(Science and Technology)，2010，41(4):1462 －1466.］

［12］ 傅荟璇，王宇超，孙枫.融合Kalman滤波的自适应带宽Mean Shift算法［J］.中南大学学报(自然科学版)，2011，42(1):784 － 788.［Fu Hui-xuan，Wang Yu-chao，Sun Feng.Tracking algorithm based on Kalman and mean shift with adaptive bandwidth［J］.Journal of Central South University(Science and Technology)，2011，42(1):784 －788.］

［13］ 张常云.自适应滤波方法研究［J］.航空学报，1998，19(7):96－99.［Zhang Chang-yun.Approach to adaptive filtering algorithm［J］.Acta Aeronautica et Astronautica Sinica，1998，19(7):96 －99.］

［14］ 王志忠，朱建军.非线性模型中方差和协方差分量的估计［J］.测绘学报，2005，34(4):288－293.［Wang Zhi-zhong，Zhu Jian-jun.Estimation of variance and covariance components in the nonlinear model［J］.Acta Geodaetica et Cartographica Sinica，2005，34(4):288 －293.］

［15］ Yang Y X，Gao W G.An optimal adaptive Kalman filter［J］.Journal of Geodesy，2006，80(4):177－183.

［16］ Hide C，Moore T，Smith M.Adaptive Kalman filtering for lowcost INS/GPS［J］.The Journal of Navigation，2003，56(1):143－152.

［17］ 李立涛，杨涤，崔祜涛.奔月轨道的一种求解方法［J］.宇航学报，2003，24(2):150－155.［Li Li-tao，Yang Di，Cui Hutao.One method of calculating cislunar transfer trajecotry［J］.Journal of Astronautics，2003，24(2):150 －155.］

［18］ 张艳.基于星间观测的星座自主导航方法研究［D］.长沙:国防科学技术大学，2005.［Zhang Yan.Study on autonomous navigation of constellation using inter-satellite measurement［D］.Changsha:National University of Defense Technology，2005.］