利用改进TW-API方法在轨辨识挠性航天器时变模态参数
倪智宇,邬树楠,,吴志刚,,谭述君
(1.大连理工大学工业装备结构分析国家重点实验室,大连116024;2.大连理工大学航空航天学院,大连116024)
0 引言
航天工程中许多问题需要考虑系统的时变特性,例如大型空间结构装配、太阳能帆板展开与旋转等,这些动态过程造成系统模态参数发生改变。随着航天技术的进展,大型化与挠性化成为航天器结构的一个重要发展趋势。航天器挠性化导致固有频率值很低,刚柔耦合现象明显。对于大型刚柔耦合空间结构,通过有限元数值计算和地面动力学试验辨识得到的参数必然存在着一定的误差,甚至由于结构过大过于复杂而无法进行地面试验。对于具有时变动力学特性的大型航天器,利用在轨飞行中的输入输出测量数据,采用在轨辨识算法获取航天器模态参数随时间的变化特性具有重要意义。
在航天器在轨辨识试验中,往往利用飞轮或姿控推力器产生激励信号,通过测量得到的姿态角和角速度,以及星体姿态运动和大型附件振动的耦合关系来进行航天器动力学参数辨识。为更精确地测量航天器的动态响应,选择在太阳能帆板上布设传感器来获得加速度信号用于参数辨识。但是如何产生有效的输入信号以保证安全而有效地激发航天器的固有模态特性,以及如何在帆板上合理布置传感器以获得所需的输出信号(实际在轨辨识中,传感器数目有限),即作动器的激振和传感器配置优化问题[1],这些都是航天器在轨参数辨识研究中的重要课题和难点,需要进一步研究。在实际的航天器在轨辨识试验中,Juang等采用ERA系列方法[2],使用控制力矩输入信号和陀螺仪量测信号数据,对哈勃太空望远镜进行了系统频率、阻尼等模态参数的在轨辨识。文献[3]利用星上助推火箭产生的随机激励信号,测量帆板的加速度信号和星体的姿态信号,对ETS-VI卫星进行了系统的在轨辨识试验和鲁棒控制试验。而Kasai等[4]对ETS-VIII卫星的在轨模态参数进行了一系列的辨识试验。
在航天器模态参数辨识中,子空间系列方法得到了广泛发展和应用[5]。在各类子空间方法中,基于信号处理技术提出的递推子空间方法由于具有较快的计算速度,在航天器动力学参数辨识方面具有一定优势。Yang[6]根据信号子空间投影原理,提出了投影估计子空间跟踪(Projection Approximation Subspace Tracking,PAST)方法。庞世伟等[7]利用该方法辨识了移动质量-简支梁的时变模态参数。Badeau等[8]针对PAST方法信号子空间列向量不能严格正交的问题,提出了逼近幂迭代(Approximation Power Iteration,API)方法,对信号子空间投影乘以修正后的正交矩阵,使其投影子空间保持严格正交的同时可以跟踪快变的主子空间。与利用整体数据的子空间辨识方法相比,递推辨识方法不需要逐一时刻进行SVD分解计算,而是通过信号子空间迭代以避免较高维数的Hankel矩阵求解问题,从而减小了计算量。
传统截断窗逼近幂迭代(Truncated Window-Approximation Power Iteration,TW-API)递推方法的计算量可以达到O(n3),其中n为系统的阶次。对于航天器在轨辨识而言,过长的计算时间必然会影响辨识效率。而本文简化了数据递推步骤中的计算,使得这种方法的计算量大幅减少,改进后算法的总计算量只有 O(n2),本文还对另外两种经典PAST和API递推方法的计算量进行了总结。为对比这几种经典递推方法在航天器在轨辨识中的计算速度和计算精度,选取ETS-VIII卫星作为数值仿真对象,辨识太阳能帆板转动所造成的整星模态参数时变特性。结果表明本文提出的改进TW-API方法与现有大多数方法相比,在计算时间上具有一定的优势,对于航天器在轨辨识有一定的实用价值。
1 航天器建模与输入/输出数据的前处理
1. 1 航天器约束模态姿态模型
常见的航天结构如卫星和空间站等,往往将其作为刚柔耦合结构来建模。基于航天器刚体转动方程和挠性附件振动方程,并且在刚柔耦合系数中只考虑附件振动对刚体转动的影响,建立约束模态刚柔耦合动力学方程[9]:

式中:θ为附件绕自身纵向中心轴旋转的旋转角;fm为航天器反作用飞轮产生的控制力矩。Ψ和J(θ)分别为整体结构的姿态角矢量和转动惯量;Pj(θ)为第j个附件振动和中心刚体转动耦合的挠性系数耦合矩阵;μj为第j个挠性附件的模态坐标;Ω2j为中ωjp为挠性附件j的第p阶模态频率;ζj为对应的附件j的阻尼比。
将动力学方程(1)和(2)改写为如下形式:

其中,矩阵M、E和K的详细形式见文献[10]。方程中的状态量q和系数矩阵L分别为

式中:矩阵L中的零矩阵维数为3pN,p为上文中提到的每个附件所选取的模态阶数,而N为航天器结构中所包含的附件数目。
从方程(1)和(2)可以看出,所构建的动力学方程(3)里包含有结构刚体运动和弹性振动两部分。姿态控制力矩通过刚柔耦合系数矩阵对系统振动方程产生影响。因此本文利用飞轮产生的力矩作为激励信号,系统的姿态角、姿态角速度以及帆板上的传感器测得的附件振动响应作为输出信号进行时变系统模态参数的辨识。利用飞轮力矩作为输入信号的优点是可以使用卫星正常运行的数据来进行辨识试验。例如ETS-VIII卫星的在轨辨识试验就将稳态运行阶段的姿态机动信号作为辨识的输入信号,从而有利于卫星姿态保持,避免额外的燃料消耗。需要说明的是,本文只选用了飞轮的控制力矩作为输入信号,暂未考虑其它激励条件如热致振动或冲击输入的影响。
本文在考虑附件旋转角速度ωθ为常值的情况下,建立附件旋转角θ和时间t之间的线性对应关系θ=ωθt,从而将方程(3)中的线性变参数模型转化为线性时变模型进行分析。
1. 2 航天器输入/输出信号的前处理
为利用子空间跟踪算法进行航天器模态参数在轨辨识,输入输出数据的前处理必不可少,PAST和API等递推方法均需要通过系统输入/输出数据矩阵,构建对应时刻子空间跟踪中的输入信号状态量,然后在子空间追踪方法中不断更新该状态量,达到对系统的能观性矩阵(即信号子空间)的追踪求解,从而辨识时变系统的模态参数。
首先考虑将方程(3)改写为如下离散状态方程形式
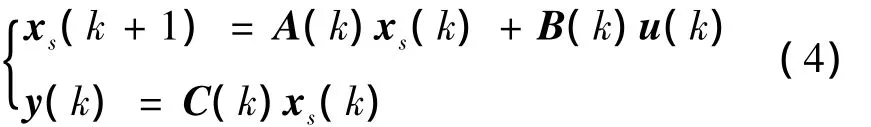
式中:系统阶数为n,输入维数为r,输出维数为m。任意k时刻的输入矩阵U(k)和输出矩阵Y(k)以及下一时刻输入数据¯u(k+1)和输出数据¯y(k+1)的Hankel矩阵形式分别写为

式中:

其中,M为合适的Hankel矩阵维数。根据数据更新的 URV 递归方法[11],令

则通过输入输出数据生成的状态量z(k)的更新方式为
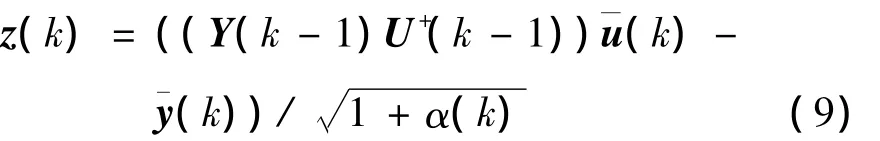
式中:“+”表示伪逆。在式(7)和(9)中,下一个时刻k的(U(k)UT(k))-1和Y(k)U+(k)的更新方式为

通过式(7)~(11)的递推,利用各个时刻的¯u(k)和¯y(k)构建出每个时刻的状态量z(k)(即在信号子空间中的每个时刻的输入信号),以满足子空间迭代求解中的数据更新条件。
2 用于参数辨识的两种经典子空间递推方法
2. 1 PAST 方法
Yang基于信号子空间原理提出了PAST方法[6]。PAST方法总计算量为3mMn+O(n2),计算量较小,这在航天工程中是比较适用的。但是该方法不能保证所得到的子空间列向量完全投影正交,所以PAST方法对于辨识快变系统的参数存在不足。为解决这种问题,文献[8]提出API系列方法。
2. 2 API方法
相比较PAST方法,API方法(基于无限指数窗)在子空间递推方面增加了正交项,以保证投影矩阵的正交性,同时还加强了对快变子空间的跟踪性能,因此对于时变程度较快的系统仍能较好地跟踪和辨识[8]。
API方法计算量为mM(n2+3n+1)+O(n3),高于PAST方法,但是系统的正交性和对快变子空间的跟踪性能更好。无论是PAST还是API方法,均是基于无限指数窗形式,对于系统信号发生突变的情况不能够很好跟踪,为此又在原有方法的基础上,提出了基于滑移窗的截断窗逼近幂迭代递推方法(TW-API)。
3 改进的TW-API方法
本文只给出针对传统TW-API方法所进行的改进,该方法的具体推导过程见文献[8]。传统TWAPI方法计算量为6mMn+mMn2+n2l+O(n3),其中l为选取的截断窗的长度,可看出计算量明显高于指数窗形式的API方法。在原TW-API方法中,复迭代的步骤。另外,传统TW-API算法中,在更新矩阵Z(k)和正交矩阵Θ(k)这两步骤中的计算量均为O(n3),由于航天器系统的阶次往往普遍较高,这对方法整体的计算量将会有极大的影响。为此,本文考虑减少原TW-API方法中有关矩阵Z(k)和Θ(k)的递推计算量(Z(k)和Θ(k)的原表达式见文献[8]的表2)。
首先从子空间输出信号 s-(k)的自相关函数Css(k)的递推关系出发,因为Z(k)=(k),而自相关函数的递推关系为

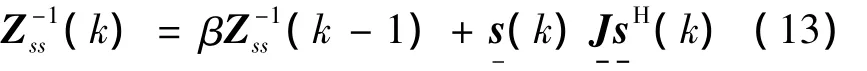
根据矩阵求逆引理,对于B=A+PJQ,存在有

那么利用式(14)的求逆引理对式(13)进行求逆,并定义一个临时变量h(k)(h(k)的具体形式见表1)可以得到

原TW-API方法中Z(k)的计算量为3n2+4n3,而式(15)给出的Z(k)新的递推步骤的计算量为20+10n+5n2,从阶次上可以看出明显地减少了计算量。
接下来考虑Θ(k)的递推步骤的改进,定义ε-(k)为文献[8]里原误差矩阵 e-H(t)e-(t)的平方根
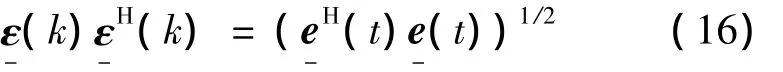
则有
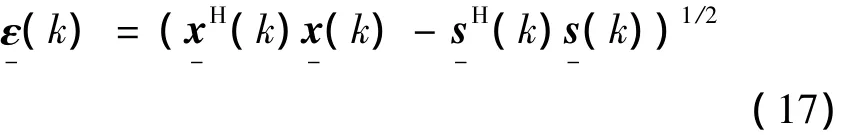
利用文献[8]中Θ(k)的表达式,可以得到

式中:In为单位矩阵,g(k)的具体形式见表1,将式(16)代入式(18)并应用矩阵求逆引理,可得

其中,ρ-(k)为2×2的正定矩阵:

考虑式(19),寻找一个特解σ-(k)使其满足:

那么特解 σ-(k)= ρ-(k)+(ρ-H(k))1/2。
定义2×2的正定矩阵τ-(k)为

则

这样就得到了Θ(k)的新的递推关系。原TW-API方法计算Θ(k)的计算量为4mM+O(n3),而新方法中Θ(k)递推步骤的总计算量为O(n2),同样简化了计算量。改进后的TW-API方法的计算量为mM(n2+6n+4)+O(n2),改进后的TW-API方法的递推步骤见表1,其中递推计算中的初始条件选为W(0)=过程中,由第1.2节中生成的各个时刻的z(k)作为各个时刻的输入值x(k)。表2则给出了以上提到的四种子空间递推方法的计算量和适用范围的总结。

表1 改进后的TW-API方法递推步骤Table 1 The recursive step of the improved TW-API method

表2 四种方法的复杂性的比较Table 2 Comparison of the four algorithms'complexities
利用子空间递推方法计算得到各时刻的信号子空间W(k)后,离散的系统矩阵A^(k)可以通过下式得到

式中:W1(k)和 W2(k)分别为矩阵 W(k)的前(M-1)×m行和后(M-1)×m行元素所组成的矩阵。矩阵上标“^”表示辨识值。
根据时变系统的伪模态理论,即认为在很小的采样时间内,系统的特征根是不变的,对应于该时刻的特征根称其为“伪”特征根,将这种利用定常系统的理论来描述得到时变系统模态参数的方法称为“伪”模态分析方法。从航天工程的角度来说,只要采样间隔足够小,那么伪特征根对于系统的时变情况的反映是近似而合理的。
对辨识得到的A^(k)矩阵进行特征值分解可得

式中:Λ(k)=diag(λ1(k),…,λn(k))为对角特征根矩阵,ψ(k)为时变特征向量,λi(k)是时变共轭复特征根。第i阶伪特征根λi(k)=exp(-ζi(k)Δt± iωdi(k)Δt),ζi(k)为系统第 i阶伪阻尼比,ωdi(k)为系统的第i阶含阻尼的伪固有频率,Δt为采样时间。
4 数值实例
4. 1 卫星模型的建立与简化
本文在数值算例中,以日本的ETS-VIII卫星为研究对象,它的基本构型以卫星本体为中心,一对太阳能帆板(以下简称帆板n和s)以及一对巨大的抛物面通讯天线(以下简称天线a和b)通过硬质连杆铰接到卫星本体上[10]。利用前文提到的基于约束模态模型的航天器刚柔耦合动力学方程,建立该卫星的状态空间方程。
本文在对卫星进行有限元建模时将天线的壳型薄板简化为矩形平板,且天线和帆板处在同一平面上,该平面经过卫星本体的质心;卫星本体简化为长方体,而附件坐标系均建立在各自的质心上,总体坐标系的原点取在整星的质心上。简化后的卫星结构如图1所示。
由于ETS-VIII为地球同步卫星,帆板在电机的驱动下绕卫星的俯仰轴进行转动以保证始终朝向太阳以获得足够的电力,其旋转角θ是周期变化的,从而导致卫星的模态参数是时变的,令帆板旋转角速度为0.6(°)/s。该系统中前三阶为刚体运动对应的模态参数,从第四阶开始对应弹性振动。
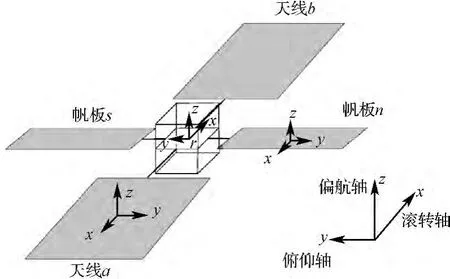
图1 简化后的卫星示意图Fig.1 Simplified image of satellite
4. 2 仿真辨识结果
选取采样时间为Δt=0.1 s,进行10次随机试验,Hankel矩阵中M=20,仿真时在输出中加入2%的量测白噪声干扰。分别利用改进TW-API、传统TW-API、PAST和指数窗API四种辨识方法进行卫星系统振动模态频率的辨识。关于截断窗长度l的选取,通常情况下令0.5mM ≤ l≤2mM[8],其中mM即为矩阵W(k)的行数,窗的长度太小的话将直接影响计算的精度。在本文中l的长度取为l=1.5mM。这里均以系统第4阶频率值的辨识结果为例,辨识结果如图2~图5所示。

图2 改进TW-API方法的频率辨识结果Fig.2 Identification results of frequencies by the improved TW-API method

图3 传统TW-API方法的频率辨识结果Fig.3 Identification results of frequencies by the traditional TW-API method

图4 PAST方法的频率辨识结果Fig.4 Identification results of frequencies by the PAST method

图5 API方法的频率辨识结果Fig.5 Identification results of frequencies by the API method
从图2~图5可以看出,这几种方法均能很好地辨识卫星的模态参数。接下来从计算时间上将四种方法进行比较,为此分别进行10次蒙特卡罗试验,其中统计采样点数为10,000个,计算所需要的仿真时间。仿真的系统硬件条件为:Windows 8 64位系统、CPU处理器Intel酷睿i7 4700MQ、内存容量8G,数值仿真使用的软件为Matlab,各辨识方法在计算机仿真中所需要的平均计算时间见表3。

表3 四种递推方法的计算时间Table 3 The computation time of the four recursive methods
从表3可以看出,四种方法所需要的计算时间:PAST<改进TW-API<API<传统TW-API。这与之前计算量分析的结论相吻合。与传统的TW-API方法相比,改进后的TW-API方法可以提高近50%的计算效率,虽然在计算时间上仍高于PAST方法,但是低于指数窗形式的API方法,证明该方法有效简化了计算量。
为定量比较这几种递推方法在航天器辨识中的计算精度,定义辨识结果的平均绝对百分误差(Mean Absolute Percentage Error,MAPE)如下
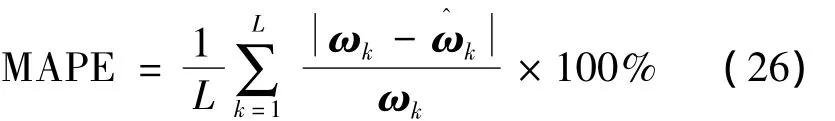
从表4可以看出,本文提出的改进TW-API方法由于采用截断窗形式,所以与采用指数窗形式的PAST和API方法相比,误差稍有增加,但误差的精度量级仍能很好地满足辨识要求。综合分析表3和表4给出的数据结果,可以看出改进的TW-API方法在保证计算精度的前提下,大幅减少了递推过程中所需的计算量,证明本文提出的方法在航天器系统的模态参数辨识方面是有效的。

表4 频率的MAPE的比较Table 4 Comparison of the frequencies'MAPE
在数值仿真中,如果令卫星的帆板转速增加为6(°)/s,即令系统成为一个快速变化的系统,比较这几种方法对于快变系统的辨识效果。图6给出了第四阶频率前60 s的辨识结果,从图中可以看出,当时变系统变化较快时,API/TW-API系列方法比较准确地跟踪了系统的频率值,而PAST方法对于快变系统的跟踪性能有所下降。特别是在曲线的拐点处,该方法得到的频率值与API/TW-API方法相比,存在着比较大的误差。

图6 四种方法的频率辨识结果Fig.6 Identification result of frequency by the four methods
在该算例的最后,我们考虑在航天器时变模态参数在轨辨识时,飞轮实际施加的力矩输入信号值与理论值存在误差的情况。在实际工程应用中,飞轮通过控制转速来得到相应的力矩,但是由于飞轮容易存在输出扰振的情况,从而导致获得的实际输入信号值与想要的力矩值存在一定的计算误差。这里将这种误差作为干扰信号加入到原输入信号中,分别考虑具有如下两种输入噪声干扰的情况:1)原方波输入信号u(k)中含有1%白噪声干扰;2)方波输入信号u(k)中含有大小为0.1×u(k)的测量误差。

图7 输入信号含有1%白噪声干扰时的第四阶频率结果Fig.7 The result of the fourth-order frequency with the 1%white noise in the input signal
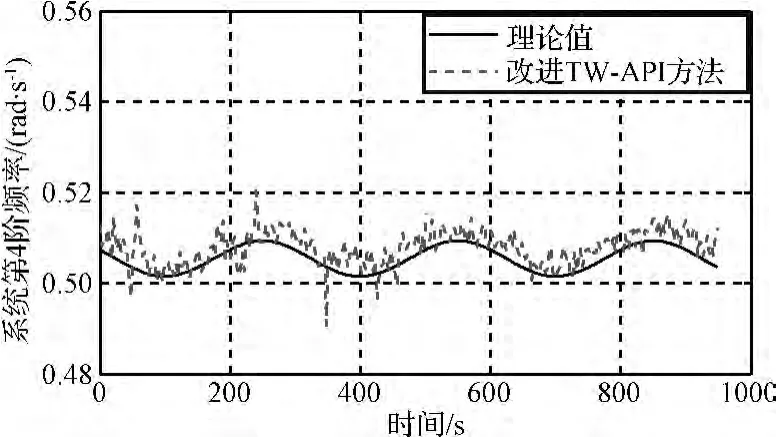
图8 输入信号含有0.1×u(k)噪声干扰时第四阶频率结果Fig.8 The result of the fourth-order frequency with the noise 0.1 × u(k)in the input signal
在这两种情况下利用本文的改进TW-API方法对航天器时变模态参数(以系统第4阶频率为例)的辨识结果如图7~图8所示。从图7~图8中的结果可以看出,当输入信号存在一定的白噪声干扰或是测量上的误差时,挠性航天器的时变模态参数仍能够有效地得到辨识。
5 结论
对于大型航天器模态参数的在轨辨识,所选方法的计算量和计算速度是工程技术人员需要考虑的一个重点。本文提出的改进的TW-API方法,通过递推步骤的改进,大大提高了这种递推方法的计算效率。同时还将改进的TW-API方法与传统的TWAPI方法以及经典的PAST和API递推方法进行了计算效率的比较,详细分析了这四种方法的计算效率和适用条件,结果证明本文提出的方法与其他三种方法相比,具有很好的辨识计算速度和精度,数值仿真结果也证明了这一点。
[1] 徐敏强,宋其江,王日新.基于可观测性和可靠性的传感器分布优化设计[J].宇航学报,2010,31(11):2618-2622.[Xu Min-qiang,Song Qi-jiang,Wang Ri-xin.Optimization design of sensors location based on fault observability and reliability[J].Journal of Astronautics,2010,31(11):2618 -2622.]
[2] Juang JN,Phan M,Horta L G,et al.Identification of observer/Kalman filter Markov parameters-theory and experiments[J].Journal of Guidance,Control,and Dynamics,1993,16(2):320-329.
[3] Adachi S,Yamaguchi I,Kida T,et al.On-orbit system identification experiments on engineering test satellite-VI[J].Control Engineering Practice,1999,7(7):831 -841.
[4] Kasai T,Yamaguchi I,Igawa H,et al.On-orbit system identification experiments of the engineering test satellite-VIII[J].Transactions of Space Technology Japan,2009,7(26):79-84.
[5] 孔宪仁,张红亮,张也弛.用于统计能量分析参数辨识的子空间方法研究[J].宇航学报,2011,32(12):2471-2477.[Kong Xian-ren,Zhang Hong-liang,Zhang Ye-chi.Study on subspace method applied to SEA parameter identification[J].Journal of Astronautics,2011,32(12):2471 -2477.]
[6] Yang B.Projection approximation subspace tracking[J].IEEE Transactions on Signal Processing,1995,43(1):95-107.
[7] 庞世伟,于开平,邹经湘.用于时变结构模态参数识别的投影估计递推子空间方法[J].工程力学,2005,22(5):115-119.[Pang Shi-wei,Yu Kai-ping,Zou Jing-xiang.A projection approximation recursive subspace method for identification of modal parameters of time-varying structures[J].Engineering Mechanics,2005,22(5):115 -119.]
[8] Badeau R,David B,Richard G.Fast approximated power iteration subspace tracking[J].IEEE Transactions on Signal Processing,2005,53(8):2931-2941.
[9] 史纪鑫,曲广吉.可变构型复合柔性结构航天器动力学建模研究[J].宇航学报,2007,28(1):130-135.[Shi Ji-xin,Qu Guang-ji.Mathematical modeling of a class of variable structure spacecraft with flexible multibody appendages[J].Journal of Astronautics,2007,28(1):130 -135.]
[10] Yoshiro H,Takashi O,Takashi K,et al.Synthesis of a linearly interpolated gain scheduling controller for large flexible spacecraft ETS-VIII[J].Control Engineering Practice,2011(19):611 -625.
[11] Tasker F,Bosse A, Fisher S. Real-time modal parameter estimation using subspace methods:theory[J].Mechanical Systems and Signal Processing,1998,12(6):797-808.

