主动隔振系统激励器电流分配优化设计
刘 伟,董文博,李宗峰,彭 超
(1.中国科学院空间应用工程与技术中心,北京100094;2.中国科学院空间科学与应用总体部,北京100094)
主动隔振系统激励器电流分配优化设计
刘 伟1,2,董文博1,2,李宗峰1,2,彭 超1,2
(1.中国科学院空间应用工程与技术中心,北京100094;2.中国科学院空间科学与应用总体部,北京100094)
主动隔振控制系统执行机构由八个输出单方向洛伦兹力的激励器构成,输出六自由度的力/力矩。针对八激励器输出力的分配优化问题,建立了力学模型和分配电流模型,并以总功耗最小为性能指标设计了拉格朗日乘子法,获得激励器分配电流解析解。当激励器分配电流超出电流边界时,进行二次优化,进一步提高执行机构输出零误差的能力。为保证控制系统对执行机构输出精度要求,分析了激励器各项误差允许范围。数值仿真结果表明,拉格朗日乘子法进行激励器电流优化分配的力可以达到系统要求,变化平稳,同时计算效率较高,具有一定的工程应用价值。
主动隔振;洛伦兹力激励器;电流分配;拉格朗日乘子法;二次优化
1 引言
良好的微重力水平是微重力科学实验成功的重要保障。然而载人航天器受到各种扰动力的影响,内部微重力水平并不理想,为此,美国、加拿大等早在上世纪八十年代初就已经开展主动隔振技术研究,研发了STABLE[1](Suppression of Transient Accelerations by Levitation)、MIM[2](Microgravity Vibration Isolation Mount)系列、ARIS[3](Active Rack Isolation System)和g-LIM-IT[4](GLovebox Integrated Microgravity Isolation Technology)等隔振装置,并在航天飞机和空间站上进行技术验证和实际应用,有效保证了微重力实验所需要的加速度水平。中国科学院空间应用工程与技术中心研发了一套空间高微重力主动隔振装置[5],着力于解决高微重力主动振动隔离技术问题,在航天器上实现10-4~10-6g量级的微重力环境,满足绝大多数空间科学实验的微重力需求。
主动隔振装置主体(见图1)分为定子、浮子和屏蔽外箱三部分。定子是装置的支撑单元,浮子是科学实验载荷的安装台。浮子和定子之间通过脐带线(主要是电缆线)相连,脐带线是定子传递给浮子扰动的唯一途径。为避免货船密封舱内空气扰动以及解决实验装置对货船平台的电磁辐射问题,需要对载荷和实验装置外围加装屏蔽外箱。
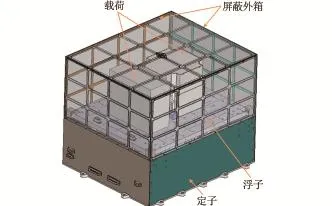
图1 主动隔振装置示意图Fig·1 The schem atic diagram of the active vibration isolation device
主动隔振控制系统执行机构由八个输出单一方向洛伦兹力的激励器构成。每个激励器由永磁铁和通电线圈组成,永磁铁固联于浮子上,通电线圈固联于定子上,如图2所示。
为提供六自由度控制力/力矩,八激励器可以采用两种工作方案。方案一:选择六个工作(其余两个备份),得到分配电流唯一解[6]。方案二:八个同时工作,采用约束优化算法,如拉格朗日乘子法[7]、序列二次规划[8]、粒子群算法[9]等,以八激励器总功耗最小为性能指标进行优化。比较两种方案,显然方案一是方案二的一个特例。方案二充分利用资源,输出能力和总功耗均优于方案一。本文选用方案二进行八激励器分配电流优化设计,采用拉格朗日乘子法,可以得到解析解,避免迭代计算过程,提高算法效率,适用于工程实际。当激励器分配电流超出电流边界时,进行拉格朗日乘子法二次优化,进一步提高执行机构输出零误差的能力。
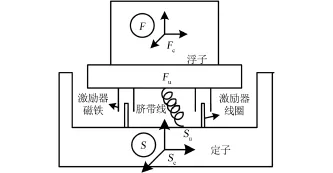
图2 主动隔振装置激励器结构示意图Fig·2 The schematic diagram of the actuator structure of the active vibration isolation device
2 激励器电流分配模型
首先建立各坐标系,如图2所示。定子形心坐标系○S,原点在定子形心Sc,固联于定子。浮子形心坐标系Ⓕ,原点在浮子形心Fc,固联于浮子。浮子质心坐标系ⓕ,原点在浮子质心F0,固联于浮子,且三轴方向与Ⓕ系三轴方向相同。
2.1 单激励器作用力模型
根据洛伦兹力原理,单个激励器作用力如式(1):

式中,I为线圈通电电流;L为线圈等效长度;B为线圈处等效磁通密度。式(1)计算得到的是磁场对通电线圈的作用力F,而激励器对浮子的作用力Fzd,即通电线圈对磁场的作用力,与F是一对作用力与反作用的关系,根据牛顿第三定律,F和Fzd大小相等,方向相反,作用在同一条直线上。
由于磁场分布不均匀,在磁场和线圈确定的条件下,激励器对浮子的作用力Fzd可以表示为式(2):

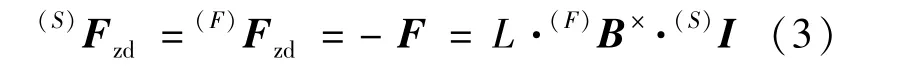
式中,B×表示矢量B的斜对称矩阵。
2.2 八激励器作用力和力矩模型
定义激励器固联坐标系,原点位于激励器安装点位置,x轴沿磁感强度正方向,y轴沿电流正方向,z轴满足右手坐标系法则。八个激励器分别编号为1~8,用下脚标m表示,如图3所示。
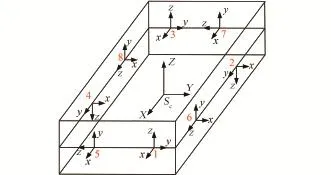
图3 八个激励器安装方式示意图Fig·3 The installation schematic diagram of eight actuators
已知m号激励器安装点在Ⓕ系中表示为(F)Rfm=RfmxRfmyRfmz
[ ]T,m号激励器电流

设浮子质心F0在ⓕ系中的坐标表示为(F)rFcF0,则激励器输出对浮子质心力矩的力臂在Ⓕ系中的表示为式(5):
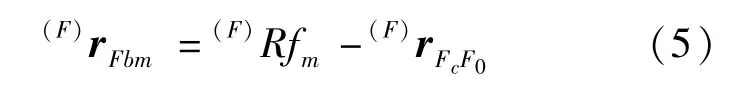
由控制器计算出控制指令力(S)Fc、指令力矩(F)Mc,则各激励器输出力满足式(6):
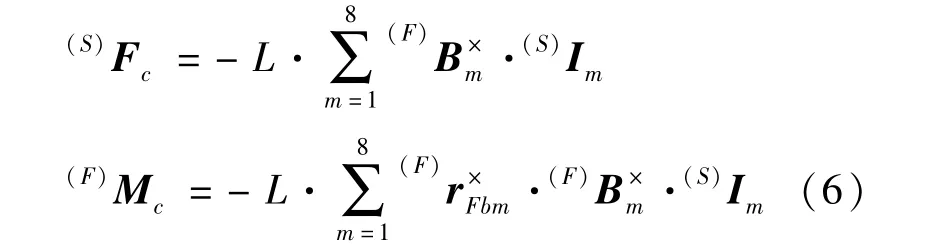
为简化表达,设式(7):

将式(4)、式(7)带入式(6),并整理可得八激励器作用力和力矩模型如式(8):
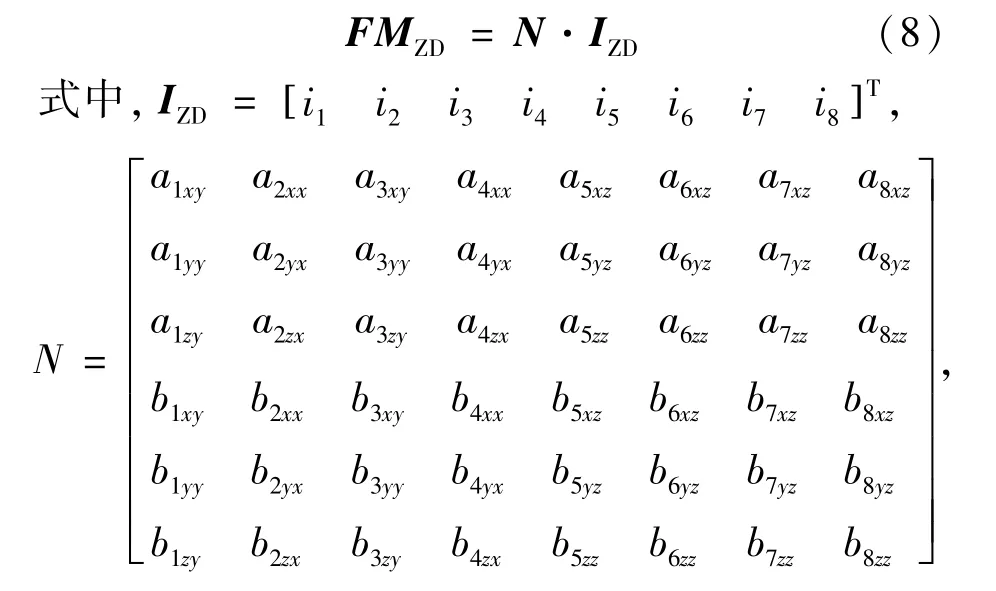
3 激励器分配电流优化设计
3.1 拉格朗日乘子法
考虑到功耗最小,取优化指标函数f(I)如式(9):


求一阶导数得到式(11)所示的方程组:

整理可得式(12):
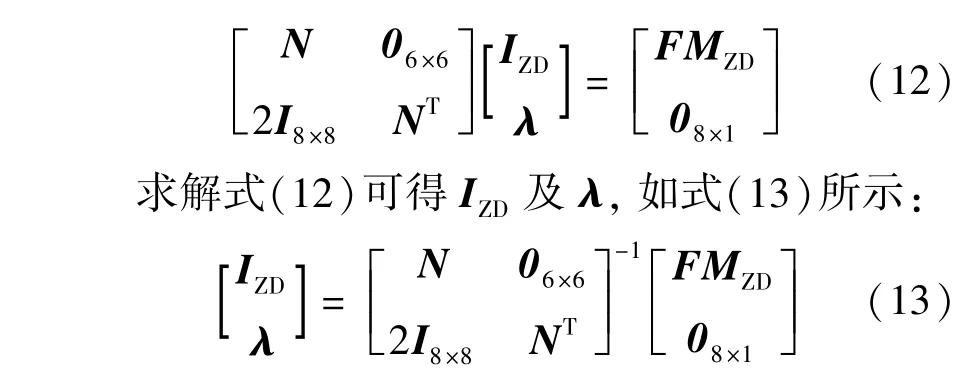
3.2 二次优化
当式(13)计算得到的分配电流中有电流超出电流边界值iborder时,根据式(14)重新赋值分配电流。

并将超出电流边界的电流下标号按顺序存储记录在矩阵K中,假设有p个电流超出电流边界,则有式(15):
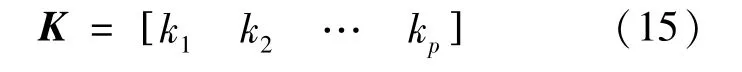
剩余8-p个电流按顺序存储记录在矩阵C中,即式(16):
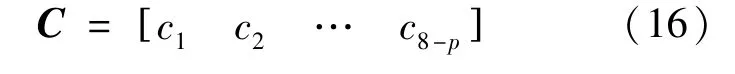
根据K和C将分配电流重新整理,如式(17)所示:

同时调整系数矩阵N的列向量顺序如式(18):
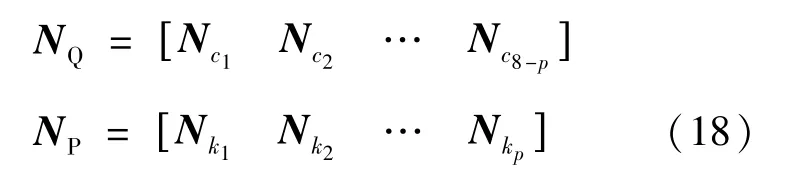
因此,式(8)可改写为式(19):
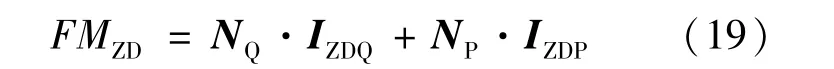
按照3.1节拉格朗日乘子法计算电流IZDQ,如式(20)所示:

3.3 饱和电流处理
若二次优化的分配电流均在电流边界范围内,则采用式(20)计算分配电流结果;否则采用式(13)计算分配电流,并进行限幅处理。有两种分配电流限幅处理方案:方案A是将超出电流边界的电流值设定为电流边界值,其余电流不变,如式(14)所示;方案B是将分配电流绝对值中的最大值设定为电流边界值,其余电流按该比例缩小,如式(21)所示:
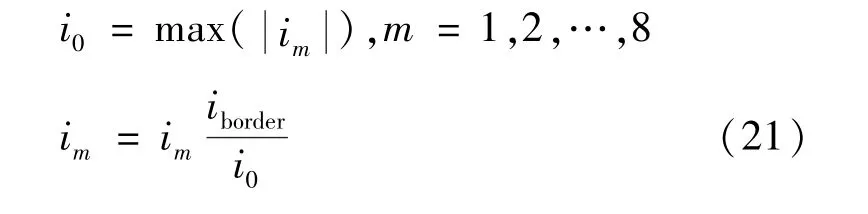
4 误差分析
为保证主动隔振控制性能指标,执行机构输出精度要求如下:
1)输出力常值偏差ΔFzdconst不大于1 mN,输出力矩常值偏差ΔMzdconst不大于0.1 N·mm;
2)输出力和力矩随机误差用高斯白噪声表征,均值为0,输出力标准差ΔFzdrand不大于1mN,输出力矩标准差ΔMzdrand不大于0.1 N·mm。
八激励器输出对浮子质心的作用力和力矩,输出误差产生的原因包括:模型误差、安装误差、浮子质心位置测量误差以及线圈的输入电流误差。
模型误差是指单个激励器输出力和输入电流按一次拟合得到的数学模型与实际模型之间的偏差,表现为系数矩阵L Bm的测量误差,该误差将同时引起激励器对浮子质心的输出力和力矩误差。
根据激励器输出力数学模型(6)可知,安装误差和浮子质心位置测量误差与输出力无关,仅与对浮子质心作用力矩的力臂计算相关,如式(5)所示。
通电线圈的输入电流误差直接影响激励器输出力的精度,如式(3)所示,将同时引起激励器对浮子质心的输出力矩误差。
在分析激励器各项误差对执行机构输出误差的影响时,采用变参数分析方法,单独加入某一误差而忽略其余误差,考察其对主动隔振控制系统执行机构输出力和力矩的影响。
4.1 模型误差
八激励器分配电流计算模型中,L和B以乘积的形式存在。工程上,L和B不是分开测量,而是得到二者的乘积。因此,统一考虑二者的乘积误差对激励器输出误差的影响。
二者乘积误差产生的原因包括:1)由于测量仪器精度引起的测量误差;2)数据拟合处理产生的模型误差。因此模型误差可以用常值偏差ΔL Bmconst和高斯白噪声标准差ΔL Bmrand表征,则实际激励器输出力计算模型系数L Bmreal如式(22):

根据式(13)可得实际解算得到的八激励器分配电流,代入式(8)可得八激励器对浮子质心的合力(S)Fzd和合力矩(F)Mzd如式(23):
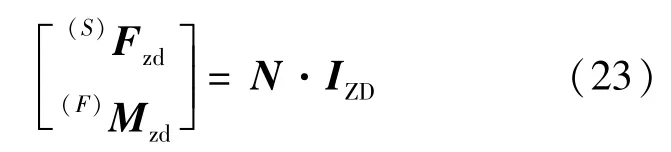
由此,可得激励器输出误差如式(24):
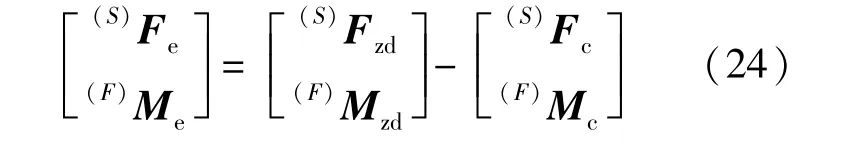
数值仿真分析模型误差引起的激励器输出力和力矩误差流程图如图4所示。
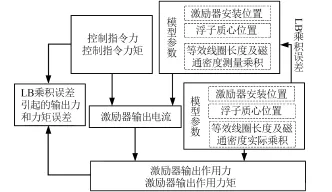
图4 L和B乘积误差引起激励器输出误差计算流程图Fig·4 Flow diagram of actuator output error caused by the product of L and B
4.2 力臂误差
从式(5)可知,激励器安装位置误差和浮子质心位置测量误差引起激励器输出对浮子质心力矩的力臂计算误差,该误差为常值偏差,用表示,则实际力臂可以表示为式(25):

数值仿真分析力臂误差引起的激励器输出力和力矩误差流程图如图5所示。
4.3 电流误差
通过式(13)计算得到激励器期望电流为IZD,实际输出存在常值误差ΔIZDconst和随机噪声误差ΔIZDrand,随机噪声误差用matlab中rand()函数生成,则实际输入电流如式(26):

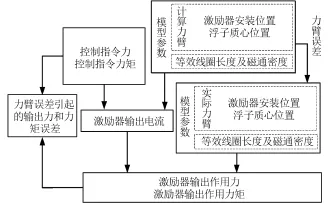
图5 力臂误差引起的激励器输出力和力矩误差流程图Fig·5 Flow diagram of actuator output error caused by measurement error of force arm
数值仿真分析激励器输入电流误差引起的激励器输出力和力矩误差流程图如图6所示。

图6 输入电流误差引起的激励器输出误差计算流程图Fig·6 Flow diagram of actuator output error caused by input current error
5 仿真
设计如下仿真参数:
1)考虑到主动隔振装置在工作状态时执行机构输出力和力矩与脐带线预紧力和预紧力矩大小相当,因此选择控制指令力和力矩如式(27)所示:


3)浮子质心在F下的坐标表示(F)rFcF0为式(29):
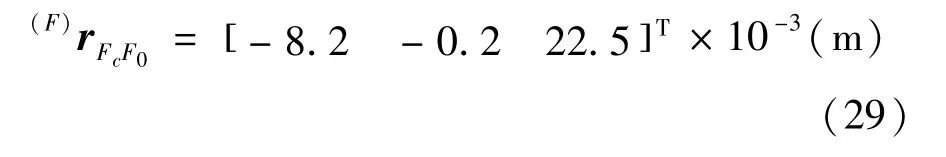
4)仿真时间1 s,采样频率1000 Hz。
5.1 无电流有界约束
无电流有界约束下仿真结果如图7~9所示。

图7 八激励器分配电流优化计算结果Fig·7 Optimization result of assignment current of eight actuators
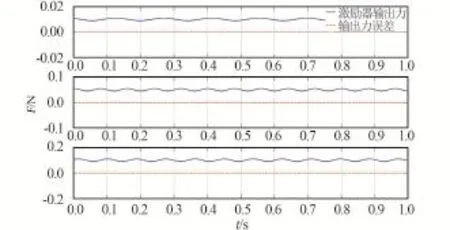
图8 激励器输出力及误差Fig·8 Actuator output force and its error
上述仿真结果表明,拉格朗日乘子法可以实现八激励器输出力/力矩零误差,并且输入电流连续平稳变化,工程上是可实现的。
为验证拉格朗日乘子法在降低总功耗上的优势,将其与最大值最小化方法比对。本文采用matlab中的优化函数fminimax(),以八激励器电流中最大值最小为性能指标进行优化计算。在相同的输入条件下,两种方法激励器总功耗(以八激励器电流平方和表征)如图10所示。
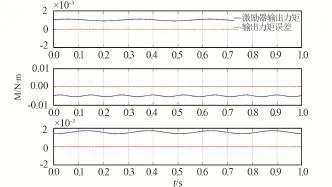
图9 激励器输出力矩及误差Fig·9 Actuator output torque and its error
图10 表明,同一时刻最大值最小化方法激励器电流平方和大于拉格朗日乘子法,验证了拉格朗日乘子法在降低八激励器总功耗方面的优势。
在无电流边界约束条件下,为保证激励器输出力和力矩精度要求,允许的各项误差如表1所示。

表1 激励器各项误差精度要求Table 1 Accuracy requirement of each error of in actuator
5.2 电流有界约束
考虑实际工程激励器输入电流有界,设为式(30):

为分析激励器输入电流超出电流边界的情况,选择如式(31)所示控制指令力和力矩:
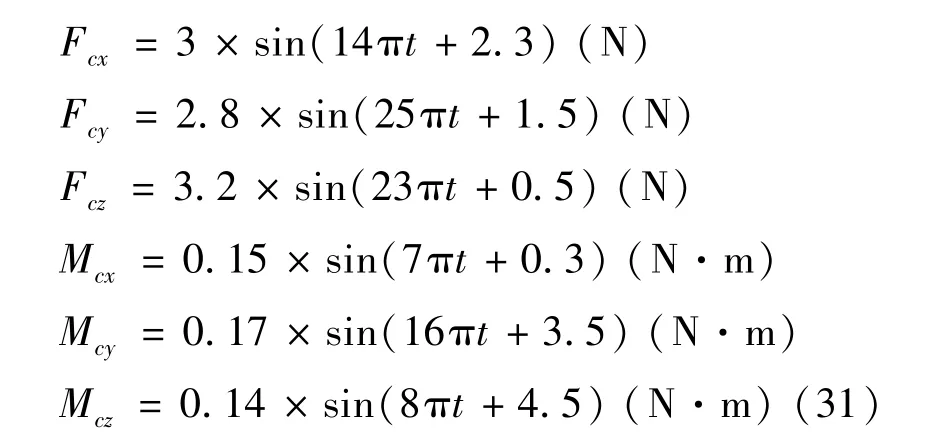
忽略各项误差,比对图11~14所示拉格朗日乘子法一次优化和二次优化、A方案和B方案激励器输出力误差。
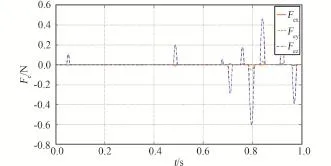
图11 拉格朗日乘子法一次优化A方案输出力误差Fig·11 The actuator output force error in once optimized Lagrange multiplier method with A program
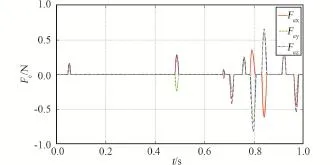
图12 拉格朗日乘子法一次优化B方案输出力误差Fig·12 The actuator output force error in once optimized Lagrange multiplier method with B program
分析上述仿真结果可知,当激励器输入电流超出电流边界约束时:1)拉格朗日乘子法二次优化相比于一次优化,能够明显降低激励器输出误差;2)A方案与B方案对比,A方案激励器输出误差小于B方案。因此,当激励器输入电流超出电流边界约束时,选用拉格朗日乘子法二次优化A方案进行八激励器分配电流设计。
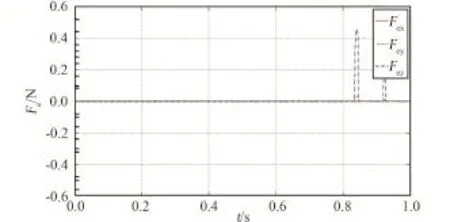
图13 拉格朗日乘子法二次优化A方案输出力误差Fig·13 The actuator output force error in twice optimized Lagrange multiplier method with A program
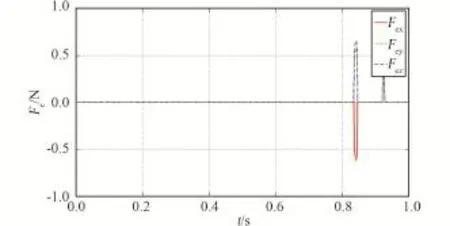
图14 拉格朗日乘子法二次优化B方案输出力误差Fig·14 The actuator output force error in twice optimized of Lagrange multiplier method used B program
6 结论
激励器输出力精度是影响主动隔振控制系统实现高微重力水平的关键因素。八激励器输出六自由度力/力矩有冗余,在保证输出控制力和力矩零误差的约束条件下,以总功耗最小为性能指标,采用拉格朗日乘子法推导获得了八激励器分配电流解析解。通过与最大值最小化方法进行仿真比对,可知拉格朗日乘子法避免了优化迭代计算过程,提高了算法效率,降低了八激励器总功耗。为进一步提高八激励器输出力的能力,当激励器输入电流超出电流边界约束时,设计了拉格朗日乘子法二次优化A方案,仿真结果验证了该方法可以有效降低激励器输出误差。最后分析了引起激励器输出力和力矩误差的各项因素,并根据主动隔振控制系统对激励器输出力和力矩精度要求,通过仿真分析得到了各项误差允许范围,为工程实践提供了依据。
References)
[1] Edberg D,Boucher R,Nurre G,et al.Performance assessment of the STABLE microgravity vibration isolation flight demonstration[C]//38th Structures,Structural Dynamics,and Materials Conference.1997:1202.
[2] Tryggvason B,Stewart W,de Carufel J,et al.Acceleration levels and operation of the microgravity vibration isolation mount(MIM)on the Shuttle and the MIR space station [C]//37th Aerospace Sciences Meeting and Exhibit,AIAA-99-05781999.
[3] NASA Facts.Active Rack Isolation System(ARIS)[R]. FS-2005-05-40-MSFC,2005.
[4] Whorton M S.g-LIMIT:A microgravity vibration isolation system for the international space station[R].AIAA 2001-5090,2001.
[5] Ren W,Li Z,Gao Y.Microgravity active vibration isolation system for space science in china[R].IAC-10-A2.5.10,Prague,CZ,IAC,2010.
[6] 王佳,于英杰,任维佳,等.高微重力振动隔离系统激励器分配优化设计[J].计算机工程与设计,2012,33(1):351-356. Wang Jia,Yu Yingjie,Ren Weijia,et al.Optimal design of assignment of actuators in space high quality microgravity active vibration isolation system[J].Computer Engineering and Design,2012,33(1):351-356.(in Chinese)
[7] 郭烨,吴文传,张伯明,等.拉格朗日乘子法电力系统网络参数错误辨识研究[J].中国电机工程学报,2013,33 (7):86-91. Guo Ye,Wu Wenchuan,Zhang Boming,et al.Power system network parameter error identification by lagrange multiplier based method[J].Proceedings of the CSEE,2013,33(7):86-91.(in Chinese)
[8] 马聪,刘哲,甄小仙.结合罚函数与序列二次规划的lp范数优化方法[J].计算机工程与应用,2013,49(18):212-216. Ma Cong,Liu Zhe,Zhen Xiaoxian.Combining penalty function with sequential quadratic programming method for lp norm minimization[J].Computer Engineering and Applications,2013,49(18):212-216.(in Chinese)
[9] 李擎,张超,陈鹏,等.一种基于粒子群参数优化的改进蚁群算法[J].控制与决策,2013,28(6):873-878. Li Qing,Zhang Chao,Chen Peng,et al.Improved ant colony optimization algorithm based on particle swarm optimization [J].Control and Decision,2013,28(6):873-878.(in Chinese)
Optimal Design of Current Distribution in Actuators in Active Vibration Isolation System
LIU Wei1,2,DONG Wenbo1,2,LI Zongfeng1,2,PENG Chao1,2
(1.Technology and Engineering Center for Space Utilization,Chinese Academy of Sciences,Beijing 100094,China;2.General Establishment of Space Science and Application,Chinese Academy of Sciences,Beijing 100094,China)
The actuator of the active vibration isolation control system consists of eight one-dimension Lorentz force actuators providing the control force and torque simultaneously in six directions. To solve the optimal problem of force distribution in eight actuators,the model of force and the model of current distribution were established and the Lagrange multiplier method was designed with the minimum total power consumption as the performance index.The analytical solution of current distribution of actuators was obtained.When the current exceeds the border,twice optimal was designed to improve the zero error output capacity of the actuator.To satisfy the accuracy requirement of the actuator,each error range allowed was analyzed.Finally,the numerical simulation showed that the Lagrange multiplier method is of smooth output,high computational efficiency and great potential application in engineering.
active vibration isolation;lorentz force actuator;current distribution;Lagrange multiplier method;twice optimal
TP302.7;V524
A
1674-5825(2015)05-0522-08
2015-01-09;
2015-07-30
刘 伟(1987-),男,硕士,工程师,研究方向为动力学与控制。E-mail:liuwei@csu.ac.cn

