PDM-CO-OFDM中采用相位传递的次符号光相位噪声抑制算法
洪学智,洪晓建,刘 柳,郭昌建
(华南师范大学华南先进光电子研究院,广州510006)
与单载波相干光通信系统相比,基于多载波的相干光正交频分复用(CO-OFDM)系统[1]可实现更灵活的频谱分配、更高效的信道均衡和更好的频谱扩展性,被认为是下一代太比特(Tbit/s)高光谱效率主干网[2-3]、长距离大容量光接入网/光城域网[4-5]的重要候选方案. 但是由于CO-OFDM 系统对光相位噪声非常敏感,其对光源线宽的容忍度较单载波相干光通信系统要低[1]. 目前认为光相位噪声影响CO-OFDM 系统的机理[6]:在接收端时域-频域转换后,其零阶频谱分量给各子载波通道带来1个随时间变化的共同相位增量(Common Phase Error,CPE),而其非零阶频谱分量在各子载波通道间引入串扰(Inter-Carrier-Interference,ICI). 若不采用适当的方法抑制光相位噪声,两者将劣化CO-OFDM系统中解调后的信号质量. 为了抑制CPE 和ICI,研究人员提出利用导频子载波引导(PA)[6-12]估计光相位噪声. PA 方案采用在发射端将部分子载波设为承载已知信息的导频子载波,通过在接收端计算导频子载波的相位与预期相位的差值,估计出光相位噪声. 在诸多PA 方案中,共同光相位噪声抑制(CPEC)方案因计算复杂度低被广泛应用[6-7]. 但CPEC 方案只能估计出单个符号内的相位噪声均值(CPE),不能够准确描述光相位噪声在符号内的变化情况. 为了减小估计误差,Pasandi 等[8]通过将相邻符号内的CPE 进行线性插值拟合(LI)以提高系统相位噪声容忍度. LI 方案是基于CPE 的时域插值,但由于求幅角值的非线性运算中存在2kπ(k 为整数)的不确定性,因此LI 只能在较小相位噪声的系统中提供优于CPEC 的性能. 从频域角度看,CPEC 方案只补偿了相位噪声的零阶分量,而忽略引起ICI 的相位噪声高阶分量. 一种抑制ICI 的可行方法是在估计光相位噪声的过程中提高时域分辨率. 高时域分辨率有助于捕捉时变的光相位噪声的高频分量,从而实现对ICI 的有效抑制. Cao 等[9]提出先基于时域分块盲估计(BL-)ICI,然后结合PA 补偿残余CPE 的光相位噪声抑制方案. 我们近期提出多个基于次符号(sub-symbol)的光相位噪声抑制方案[10-12],这些次符号方案将1个完整的CO-OFDM符号在时域分割成若干个次符号,通过判决引导在时域估计各个次符号内的共同相位噪声,从而实现高精度的相噪估计. 本文提出一种采用相位双级传递的新型次符号算法P-LI-SCPEC,并研究其在具有双倍光谱效率的偏振复用(PDM-)CO-OFDM[2]系统中的性能. 相比LI-SCPEC[11-12]算法,新算法通过将第一级的相位噪声估计结果及试探性判决一同传递给第二级,实现了更高性能的光相位噪声抑制.
1 算法原理
在PDM-CO-OFDM 接收端,光电转换后得到的信号经符号同步[13]、频差估计及信道均衡[14]后,输入到光相位噪声抑制算法模块. 图1 为本文的相位传递次符号光相位噪声抑制算法P-LI-SCPEC 的流程图.

图1 采用相位传递的次符号光相位噪声抑制算法P-LI-SCPECFigure 1 Sub-symbol optical phase noise suppression algorithm adopting phase passing P-LI-SCPEC
算法分为2 级,第1 级(stage 1)首先检测导频相位并通过最小二乘法(LS)准则估计出整个符号的CPE,然后将相邻符号的CPE 进行线性插值(LI)获得更精确的相位估计,最后将该估计值用于相位噪声补偿并进行试探性判决. 在第2 级(stage 2)中,首先将第1 级的试探性判决结果与判决前的信号分别在时域上分割成若干个次符号. 通过对比这2 级算法,获得在LS 准则下各次符号内的相位噪声均值(SCPE).
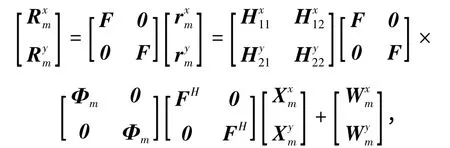
其中,F 和FH分别为DFT 和离散傅立叶逆变换(IDFT)矩阵,为传输过程中光放大器引入的放大自发辐射(ASE)噪声,H =为光纤信道的传输矩阵的频域表达式,为发射端频域加载的数据,对角矩阵为时变的光相位噪声向量. 信道均衡后的时域样本可以表示为

通过线性插值得到的粗相位估计值为
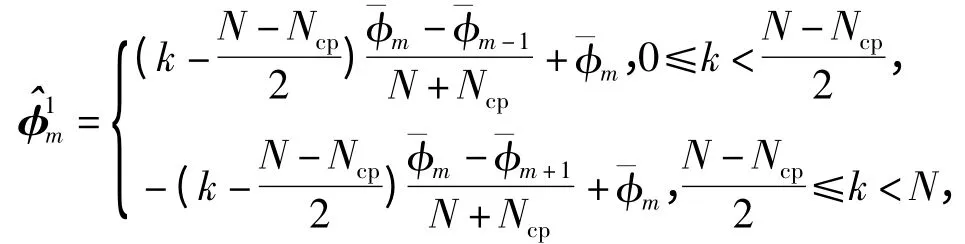

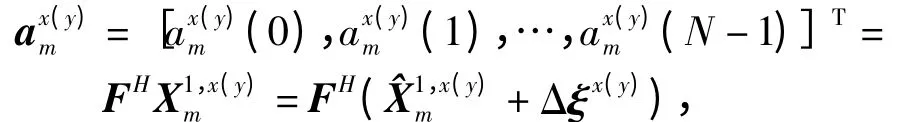
其中Δξx(y)为判决误差,Q(·)为判决操作. 若将单个符号切割成NB个次符号,则第1 级中判决前的第n个次符号所对应的时域样本可以表示为
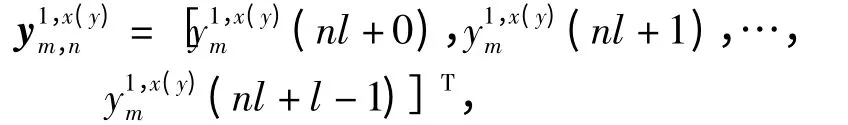
这里0≤n≤NB-1,l =N/NB为每个次符号的长度.类似的,“预估”的时域样本也被分割成NB个
次符号,其中第n个次符号样本为
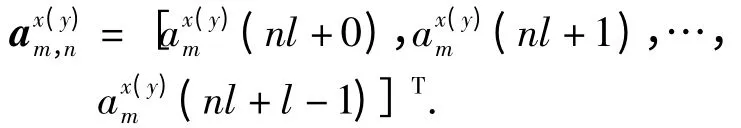
光相噪向量可以用次符号的形式表示为

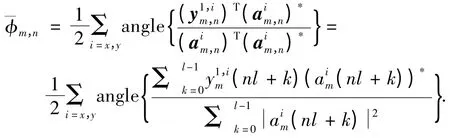
与前期研究[11-12]提出的次符号LI-SCPEC 算法相比,LI-SCPEC 中将信道均衡后的样本作为第2 级次符号处理的输入,而新算法第2 级次符号处理的输入是第1 级传递来的粗相位补偿后的样本. 新算法降低了第2 级相位“待估计”的相噪方差,有助于提升第2 级估计的精度.
2 蒙特卡洛仿真结果
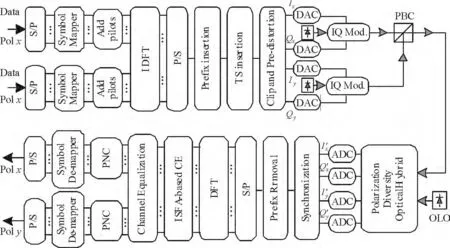
图2 PDM-CO-OFDM 仿真系统框图Figure 2 Schematic diagram of the simulated PDM-CO-OFDM system
通过蒙特卡洛仿真研究算法的性能. 图2 为PDM-CO-OFDM 仿真系统的结构示意框图. 系统的具体参数如下:DFT/IDFT 变换点数N=256,承载数据的子载波数Ncarrier=211,空白子载波数Nnull=40(10个位于频带中央,30个位于频带两侧),导频子载波数Npilot=5(频带内均匀分布),循环前缀长度Ncp=32,DAC/ADC 采样率Rsampling为10 G/s. 系统采用了16QAM 调制格式,对应的系统有效速率为29.31 Gb/s. 激光器的光相位噪声模型为维纳过程(Wiener process). 每54个符号插入1 对训练序列进行信道估计,采用符号内频域平均(ISFA)算法[14]实现信道估计,频域平均参数m=2.
图3 给出了1个特定光相位噪声样本时,采用不同光相位噪声抑制算法的系统的星座图. 由于PLI-SCPEC 算法采用的是前向(feed-forward)结构,图3 可视为P-LI-SCPEC 算法的光相位噪声估计过程中不同阶段(CPEC、LI 对应第1 级)的输出. P-LISCPEC 算法的输出信号比CPEC 及LI 具有更小的残余ICI.

图3 不同算法系统在光源线宽为250 kHz 时输出的星座图Figure 3 Constellation of recovered signal with different algorithms under a combined laser linewidth of 250 kHz
图4 给出了光源综合线宽为350 kHz 时,采用不同算法时系统误码率(BER)与光信噪比(OSNR)的关系图. 得益于高性能的ICI 抑制(BER =1.0 ×10-3),在同样的切割数目下(NB=2 或4),系统采用P-LI-SCPEC 比BL-ICI 能获得1.35 dB (NB=2)和1.40 dB(NB=4)的OSNR 增益. 相比前期研究提出的LI-SCPEC 算法,在切割数目较小(NB=2)时新算法提供了0.2 dB 的OSNR 增益,而在切割数目较大(NB=4)时,两者性能几乎相同.
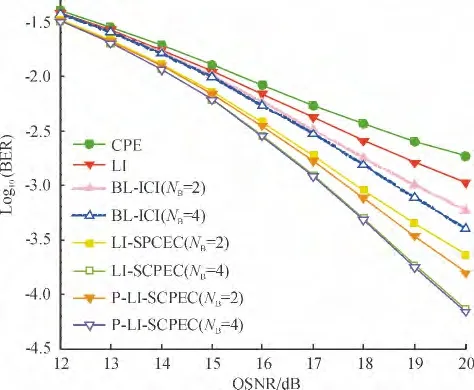
图4 不同算法系统在光源线宽为350 kHz 时的BER 与OSNR 关系图Figure 4 BER versus OSNR for system using different algorithms under a combined laser linewidth of 350 kHz
为达到BER=1.0 ×10-3,采用不同算法系统所需要的OSNR 与光源线宽的关系如图5 所示. 在特定OSNR 下,新算法(NB=4)能提供更大的光源线宽容忍度. 当OSNR =20 dB 时,P-LI-SCPEC(NB=4)能提供的线宽容忍度约为770 kHz,分别是算法CPEC、LI、BL-ICI(NB= 2)、BL-ICI(NB= 4)、LISCPEC(NB=2)及P-LI-SCPEC(NB=2)的2.87、2.23、1.73、1.35、1.34 和1.2 倍. 值得注意的是,新算法虽然与算法LI-SCPEC(NB=4)的性能接近,但是其优势随着线宽的增加而变大.
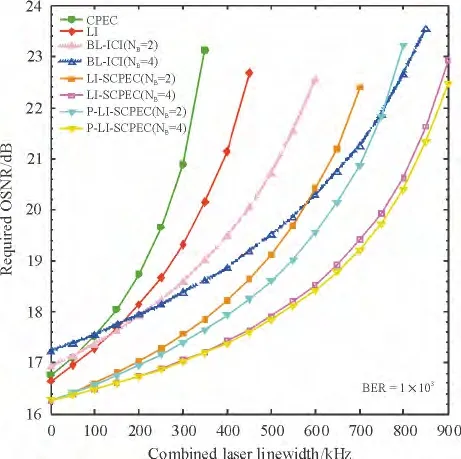
图5 不同算法系统在BER =1.0 ×10 -3 时所需OSNR 与光源线宽的关系Figure 5 Required OSNR in system with different algorithms for BER=1.0 ×10 -3 under different laser linewidths
前述结果表明,NB的取值(2 或4)对算法的性能产生了明显的影响. 进一步研究算法性能对NB的依赖性. 图6 给出了BER=1.0 ×10-3时,不同的次符号数目、不同光源线宽下所对应的OSNR 梯度图. 对于特定的OSNR,系统的线宽容忍度随NB增加经历了先增后减的过程. 换言之,存在1个最佳的NB使得系统的光源线宽容忍度最大. 而对于特定的光源线宽,存在1个NB使得系统所需OSNR 最小. 同时,随着光源线宽的增加,最佳的NB取值逐渐变大.
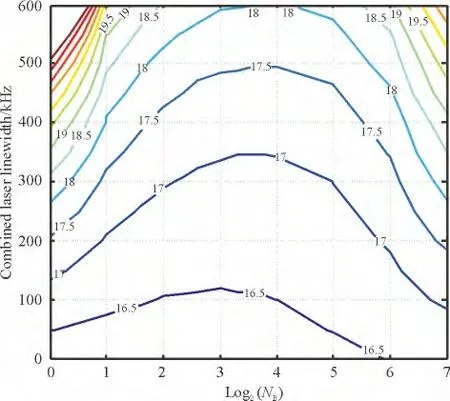
图6 不同NB、不同光源线宽系统在BER =1.0 ×10 -3 时所需OSNR 的梯度图Figure 6 Contour plots of OSNR with different NB and different laser linewidths for BER=1.0 ×10 -3
3 结论
提出一种采用相位传递的次符号光相位噪声抑制算法P-LI-SCPEC,并通过蒙特卡洛仿真研究了其在PDM-CO-OFDM 系统中抑制光相位噪声的性能.结果表明,与已有的几种光相位噪声抑制算法(CPEC、LI、BL-ICI 及LI-SCPEC)相比,新算法能提供更大的光源线宽容忍度. 此外,还发现算法性能受次符号数目NB影响,并且存在1个最佳次符号数目NB使得算法的性能最优. 高性能的P-LISCPEC 算法对于推动PDM-CO-OFDM 技术在大符号周期-光源线宽乘积和采用高阶调制格式的光网络中的应用具有重要意义.
[1]Shieh W,Djordjevic I. OFDM for optical communications[M]. New York,USA:Academic Press,Elsevier,2010:19-22.
[2]Yang Q,Amin A Al,Chen X,et al. 428-Gb/s singlechannel coherent optical OFDM transmission over 960-km SSMF with constellation expansion and LDPC coding[J].Optics Express,2010,18(16):16883-16889.
[3]Yi X,Fontaine N K,Scott R P,et al. Tb/s coherent optical OFDM systems enabled by optical frequency combs[J]. Journal of Lightwave Technology,2010,28(14):2054-2061.
[4]Cvijetic N,Huang M F,Ip E,et al. 1.92 Tb/s coherent DWDM-OFDMA-PON with no high-speed ONU-side electronics over 100km SSMF and 1∶64 passive split[J]. Optics Express,2011,19(24):24540-24545.
[5]Cvijetic N,Huang M F,Ip E,et al. Coherent 40 Gb/s OFDMA-PON for long-reach (100 +km)high-split ratio(1∶64)optical access/metro networks[C]∥Proceeding of optical fiber communication conference. Los Angeles,USA:The Optical Society of America,2012:OW4B.
[6]Yi X,Shieh W,Ma Y. Phase noise effects on high spectral efficiency coherent optical OFDM transmission[J].IEEE Journal of Lightwave Technology,2008,26(10):1309-1316.
[7]Yi X,Shieh W,Yan T. Phase estimation for coherent optical OFDM[J]. IEEE Photonics Technology Letters,2007,19(12):919-921.
[8]Pasandi M,Zhuge Q,Xu X. Experimental demonstration of non-iterative interpolation-based partial ICI compensation in 100 G RGI-DP-CO-OFDM transport systems[J].Optics Express,2012,20(14):14825-14831.
[9]Cao S,Kam P Y,Yu C. Time-domain blind ICI mitigation for non-constant modulus format in CO-OFDM[J].IEEE Photonics Technology Letters,2013,25 (24):2490-2493.
[10]Hong X,He S. Sub-frame carrier phase estimation for coherent optical orthogonal frequency division multiplexing system[C]∥Progress in electromagnetics research symposium (PIERS). Stockholm,Sweden,2013.
[11]Hong X,Hong X,He S. Sub-symbol based carrier phase recovery in CO-OFDM system with linear interpolation[C]∥Progress in electromagnetics research symposium(PIERS). Guangzhou,China,2014.
[12]Hong X,Hong X,He S. Linearly interpolated sub-symbol optical phase noise suppression in CO-OFDM system[J]. Optics Express,2015,23(4):4691-4702.
[13]Schmidl T M,Cox D C. Robust frequency and timing synchronization for OFDM[J]. IEEE Transactions on Communications,1997,45(12):1613-1621.
[14]Liu X,Buchali F. Intra-symbol frequency-domain averaging based channel estimation for coherent optical OFDM[J]. Optics Express,2008,16(26):21944-21957.

