地基雷达部署对探测临近空间高超声速目标影响研究

肖 松 谭贤四 王 红 曲智国

1 引言

临近空间高超声速飞行器是指在临近空间（距离地面20～100 km）飞行速度达到5 Ma（1 Ma表示1倍声速）以上的飞行器[1,2]。具有飞行高度高、飞行速度快、机动能力强、打击威胁大等特点，应用前景十分广阔[3,4]。近年来，临近空间高超声速飞行器的政治、经济和军事价值逐渐引起各国高度重视，并成为美俄等军事强国的研究热点[5]。随着临近空间高超声速飞行器的快速发展，对该类目标的防御变得越来越紧迫[6,7]。因此，开展 GBR部署对探测临近空间高超声速飞行器影响的研究，对构建临近空间预警系统具有指导意义。

针对常规目标GBR部署方式的研究较为成熟，文献[8]针对雷达网节点部署问题，提出了正六边形和钻石形部署策略；文献[9]建立了圆形、线形和扇形部署模型，研究了目标联合检测概率问题；文献[10,11]分别使用基于潜在博弈的分布式算法和遗传算法实现组网雷达的优化部署；文献[12]以覆盖系数和重叠系数为主要优化目标，基于NSGA-Ⅱ算法进行多目标优化，从全局出发引导雷达网优化部署，提高算法收敛性。但是，对于临近空间高超声速目标，GBR以何种部署方式可实现最优探测的研究鲜见报道。鉴于此，本文针对临近空间高超声速目标的雷达特性，提出雷达探测性能评估指标，为GBR探测临近空间高超声速目标的优化部署提供理论依据和技术支撑。

2 问题描述

2.1 GBR部署方式

传统 GBR部署方式主要有前沿部署、接力部署和要地部署，其示意图如图1所示。

前沿部署适合敏感地区和边境一线，是世界多数国家预警力量的主要部署方式，能够获得更充足的预警时间，同时拓展作战空间，为防御系统提供更多拦截准备时间；接力部署是按来袭目标飞行航迹以远程、中程、近程配备预警力量的部署方式，能够提高预警情报的连续性和准确性；要地部署是以重要地区为圆心，采用多种预警装备形成交叉重叠环形的部署方式，能够对重要区域形成严密覆盖，有效降低漏警和虚警概率。

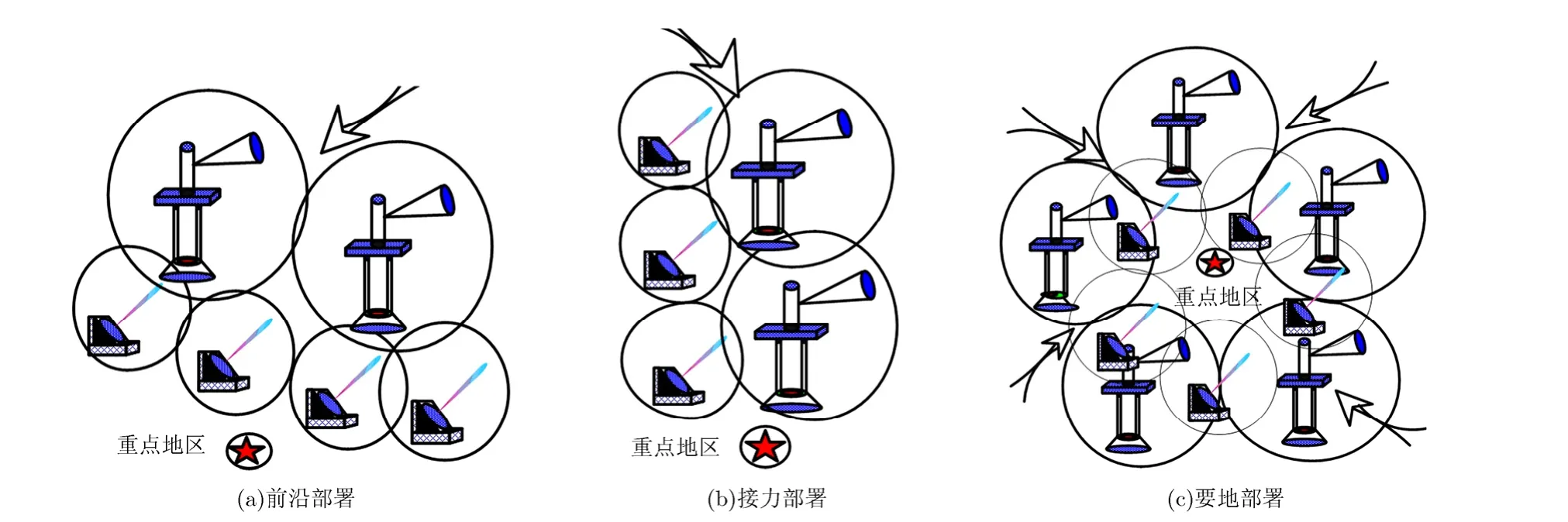
图1 GBR部署方式示意图

2.2 临近空间高超声速目标运动模型

考虑垂直平面内飞行的临近空间高超声速目标，其主要受到重力mg、推力P、升力L和阻力D的合力Q，在直角坐标系中的运动受力示意图如图2所示。

在图 2中，A1B1段、B1C1段和 C1D1段分别为助推爬升段、平飞巡航段和俯冲攻击段，目标所受推力、阻力等的方向和大小随着飞行阶段的变化而变化。假设某时刻目标飞行高度为h、速度为v、航迹倾角为γ、攻角为ψ、飞行器质量为m、地球产生的引力加速度为g、地球半径R=6371 km，则

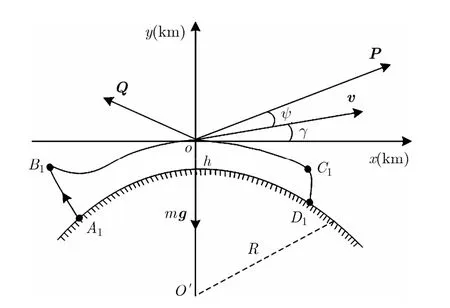
图2 目标运动受力示意图

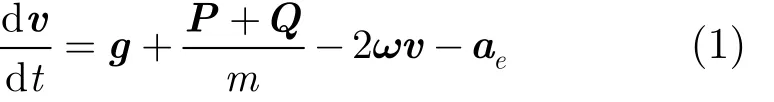
其中ω为目标角速度，ea为牵连加速度。

（2）航向变化：为了确保飞行器飞行方向一直朝着目标，飞行器速度方向（航向）与其指向目标方向之间的夹角小于90°，并且，

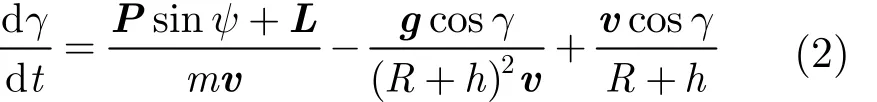
（3）机动能力：飞行器发动机的特殊要求造成可用过载限制严格，转弯半径比常规目标的大，其绝对加速度ia和最大转弯半径maxr 受约束为[13]

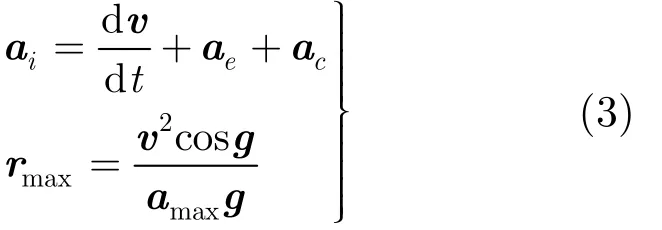
3 GBR对临近空间高超声速目标探测性能分析

3.1 临近空间高超声速目标RCS模型

飞行器在高超声速飞行时，在飞行器周围形成等离子体（或电离气体）包覆流场[14]，使电磁波产生折射、反射或散射，同时吸收电磁波能量，从而影响目标RCS特性。

等离子体对目标 RCS的影响主要由电磁波在等离子体中传播的衰减和反射因子决定。由文献[15]可得，单位距离衰减lA为

其中f为雷达频率，

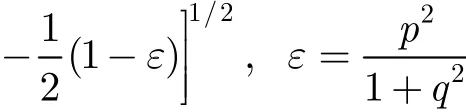
v等离子体厚度为10 cm，此时双程衰减为20 cm，不同目标速度和电子碰撞频率下的回波总衰减和衰减等值线分别如图3和图4所示。

由图3可得，X波段（9 GHz）条件下，回波总衰减最严重时达到25 dB。以美国HTV-2飞行器为例，对应X波段（9 GHz）RCS姿态响应如图5所示。

在图5中，姿态角的零度方向为目标的鼻锥方向，在X波段HH极化和VV极化下的RCS姿态响应在180°处有最大值，为目标尾部的反射，姿态角在0°至360°之间出现3个峰值，分别对应目标的3个反射面，其它范围内低于-10 dBsm。

3.2 雷达探测临近空间高超声速目标模型

GBR的作用距离方程为

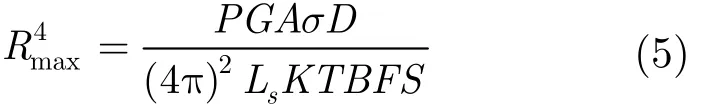
其中 Rmax为在m个脉冲积累后达到接收机检测目标所需最小信噪比S时，对RCS为σ目标的最远探测距离，P为发射机功率，G为天线增益，A为天线面积，D为时宽带宽积，Ls为雷达系统损耗和目标起伏损耗，K为玻尔兹曼常数，T为等效噪声温度，F为噪声系数，B为带宽。对于给定距离和RCS的目标，地基雷达的测量信噪比为

3.3 探测性能评估指标

（1）检测概率 根据GBR的作用距离方程，可计算检测到距离R处目标所需的最小信噪比S，并根据随机信号检测理论推算既定虚警概率时的检测概率。探测概率与积累脉冲数m、检测门限TV （由虚警概率fP确定）和信噪比有关，具体公式为[17]

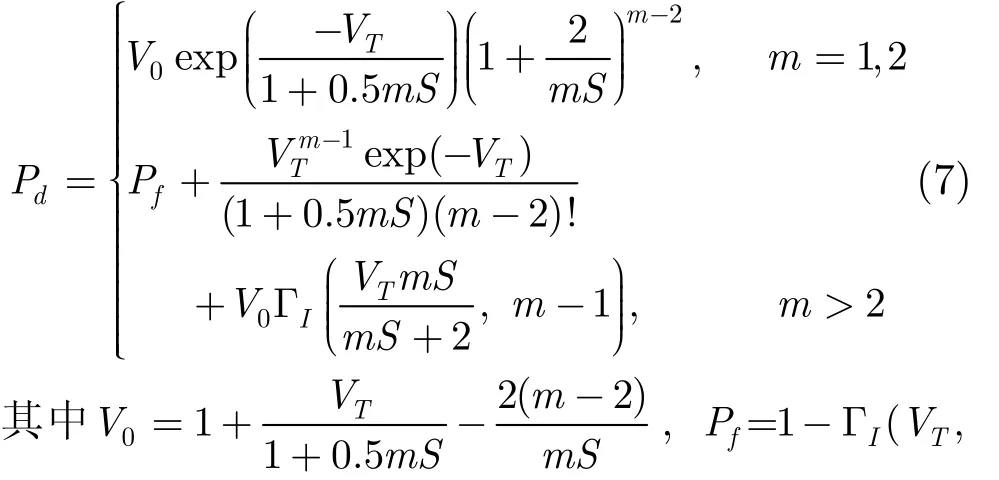
m- 1 ）, ΓI（⋅） 为不完全 γ 函数：

雷达探测临近空间高超声速目标时一般会产生距离走动和多普勒走动，需要对回波信号进行相关的速度及加速度补偿，实现脉冲的有效积累[18]。采用Newton-Raphson递归方法可对门限进行近似求解。

由前面建立的临近空间高超声速目标运动模型和 RCS模型，结合雷达探测模型可得到目标 RCS及探测距离随观测时间的变化情况，通过式（7）计算出雷达对目标的检测概率与虚警概率、积累脉冲数和信噪比的关系，用于雷达检测性能的分析。

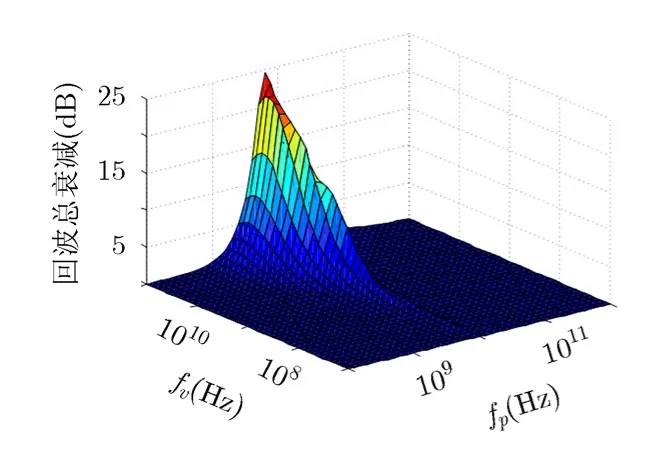
图3 回波总衰减

图4 衰减等值线

图5 RCS姿态响应

（2）跟踪系数 雷达网对目标信息掌握的及时性、连续性和严密性是进行稳定跟踪的前提。从预警时间考虑，要求雷达网越早发现目标越好；从空域覆盖考虑，确保在各高度层都能连续覆盖，对典型高度层能够严密覆盖；从衔接区域考虑，相邻雷达在尽可能小的衔接区域内能够实现稳定交接；从资源冗余考虑，在可能的目标来袭方向应多重覆盖，并实现探测资源的优化部署。所以跟踪系数定义为

其中 K1+ K2+ K3+ K4= 1 , K1, K2, K3和 K4可根据我方战略意图和来袭目标类型确定。 Li为第i部雷达发现目标时，目标与保护对象之间的距离，Ld为目标射程，雷达网内共有N部雷达，雷达对目标的发现距离越大，则其探测能力越强。 Sa为责任区总面积， Rij为第 i（1 ≤ i≤N） 部雷达在第j（1≤j≤ M ）个高度层上的作用距离，则第i部雷达在第j个高度层上的覆盖面积为 Sij=π。Sj为相邻雷达单元在高度层j上的探测威力重叠区域面积， Ss为探测半径较小雷达单元的探测区域面积，Pdi为单部雷达对临近空间高超声速目标的检测概率，为融合后的检测概率。在单部雷达检测概率一定时，雷达数目越多，则融合后的检测概率越高，空域覆盖严密性越好，雷达网能够进行稳定跟踪的能力就越强。

（3）资源冗余率 资源冗余率表示雷达网在满足作战需求时，探测资源的冗余程度。定义k时刻雷达网探测目标的资源冗余率为

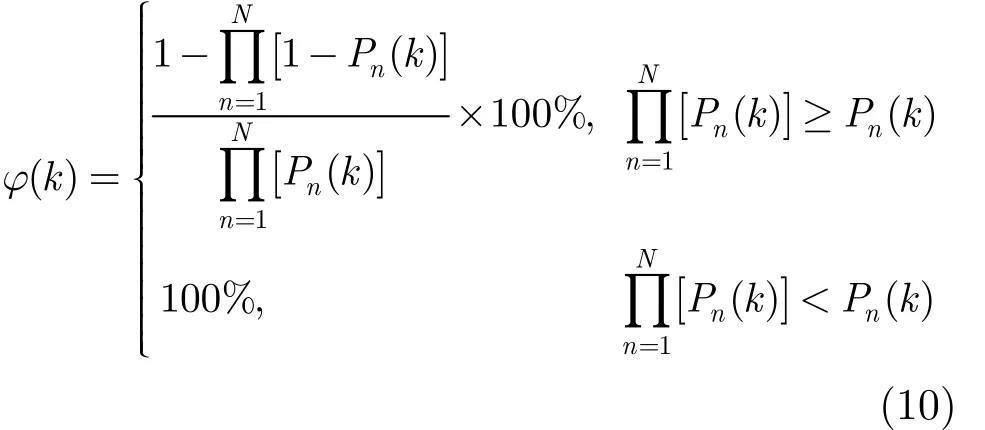
其中0 ＜ φ（k）≤ 100%, φ（k）越小表明雷达冗余资源越少，N为雷达总数量， Pn（ k）表示第n部雷达在k时刻对临近空间高超声速目标的探测概率，如果在“或”法则下，雷达网总的探测概率小于单部雷达探测概率，则认为雷达网很难有效探测到目标，此时资源冗余率为100%。

临近空间高超声速目标飞行速度极快，打击威胁大，在雷达探测此类目标全过程中，在工程实践中认为，若在一定虚警概率条件下，探测概率大于0.90时可实现对目标的有效监测，跟踪系数大于0.80时可实现对目标的稳定跟踪，资源冗余率大于75%时存在探测资源冗余。因此，GBR部署是希望利用最少的雷达资源，实现对临近空间高超声速目标的有效检测和稳定跟踪。

4 仿真分析

考虑实际作战需求，GBR无法部署在临近空间高超声速目标发射点后方或者附近，采用前沿部署、接力部署和要地部署的方式，在目标（HTV-2）轨道平面及其侧面部署雷达，GBR部署（转换到直角坐标系中）示意图如图6所示。

图6中，临近空间高超声速目标发射点为（1000,2000,10），落点为（6597,2000,0）（单位：km）。临近空间高超声速目标飞行过程中，雷达观测角变化曲线如图7所示。

假设GBR的探测方位为360°，仰角3°～75°，则目标在飞行过程中会穿过雷达的顶空盲区，从图7中可以看出，目标穿过弹道平面内雷达顶空盲区的时间要长于弹道平面外的。雷达视线与目标飞行方向之间的夹角如图8所示。

从图8中可以看出，雷达视线与目标飞行方向之间的夹角均在 0°～180°范围内，且在巡航段，弹道平面内的雷达与目标飞行方向之间的夹角会急剧增加，而弹道平面外的则增加较缓慢，GBR4部署在落点前方，故其与目标飞行方向的夹角一直较小，变化的动态范围也较小。

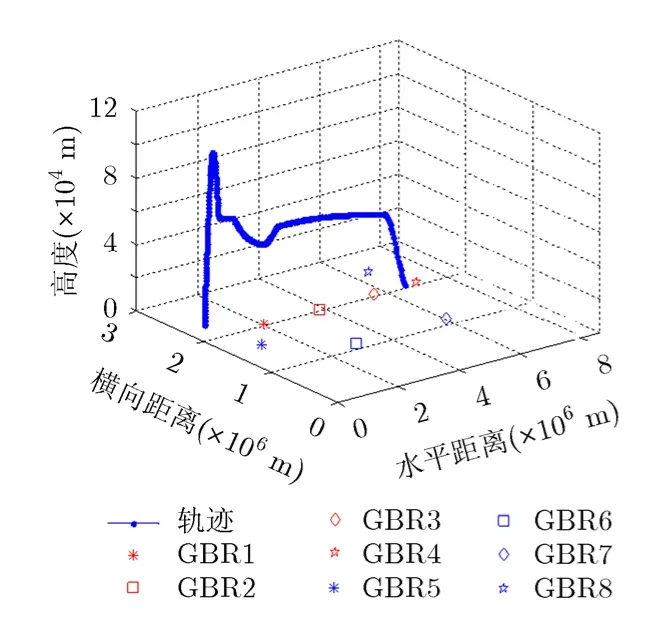
图6 GBR部署位置示意图

图7 雷达观测角变化曲线

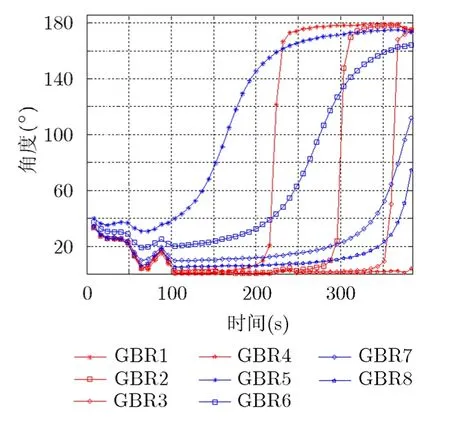
图8 雷达视线与目标飞行方向夹角

假设雷达虚警概率为 1 0-6，多脉冲检测时，对RCS为 1 m2的临近空间高超声速目标探测距离可达1300 km。不同雷达组合情况下的检测概率如图9和图10所示。

从图9和图10中可以看出，前沿部署的雷达（GBR1和 GBR5），其检测概率在目标发射后至巡航中段较高；接力部署的雷达（GBR2和 GBR3）受到顶空盲区的影响，其检测概率存在断续现象；目标在俯冲攻击阶段的时间短，且运动状态变化较大，导致要地部署的雷达（GBR7和 GBR8）能够有效检测的时间短。3部雷达组合时，其检测概率要优于两部雷达组合的情况，特别是弹道平面外的部署（GBR5, GBR6和GBR7）, GBR5部署位置靠前，而GBR6和GBR7充分发挥其探测性能，没有受到顶空盲区的影响，能够对临近空间高超声速目标进行较长时间有效检测。表1列出了不同雷达组合的跟踪系数（表中H为目标高度）。

从表1中可以看出，随着目标高度的增加，跟踪系数有增大的趋势，3部雷达组合的跟踪系数大于两部雷达组合的，这是因为随着高度的增加，雷达覆盖范围在增加，相邻雷达重复覆盖区域增加，提高了雷达跟踪能力。3部雷达组合时，GBR5,GBR6和GBR7的组合优于其它两种情况，这是因为GBR1, GBR2和GBR3都在弹道平面内，3个顶空盲区导致跟踪出现断续的情况，而GBR3, GBR7和 GBR8的组合中，首次发现目标的距离较近，GBR7和GBR8在俯冲攻击段的重复区域较大，导致有效跟踪区域减小。不同雷达组合情况下的资源冗余率如图11和图12所示。

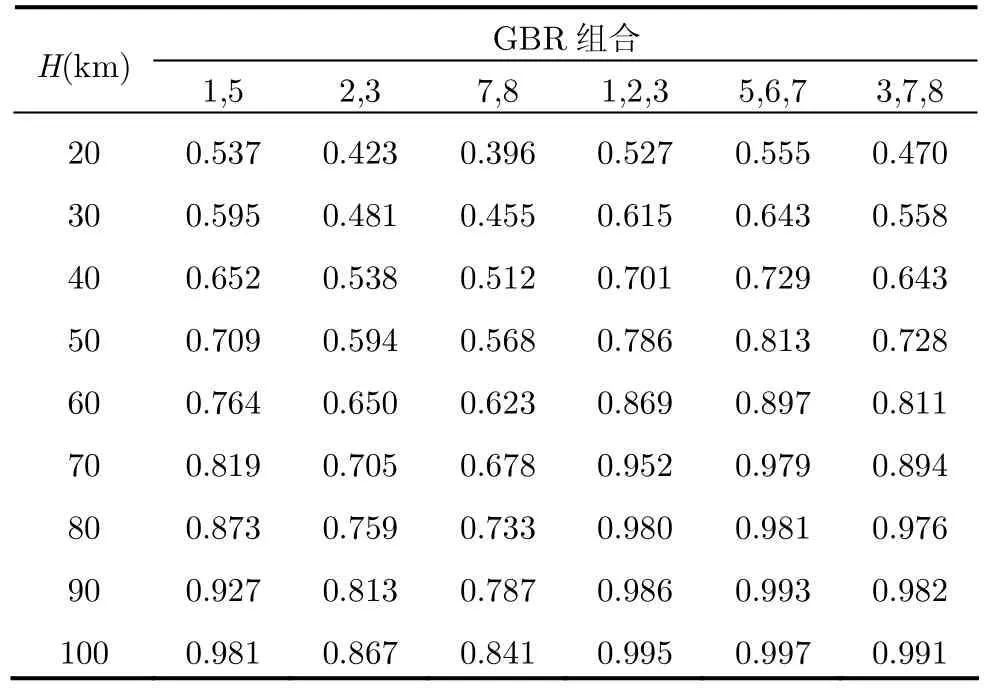
表1 跟踪系数

从图11和图12中可以看出，两部雷达组合的资源冗余率为100%的情况多于3部雷达组合的，即说明两部雷达组合有较多情况不能对临近空间高超声速目标进行有效探测，而3部雷达组合情况中，GBR5, GBR6和GBR7的组合优于其它两种情况，其它两种组合情况受到顶空盲区和过多重叠覆盖区域的影响，导致雷达资源利用率降低。

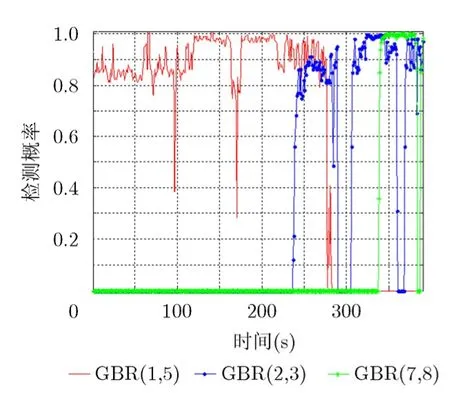
图9 两部雷达检测概率

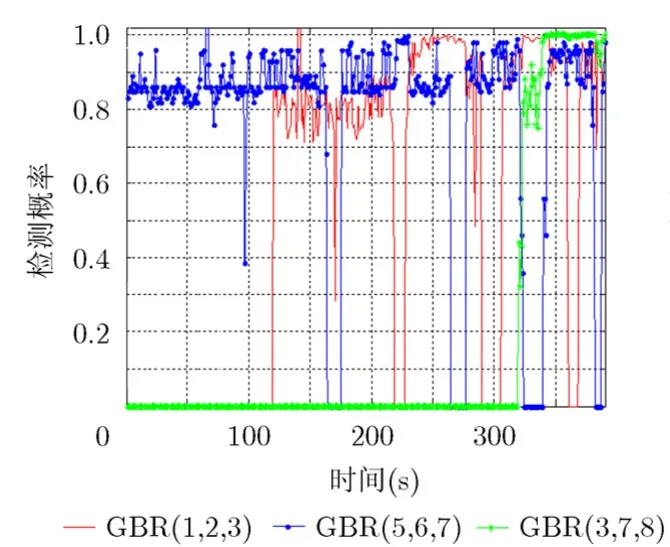
图10 3部雷达检测概率

图11 两部雷达资源冗余率

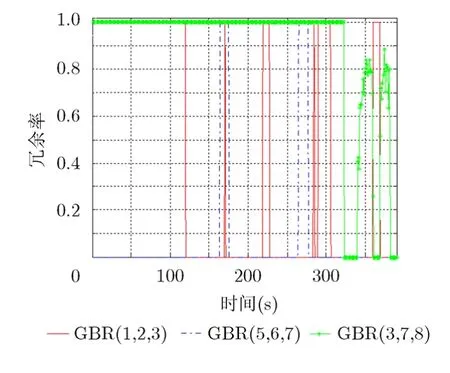
图12 3部雷达资源冗余率

5 结束语

本文建立了临近空间高超声速目标模型和GBR探测模型，提出检测概率、跟踪系数和资源冗余率3种雷达探测性能评估指标，研究GBR部署方式对探测临近空间高超声速目标的影响，仿真结果表明：（1）弹道平面外部署的GBR探测性能比弹道平面内的好；（2）对雷达分布设计，采用接力部署和前沿部署相结合的方式，即加强海基雷达和边境线附近的雷达部署，同时增加重点来袭方向的覆盖次数；（3）在GBR优化部署时，要尽可能有前置部署，增大首次发现距离，在拦截点两侧要有适当的空域覆盖冗余度，以提高稳定跟踪能力。如何实现GBR快速有效部署将是下一步的研究重点。

[1] 朱志良, 叶宁, 刘军, 等. 基于临近空间飞行器的区域自组网优化部署算法[J]. 电子与信息学报, 2011, 33（4）: 915-920.Zhu Zhi-liang, Ye Ning, Liu Jun, et al.. Deployment optimization algorithm for regional MANET containing near space vehicles as a part[J]. Journal of Electronics &Information Technology, 2011, 33（4）: 915-920.

[2] 肖松, 谭贤四, 王红, 等. 临近空间高超声速目标断续点迹航迹起始方法[J]. 华中科技大学学报（自然科学版）, 2014, 42（3）:52-57.Xiao Song, Tan Xian-si, Wang Hong, et al.. Feasible track initiation method for near space hypersonic target[J]. Journal of Huazhong University of Science and Technology （Natural Science Edition）, 2014, 42（3）: 52-57.

[3] 曾开春, 向锦武. 高超声速飞行器飞行动力学特性不确定分析[J]. 航空学报, 2013, 34（4）: 798-808.Zeng Kai-chun and Xiang Jin-wu. Uncertainty analysis of flight dynamic characteristics for hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34（4）: 798-808.

[4] Zhao Jing, Jiang Bin, Shi Peng, et al.. Adaptive dynamic sliding mode control for near space vehicles under actuator faults[J]. Circuits System and Signal Processing, 2013, 32（5）:2281-2296.

[5] Huang Wei, Ma Lin, and Wang Zhen-guo. A parametric study on the aerodynamic characteristics of a hypersonic waverider vehicle[J]. Acta Astronautica, 2011, 69（3/4）:135-140.

[6] 李罗钢, 荆武兴, 高长生. 基于预警卫星系统的临近空间飞行器跟踪[J]. 航空学报, 2014, 35（1）: 105-114.Li Luo-gang, Jing Wu-xing, and Gao Chang-sheng. Tracking near space vehicle using early-warning satellite[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35（1）: 105-114.

[7] 汪连栋, 曾勇虎, 高磊, 等. 临近空间高超声速目标雷达探测技术现状与趋势[J]. 信号处理, 2014, 30（1）: 72-85.Wang Lian-dong, Zeng Yong-hu, Gao Lei, et al.. Technology status and development trend for radar detection of hypersonic target in near space[J]. Journal of Signal Processing, 2014, 30（1）: 72-85.

[8] Ling Yang, Jing Liang, and Liu Wei-wei. Graphical deployment strategies in radar sensor networks （RSN） for target detection[J]. EURASIP Journal on Wireless Communications and Networking, 2013, 2013（1）: 1-9.

[9] Gao Shang. Optimal deployment problems of radar network[J]. Research Journal of Applied Sciences Engineering and Technology, 2013, 6（10）: 1879-1883.

[10] 李奇. 基于分布式算法的雷达组网抗干扰优化部署研究[D].[硕士论文], 西安电子科技大学, 2013.Li Qi. Research on optimized anti-jamming development model of radar networks based on distributed algorithm[D].[Master dissertation], Xidian University, 2013.

[11] 熊军. 基于遗传算法的雷达网优化部署研究[D]. [硕士论文],山西师范大学, 2013.Xiong Jun. Radar network deployment optimization based on genetic algorithm research[D]. [Master dissertation], Shanxi Normal University, 2013.

[12] 刘彦君, 黄金才, 王江. 有源干扰条件下基于 NSGA-Ⅱ的雷达网优化部署方法[J]. 指挥控制与仿真, 2014, 36（1）: 36-40.Liu Yan-jun, Huang Jin-cai, and Wang Jiang. Optimal deployment of radar network based on NSGA-Ⅱ under active jamming[J]. Command Control & Simulation, 2014,36（1）: 36-40.

[13] 李惠峰. 高超声速飞行器制导与控制技术[M]. 北京: 中国宇航出版社, 2012: 36-120.Li Hui-feng. Hypersonic Vehicle Guidance and Control Technique[M]. Beijing: China Astronautic Publishing House,2012: 36-120.

[14] 乐嘉陵. 再入物理[M]. 北京: 国防工业出版社, 2005: 40-98.Yue Jia-ling. Reentry Physical[M]. Beijing: National Defense Industry Press, 2005: 40-98.

[15] Marini J W. On the decrease of the radar cross section of the apollo command module due to reentry plasma effects[R].Washington: National Aeronautics and Space Administration,1968.

[16] Huber P. Hypersonic shock-heated flow parameters for velocities to 46,000 feet per second and altitudes to 323,000 feet[R]. Washington: National Aeronautics and Space Administration, 1963.

[17] 张毅, 肖龙旭, 王顺宏. 弹道导弹弹道学[M]. 长沙: 国防科技大学出版社, 1999: 261-282.Zhang Yi, Xiao Long-xu, and Wang Shun-hong. Ballistic Ballistics[M]. Changsha: National Defense University 1999:261-282.

[18] 李志淮, 谭贤四, 王红, 等. 基于运动参数估计的高超声速目标检测方法研究[J]. 宇航学报, 2012, 33（3）: 346-352.Li Zhi-huai, Tan Xian-si, Wang Hong, et al.. Detection algorithm for hypersonic targets based on motion parameter estimation[J]. Journal of Astronautics, 2012, 33（3）: 346-352.