迭代变步长LMS算法及性能分析
刘建成 赵宏志 全厚德 唐友喜
1 引言
随着信息化和现代数字技术的发展,诸多领域对信号特征提取和噪声等干扰消除的要求日趋强烈,需要能够对信号实时自适应处理。LMS(Least Mean Square)算法是在维纳-霍夫方程基础上提出的一种自适应信号处理算法,能够实现滤波、平滑和预测等处理[1]。由于LMS算法计算简单、易于实现,已被广泛应用于通信噪声控制[2]、信道均衡[3]和有源干扰对消[4]、语音回声抵消[5]以及雷达信号中的杂波消除等方面。
不过,常规的LMS算法中步长因子恒定,即定步长 LMS(Fixed Step-Size LMS, FXSSLMS)算法,不能够同时满足快速收敛和小稳态失调误差的要求。克服LMS算法的这一缺点需要步长因子在算法初始阶段具有较大值,能够加速收敛,而当算法趋于收敛时具有较小值,以降低稳态失调误差,即采用 变 步 长 因 子 LMS(Variable Step-Size LMS,VSSLMS)算法。为此,针对如何实时改变步长因子大小,研究者们从上世纪90年代开始陆续进行了大量的研究。文献[6]提出了利用算法输出误差均方值迭代更新步长因子的方法,不过该方法受噪声干扰影响较大。文献[7]针对文献[6]的不足,提出利用当前与前一时刻输出误差的相关改变步长因子的方法,该方法具有快的收敛速度和小的稳态失调误差,较好地解决了白噪声干扰的问题。文献[8]在Sigmoid函数(又称Logistic函数)基础上,建立了步长因子与误差信号之间一种新的非线性函数关系,该方法克服了S函数变步长LMS算法在收敛状态下步长因子较大的缺陷,文献[9]利用双曲正切函数建立了步长因子与误差信号间的非线性关系,文献[10]提出了基于最小加权系数均方误差的变步长方法,不过这 3种方法都存在易受噪声干扰影响的问题。文献[11]针对归一化LMS算法(Normalized LMS, NLMS)提出了一种变步长方法,不过该方法增加了计算复杂度,不易实现。文献[12]在分析文献[10]的基础上,将其中的变步长方法应用于选择部分更新滤波加权系数的LMS算法,既达到了快速收敛的目的,又减小了算法的计算量。文献[13]从理论上总结了已有几种VSSLMS算法,并分析了这些算法在不同噪声干扰背景下的稳态性能,文献[14]分析了LMS算法在循环平稳高斯白噪声输入下的性能。
综上所述,已有VSSLMS算法均是基于算法输出误差调整步长因子的大小,易受噪声等因素的干扰。针对该问题,本文提出了迭代变步长LMS算法(Iterated Variable Step-Size LMS, IVSSLMS),该方法建立了步长因子与算法迭代次数(即迭代时间)之间的非线性关系,使得算法在初始阶段具有大步长因子,在趋于收敛时步长因子小。该方法不同于现有方法由输出误差控制,所以受噪声干扰影响较小,与已有变步长LMS算法相比,既能够保证收敛速度不低于已有方法,又可使稳态失调误差减小 7 dB以上。
本文后续内容安排如下:第 2节首先叙述了FXSSLMS算法的基本原理,给出了其收敛性和稳态失调误差的现有分析结论;第3节建立步长因子与收敛时间的改进Logistic函数非线性关系,提出了IVSSLMS算法;第4节从理论上推导分析了所提方法的收敛性能、稳态失调误差和计算复杂度;第5节通过与已有几种变步长方法进行仿真对比,验证了本文方法的正确性;最后对论文内容进行了总结展望。
2 定步长LMS算法基本原理及其性能分析
2.1 LMS算法基本原理
LMS算法计算简单、易于实现,在自适应滤波、参数估计和干扰消除等方面都有广泛应用,其模型如图1所示,数学表示为[1]


图1 LMS算法模型
2.2 LMS算法的收敛性和稳态失调误差
由于LMS算法是递推求解的过程[1],故分析其稳态失调误差及收敛性能是必不可少的,是改进算法的基础。根据式(3)所示的加权系数计算过程,可知输入参考信号向量x(n),估计误差e(n)均具随机性,而步长因子μ由算法本身设定,是影响LMS算法收敛速度和稳态失调误差的关键。
文献[1]中对 LMS算法的性能进行了详细的理论分析。由于输入信号自相关矩阵的特征值λi,未知滤波系数w︿i和算法加权滤波系数 wi( 0) 为定值(0 ≤ i ≤ N - 1 ) ,算法的均方误差只与步长因子 μ 和迭代次数n相关。推导得出LMS算法收敛的充分条件是:
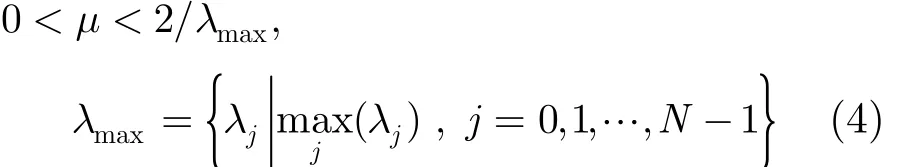
在μ一定的情况下,LMS算法收敛所需迭代次数为

其中,minλ是所有特征值中的最小值,γ为设定的收敛门限值,满足1γ≪。
另外,若LMS算法收敛,则在n→∞时,算法的均方误差(即最小均方误差,MSE)为


由式(4)-式(7)可知,LMS 算法在满足收敛条件γ时所需的迭代次数nγ随步长因子μ的增大(满足收敛条件)而减少,但在n→∞时的稳态失调误差ξ会随μ的增大而增大。所以,在输入信号向量x(n)和噪声信号ε( n)确定情况下,μ是提高LMS算法收敛速度和降低其稳态失调误差的关键。
3 迭代变步长LMS算法
在上一节对LMS算法特点描述的基础上,本节提出步长因子随迭代时间非线性改变的 IVSSLMS算法,既可提高算法收敛速度,又能够降低稳态失调误差。
为解决第2节分析的收敛速度与稳态失调误差相互制约的问题,文献[6-12]提出了多种 VSSLMS算法,使得μ在算法初始阶段具有较大值,随着算法输出误差的减小而逐渐变小,以降低稳态失调误差。
不过,已有的变步长方法容易受外界噪声等干扰的影响。为弥补该不足,本文提出了 IVSSLMS算法,算法中的μ随迭代时间(可等价于迭代次数)增大而逐渐减小,从而避免噪声等干扰的影响。为使步长因子取值满足式(4)所示的收敛条件,且在收敛时具有小的稳态失调误差,对步长因子取值加以限定。再依据改进 Logistic函数建立与迭代次数 n间的非线性关系,如式(9)所示。

其中,μmin是依据式(7)设定的步长因子最小值,μmax是由式(4)和式(5)设定的步长因子最大值,κ是需根据不同情况设定的调整参数,控制了μ(n)随n变换的快慢,m是步长因子改变对应的起始时刻,初始值为0。由式(9)可知μ(n)随n单调递减,变换趋势如图2所示。
VSSLMS算法的滤波加权系数向量递推计算由式(3)变为

图2 步长因子μ(n)变换曲线

为了使本文 IVSSLMS算法具有应对未知滤波器系数︿w突变的能力,步长因子随迭代次数改变的同时,通过对前后时刻输出误差进行功率检测,判断︿w是否发生突变。算法模型如图3所示,基本流程如下:
(1)算法初始,由加权系数向量w(n)的维数N,输入信号功率,噪声功率及设定的最大稳态失调比η,计算参数minμ,maxμ和κ,起始时刻m=0,即迭代次数n由0起始;
(2)由设定参数实时计算每次迭代时的步长因子()nμ,之后执行LMS算法其余部分;
(3)估计当前时刻误差e(n)的功率大小,与前一时刻误差信号(1)e n-比较,若大于设定的门限值χ,则执行步骤(4),小于则直接返回执行步骤(2);
(4)将当前时刻的迭代次数n赋值给m,由当前时刻的信号x(n)的功率估值更新参数minμ,maxμ和κ,返回执行步骤(2)。
其中对不同时刻误差信号的功率估计,计算如式(11)(输入信号同此):
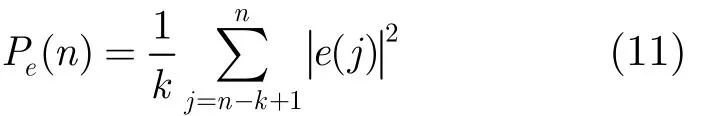
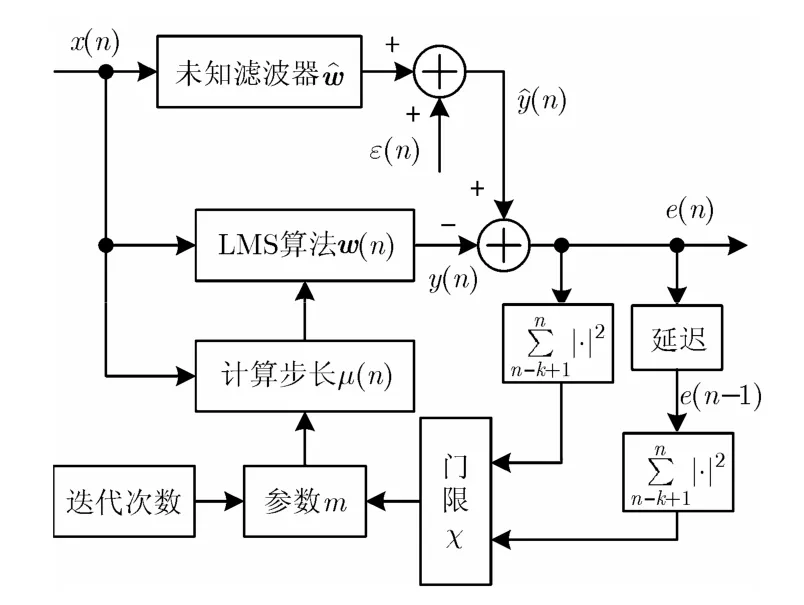
图3 迭代变步长LMS算法原理图
4 算法性能分析
本节将在上一节介绍原理基础上,推导本文算法的收敛速度和稳态失调误差,分析该算法的计算复杂度,并与FXSSLMS和已有VSSLMS算法进行对比分析,同时给出了算法中参数minμ,maxμ和κ的取值准则。为简便起见,本节的分析均以实信号为例,矩阵的共轭转置与转置等价。
4.1 收敛性和稳态失调误差分析
算法的输入信号向量x(n)和估计误差e(n)均具随机性,假设参考信号 x(n)是均值为 0,功率为 P的随机信号,ˆy( n)是x(n)滤波后与噪声ε(n) 的叠加信号,即 ˆy ( n ) =x(n ) + ε(n) 。其中, ε(n) 是均值为0、方差为的高斯白噪声,为未知的滤波器系数,=…]T。由式(2)可得:


则误差信号的均方值可表示为

由于()nε为高斯白噪声,与信号向量x(n)统计独立,利用直接平均法[1]得

式中, R = E{ x ( n ) xT(n)}是输入信号向量x(n)的统计平均自相关矩阵,为共轭对称矩阵。根据共轭对称矩阵性质,可通过酉矩阵U将R对角化,对角矩阵元素λj为R的特征值,如式(16)所示。

再令 C (n ) = UTc( n) ,则根据式(10)和式(13)可得

由式(16)可得 R =UΛ UT,又因c( n ) =UC ( n),将二者代入式(15),可得

由于输入信号向量x(n)与白噪声()nε统计独立,式(18)可展开为
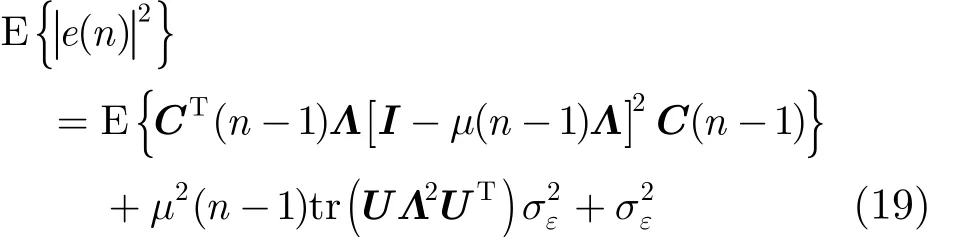
这里tr()⋅表示求矩阵的迹。以此类推,有

其中

由于酉矩阵不改变矩阵的迹,整理得

可等价于

可见式(24)收敛条件为,对于任意的i和j均有1 - μ ( i )λj< 1,与式(4)给出的 LMS算法收敛条件相符。下面根据式(24)-式(26),与 FXSSLMS 算法对比分析本文方法性能。
由上述的分析可知,算法的收敛性取决于式(25)中累积乘积取值的变化趋势,对于FXSSLMS算法μ( i)为恒定值,即本文算法和FXSSLMS算法的收敛因子[1]分别为ρIVSS(n)和ρFXSS(n):

设最大特征 λmax= 1 , FXSSLMS算法的步长因子为 μ =0.1/λmax,本文算法中 μmax=8μ, μmin= 0 .5 μ,则两种算法的理论收敛曲线如图4所示。对于一般信噪比情况,当 ρ (n)< 1 0-20时均可近似为0,由图可见本文算法的收敛速度明显快于FXSSLMS算法。

图4 不同参数对应的收敛因子变化曲线
由迭代变步长因子式(9)可知,μ ( ∞) ≈ μmin,与FXSSLMS算法失调误差式(7)的推导相同[1],本文算法在n→∞时的稳态失调误差为

由参考信号 x(n)功率和阶数 N 可估计出 x(n)自相关矩阵的特征值,进而设定 μmax=0.8/λmax,结合式(29)可得 μmin。根据对信号ˆy( n)的信噪比估计,设定式(5)中的收敛门限值γ,其值应远小于噪信比。为了同时兼顾收敛速度和稳态失调误差,本文算法的参数κ取值应使得收敛因子需小于收敛门限值γ,且步长因子应处于图3中变化速度最快的区域。
4.2 计算复杂度分析
除算法收敛速度和稳态失调误差外,计算复杂度也是影响其应用的重要因素。分析本文IVSSLMS算法的计算复杂度,并与FXSSLMS和文献[7,9-11]中的 VSSLMS算法进行对比。式(9)中指数运算一般采用查表法,可暂等价于1次乘法运算,故本文算法每次计算步长因子需要4次加法,4次乘法和2次除法。由于本文算法除计算步长因子外的递推步骤与FXSSLMS算法相同,若假设算法的滤波器阶数为 N,则由式(1),式(2)和式(10)可得本文算法的其余递推运算共需2N次加法和2N+2次乘法。同理可得 FXSSLMS算法和文献[7,9-11]中 VSSLMS算法一次递推所需的运算量,如表1所示。由表可知,本文算法的运算量略高于FXSSLMS算法,与文献[7]中的 VSSLMS算法相当,小于其他几种VSSLMS算法。可见,本文算法具有低的计算复杂度,便于硬件实现。

表1 不同算法一次递推所需的运算量
5 仿真验证
本节将分别在白噪声和有色噪声干扰下进行仿真,相应结果取 200次独立仿真的平均值,与FXSSLMS算法和文献[7,9-11]中的 4种 VSSLMS算法对比,以验证所提方法的性能。参考文献[7,9-11],仿真时4种VSSLMS算法的相关参数设置如表2所示,其中文献[10]和文献[11]另有调整参数δ和ζ。
5.1 白噪声干扰
白噪声干扰仿真条件设置为:未知滤波阶数N= 5 , 系数[15]w︿ =[0.227, 0.460, 0.688, 0.460,0.227]T,在第 2000个数据滤波系数变为w︿ =[- 0.298, 0.225, 0.849, 0.225,- 0 .298]T;输入信号x(n)为零均值高斯白噪声,方差= 1,即 x(n)平均功率为1;干扰ε(n)为零均值高斯白噪声,其方差为= 0 .0001和= 0 .05 ,即信噪比SNR为40 dB 和 13 dB两种情况。两种信噪比对应的本文算法(IVSSLMS)参数分别为 κ1=85, χ1=和κ2=55, χ2=。由于参考信号不变,所以算法的步长因子取值范围在两种信噪比下相同。为避免步长因子取临界值导致不收敛,令 μmax=0.8/N)=0.16,为减小稳态失调误差令μmin=0.005(/ N )= 0 .001。为使稳态失调比小于0.1,两种信噪比下 FXSSLMS算法的步长因子均为== 0 .04。另外,表2中4种VSSLMS 算法的步长因子取值上下限与本文算法相同,所有算法的滤波加权系数向量初值 w ( 0)=0。两种信噪比对应的仿真结果分别如图5和图6所示。

表2 不同算法对应参数

图5 SNR=40 dB白噪声仿真结果

图6 SNR=13 dB白噪声仿真结果
由图5可见,在高SNR(40 dB)的白噪声背景下文献中4种VSSLMS算法收敛速度和稳态失调误差性能均优于FXSSLMS算法,不过文献[10]和文献[11]中的两种算法跟踪调节能力较弱,这是因为二者的步长因子不能随误差信号的突然增大而迅速变大。文献[9]中算法的性能比较平稳,不过其稳态失调误差与文献[7]相比较大。通过对比可见,本文IVSSLMS算法的收敛速度和稳态失调误差性能均优于已有的4种方法,且具有良好的跟踪能力。由图 6可见,在SNR3 dB较低情况下,几种VSSLMS算法与FXSSLMS算法相比,收敛速度优势不再明显,文献[9,10]中的两种算法收敛速度略慢于FXSSLMS算法,但VSSLMS算法的稳态失调误差均小于FXSSLMS算法。本文IVSSLMS算法在该信噪比下,能够达到的最小稳态失调误差比已有VSSLMS算法降低了3 dB以上。

图7 SNR=40 dB有色噪声仿真结果
5.2 有色噪声干扰
在 5.1节仿真条件基础上,将白色噪声干扰改为有色噪声。有色噪声ε(n)产生是白噪声通过一个一阶系统使前后序列具有相关性[15],1 - 0 .9z-1。同样以信噪比为40 dB和13 dB两种情况进行仿真,其余所有仿真条件和算法参数设置同5.1节。有色噪声下,两种信噪比对应的仿真结果分别如图7和图8所示。

图8 SNR=13 dB有色噪声仿真结果
由图7可见,有色噪声高SNR下,文献[10]的VSSLMS算法性能急剧下降,这是因为具有相关性的噪声对该算法其步长变化影响较大。其余几种VSSLMS算法性能与白噪声下相近。由图8知,当有色噪声条件下SNR减小为13 dB时,文献[7]的算法受影响最大。此时,本文 IVSSLMS算法体现出了更为优越的性能,在保证收敛速度和跟踪能力不低于已有VSSLMS算法前提下,稳态失调误差降低了7 dB以上。
由本节的仿真及分析可知,本文 IVSSLMS算法在不同噪声背景下,均具有快的收敛速度、低的稳态失调误差和良好的跟踪能力,抗干扰能力,尤其是相关噪声干扰,明显优于已有VSSLMS算法。
6 总结
本文在分析了 FXSSLMS算法性能和已有VSSLMS算法特点基础上,提出了迭代变步长LMS算法(IVSSLMS),对其收敛性和稳态失调误差进行了理论分析。该算法通过建立迭代次数与步长因子间的改进 Logistic函数非线性关系,使得算法初始阶段步长因子值较大变化慢,在收敛阶段趋于恒定的最小值,从而获得快的收敛速度和低的稳态失调误差,且不易受噪声等干扰因素的影响。仿真表明,在白噪声条件下,本文 IVSSLMS算法的收敛速度和稳态失调误差性能略优于已有的4种VSSLMS算法,有色噪声下稳态失调误差降低了7 dB。所以,本文所提的迭代变步长 LMS算法具有快的收敛速度,低的稳态失调误差和更强的抗干扰的能力,且变步长方法易于数字硬件实现,具有较高的实际应用价值。
[1] Simon H著. 郑宝玉译. 自适应滤波器原理[M]. 第4版, 北京:电子工业出版社, 2010: 206-212.
[2] Huang Bo-yan, Xiao Ye-gui, Sun Jin-wei, et al.. A variable step-size FXLMS algorithm for narrowband active noise control[J]. IEEE Transactions on Audio, Speech and Language Processing, 2013, 21(2): 301-312.
[3] Xu Ding-jie, Yin Bo, Wang Wei, et al.. Variable tap-length LMS algorithm based on adaptive parameters for TDL structure adaption[J]. IEEE Signal Processing Letters, 2014,21(7): 809-813.
[4] Choi Y S and Hooman S M. Simultaneous transmission and reception: algorithm, design and system level performance[J].IEEE Transactions on Wireless Communications, 2013,12(12): 5992-6010.
[5] Harsha I K R and Behrouz F B. Fast LMS/Newton algorithms for stereophonic acoustic echo cancelation[J].IEEE Transactions on Signal Processing, 2009, 57(8):2919-2930.
[6] Kwong R H and Johnston E W. A variable step size LMS algorithm[J]. IEEE Transactions on Signal Processing, 1992,40(7): 1633-1642.
[7] Aboulnasr T and Mayyas K. A robust variable step-size LMS-type algorithm: analysis and simulations[J]. IEEE Transactions on Signal Processing, 1997, 45(3): 631-639.
[8] 罗小东, 贾振红, 王强. 一种新的变步长LMS 自适应滤波算法[J]. 电子学报, 2006, 34(6): 1123-1126.Luo Xiao-dong, Jia Zhen-hong, and Wang Qiang. A new variable step size LMS adaptive filtering algorithm[J]. Acta Electronica Sinica, 2006, 34(6): 1123-1126.
[9] 田福庆, 罗荣, 李克玉, 等. 基于改进的双曲正切函数变步长LMS算法[J]. 系统工程与电子技术, 2012, 34(9): 1758-1763.Tian Fu-qing, Luo Rong, Li Ke-yu, et al.. New variable step-size LMS algorithm based on modified hyperbolic tangent function[J]. Systems Engineering and Electronics,2012, 34(9): 1758-1763.
[10] Mayyas K and Momani F. An LMS adaptive algorithm with a new step-size control equation[J]. Journal of the Frankin Institute, 2011, 348(4): 589-605.
[11] Huang Hsu-chang and Lee Jung-hsi. A new variable step-size NLMS algorithm and its performance analysis[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 2055-2060.
[12] Mayyas K. A variable step-size selective partial update LMS algorithm[J]. Digital Signal Processing, 2013, 23(1): 75-85.
[13] Zhang Sheng and Zhang Jia-shu. New steady-state analysis results of variable step-size LMS algorithm with different noise distributions[J]. IEEE Signal Processing Letters, 2014,21(6): 653-657.
[14] Bershad N J, Eweda E, and Bermudez José C M. Stochastic analysis of the LMS and NLMS algorithms for cyclostationary white gaussian inputs[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2238-2249.
[15] Hwang Jeng-kuang and Li Yuan-ping. Variable step-size LMS algorithm with a gradient-based weighted average[J].IEEE Signal Processing Letters, 2009, 16(12): 1043-1046.

