SHPB在节理岩石动力学性能分析中的可行性研究

李业学，徐福卫



SHPB在节理岩石动力学性能分析中的可行性研究

李业学1,2，徐福卫1

(1.湖北文理学院建筑工程学院，湖北襄阳441053；2.低维光电材料与器件湖北省重点实验室，湖北襄阳441053)

探讨采用SHPB试验技术分析节理岩石动力学性能的可行性. 通过节理岩石的冲击压缩试验，分析该试验中产生的相对误差对节理岩石应力和能量耗散结论的影响，剖析产生误差的根本原因，并在此基础上提出用12×1黄铜片作为波形整形器将震荡较大的矩形波整形为震荡较小的三角形波的改进方案，试样应力相对误差的试验验证显示46个试样的应力相对误差均在0.5%以下，表明整形后的三角形波或半正弦波分析节理岩石冲击应力是可行的. 研究显示应力波中高频成分的消除和波类型的减少是弥散效应降低的根本原因. 另外，当采用SHPB技术探讨节理岩石的能量耗散问题时，试验只要求在杆中传播的应力波处于一维状态，节理岩石处于一维还是多维应力状态对能耗值没有影响，尽管它的确处于三维应力状态. 这为SHPB试验技术开辟了一条简单可行的应用新途径.

SHPB试验技术；节理岩石；一维应力波假定

SHPB试验技术[1-2]基于一个非常重要的假定和前提，即一维假定[3]. 在该技术提出之初，由于人们试验采用的杆径较小，试验对象多为均质延性材料，其一维假定通常能够得到满足. 但随着SHPB的广泛应用，学者们逐渐发现，理论计算结果与SHPB试验结果相差甚远，甚至出现不可接受的偏差[4]，这是因为在现有试验条件下Poisson效应引发的横向弥散使研究对象处于二维应力状态，SHPB试验技术的一维假定无法满足. 为此，Rayleigh在1984年从理论上探讨了横行弥散效应后研究对象的真实应力，并给出了其应力和波速的解析解[5]. 从其研究成果可知，只要保证恒定应变率或长径比达到一定要求，都可以满足或近似满足一维假定. 于是在随后研究中，学者们通过满足长径比要求，完成了金属、岩石及复合材料的动力学特性研究，探讨了材料的本构关系或能量耗散规律，并取得了丰硕研究成果[6-7]. 在岩石材料研究过程，考虑到岩体富含节理，且在矿业开采、地下厂房开挖等项目中，其动力学特性直接影响到整个结构体安全，所以，节理岩石的动力学特性问题提上研究日程. 文献[8]揭示了表面粗糙度对应力波透反射的影响规律. 通过节理岩石SHPB试验，文献[9]探讨了表面分形维数对应力波能量耗散的影响规律，建立了能量耗散与分形维数之间的定量关系. 以上研究并没有考虑SHPB试验技术对节理岩石试样的适用性. 因而，文献[10]通过动力平衡分析，定性探讨了采用该设备的可行性. 然而，从定性分析上升至定量探讨是研究的必然趋势. 所以，本文拟通过两条节理岩石SHPB试验，定量探讨节理岩石SHPB试验在测定试样应力和能量耗散的可行性，并提出减弱或消除弥散的可行应对措施和解决方案，剖析方案减弱弥散效益的原因和机理.

1 SHPB试验设备及试样

SHPB试验设备本试验采用中国科学技术大学冲击动力学实验室研制的直锥变截面SHPB装置(如图1、2)，该套装置主要包括储存高压气体的氮气瓶，实施冲击加载的子弹，量测子弹冲击速度的激光测速仪，作为应力波传播介质的入射杆和透射杆，吸收能量的吸收杆以及保护设备的阻尼器. 本试验透射杆采用直径为50mm的圆柱形钢杆，杆长1.4m；子弹长200mm，直径37mm；由于子弹与入射杆的直径不一致，为了减小惯性弥散引发二维应力效应，最大限度降低试验系统误差，入射杆采用直锥变截面杆，子弹/入射杆端杆径37mm，入射杆/试样端杆径50mm，杆全长2.4m. 在入射杆和透射杆上分别贴电阻应变片，两应变片分别距各自杆端800mm和350mm，见图1.

试样加工利用标准钻具从岩块钻取大理岩圆柱体岩芯，直径50mm、长80mm. 初步打磨岩石两端面后，将岩芯分别切成含两条倾角各自为(10o、20o、25o)的倾斜节理面，随后沿纵横方向在半成品岩样节理面上随机刻划，使表面粗糙不平，模拟天然状态下的粗糙节理面. 用AB胶水将三节粘合起来. 打磨试样端面直至到达预定长度和其他试验精度要求，最终加工成的成品岩样长度65mm、直径50mm(如图3)，共计46个.

图1 SHPB设备

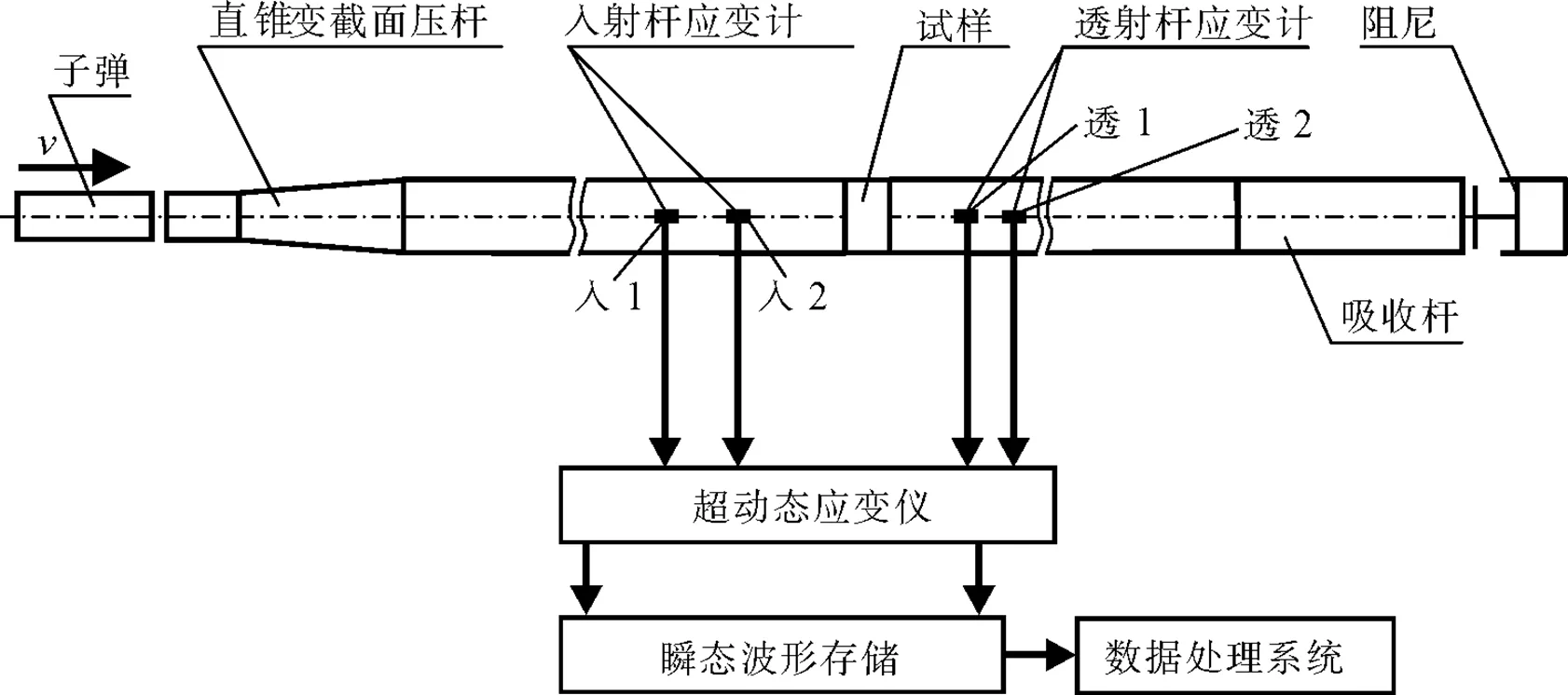
图2 50φ直锥变截面SHPB实验设备结构

图3 岩样成品

2 横向惯性弥散效应分析

2.1 试样应力相对误差分析原理

SHPB试验的所有原理推导均基于两个基本假定：1) 应力(应变)均匀化假定，即应力波在很短时间内经过9～10次反射后试样两端面应力达到一致；2) 测试杆中的应力处于一维应力状态. 然而，在试验中，由于Poisson效应必定同时产生横向变形，应力状态实际上不是简单的一维状态，原来的平截面不再保持平面，严格地说杆处于三维应力状态，至少也是一个轴对称(圆柱体)的二维问题，即产生惯性弥散效应. Pochhammer很早就在理论上探讨了这一问题，从一无限正弦波列沿圆柱体传播出发，通过波动方程和严格的数学推导，得出波的相速C为：

式(1)中，0为一维纵波波速，为波长，为泊松比，为圆柱体半径. 1957年Richard也对此做了严格的数学证明[11]，认为试样的实际应力应该是在一维应力状态下的结论上叠加一个惯性弥散修正项，即：

式(2)中，1，2为试样两端面应力；r试样半径；ρ为试样密度；为试样的应变加速度；L试样长度. 显然，若试验能实现常应变率，则修正项为零，但试验中实现常应变率通常很难控制，可行做法是通过控制试样的长径比，使长径比满足：

2.2 波形整形前试样应力误差分析

由于本试验试样预制两条贯通节理的需要，试样必须具有一定长度，所以试样长径比将与式(3)要求存在一定偏差. 为了弄清试验偏差可能造成的影响，本文依据式(2)计算了试样BB2、CC2、CC4、DA1的应力相对误差. 从图4可以看出，在对应力波整形前，4个试样的误差分别为1.13%、1.34%、7.56%、4.28%，其中CC4误差最大，为7.56％. 显然，如果探讨其本构关系，误差很可能影响分析的精度和试验结论的可信度.

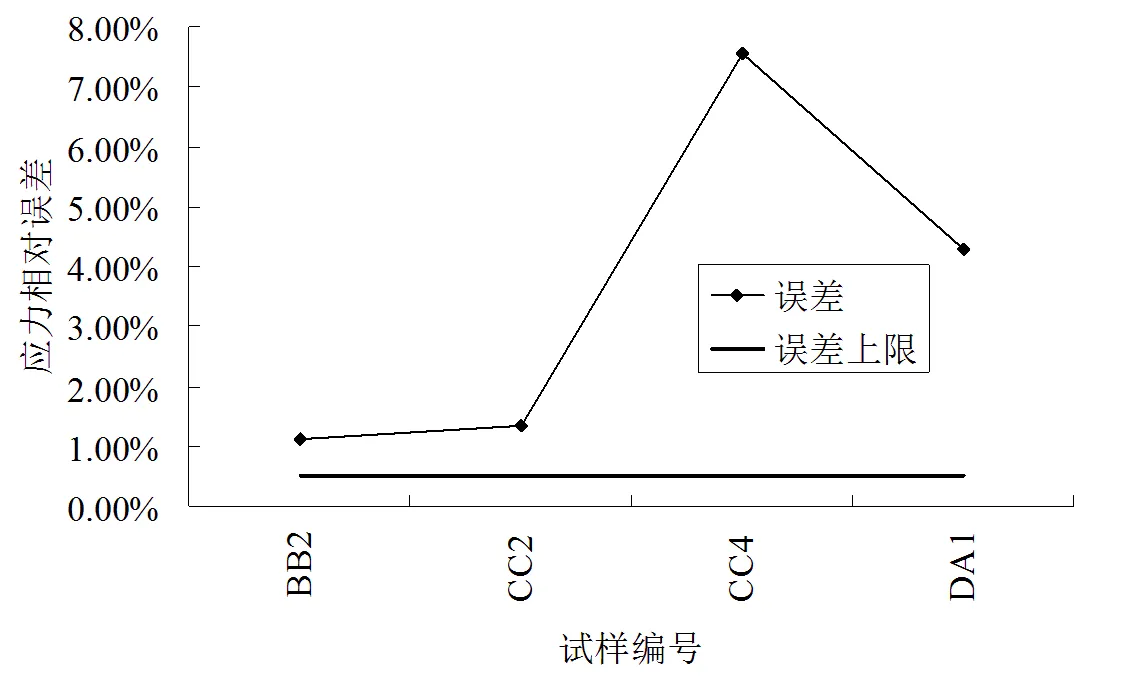
图4 试样误差曲线

这是因为：1)采用傅里叶变换，任何线弹性波都可以分解为多个谐波的叠加. 即一个线弹性波包含了多个频率的谐波，这些谐波按照各自速度向前传播，并随之分散和发生弥散，造成SHPB试验技术的第一个假定(一维波假定)不能满足或满足近似度低. 2)圆柱形子弹加载产生的波形为近似矩形波，矩形波上升沿很陡. 即试件应力从0到达峰值时间很短(理想矩形波不需要考虑时间)，瞬间到达峰值，甚至超过其动态强度，会很快造成材料破坏. 特别是含节理的脆性岩石材料，出现上述现象概率更大. 在节理岩石破坏前，应力波没有充分时间在岩石中发生至少3~4来回反射，以平衡两端面应力，导致SHPB试验的第二个假定即应力均匀假定不能满足. 当然，在不符合试验假定前提下计算的结果当然会存在较大偏差.

2.3 波形整形及试样应力误差分析

2.3.1波形整形技术

为了消除或降低上述偏差，本文采用波形整形技术，即在入射杆杆端加装一个12×1的黄铜片作为整形器，减缓波形上升沿，延长应力达到峰值时间，将波形由矩形波整形为近似三角形波或半正弦波.

图5 试样AA3应变波形

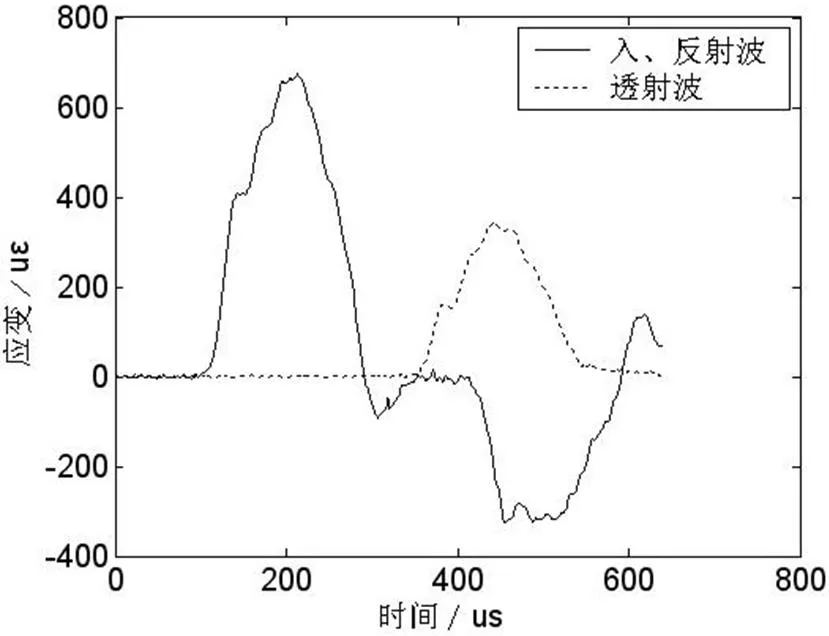
图6 试样AA4应变波形

2.3.2整形后试样应力相对误差分析

图5、6分别给出了整形后试样AA3、AA4的应变波形图. 采用公式(2)，基于Matlab软件编制计算程序，分析从AA1到DD6等剩余46个试样的应力相对误差(见表1)，并绘制各个试样的误差变化图(见图6).

表1波形整形后试样应力相对误差

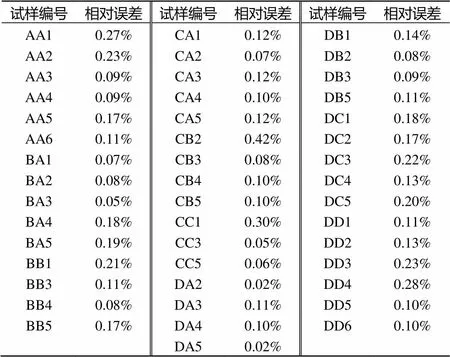
试样编号相对误差试样编号相对误差试样编号相对误差 AA10.27%CA10.12%DB10.14% AA20.23%CA20.07%DB20.08% AA30.09%CA30.12%DB30.09% AA40.09%CA40.10%DB50.11% AA50.17%CA50.12%DC10.18% AA60.11%CB20.42%DC20.17% BA10.07%CB30.08%DC30.22% BA20.08%CB40.10%DC40.13% BA30.05%CB50.10%DC50.20% BA40.18%CC10.30%DD10.11% BA50.19%CC30.05%DD20.13% BB10.21%CC50.06%DD30.23% BB30.11%DA20.02%DD40.28% BB40.08%DA30.11%DD50.10% BB50.17%DA40.10%DD60.10% DA50.02%

分析图7可知，在进行波形整形后，CB2试样产生了最大的应力误差，不过也仅为0.42%，不超过0.5%，且最小误差已达0.02%，分别对应DA2和DA5. 显然，整形技术使得应力误差大幅度减小. 因而，在分析节理岩石的本构关系和应力状态中，其精度能满足分析要求，表明该方法是合理可行的.

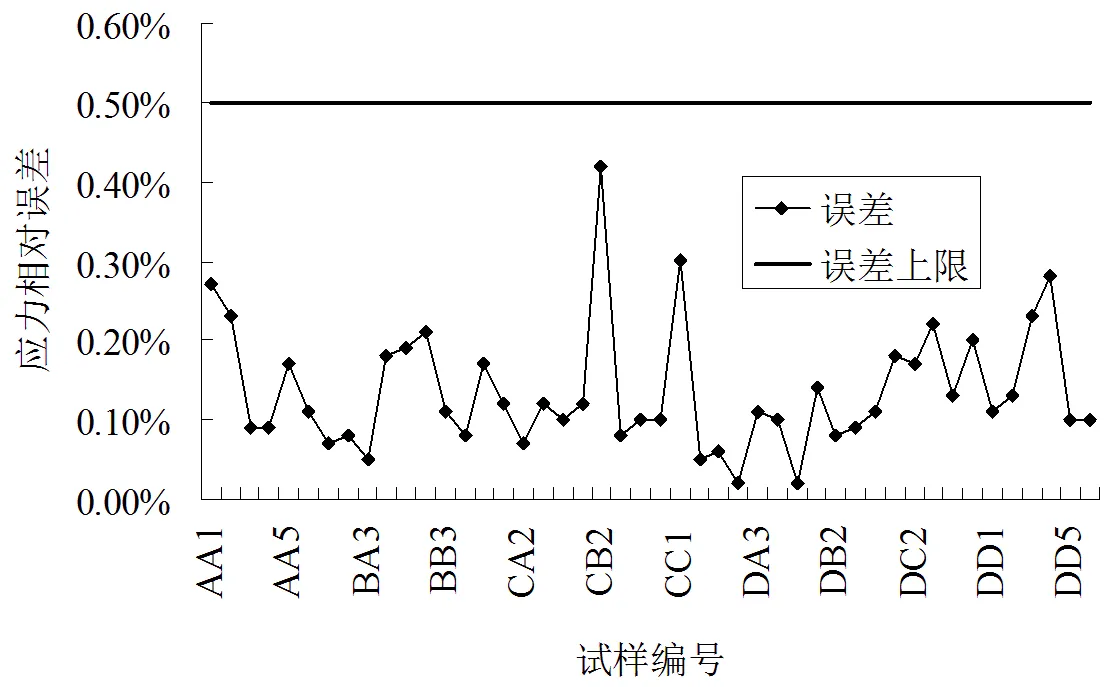
图7 整形后的误差

整形后的波形能有效改善惯性弥散效益产生的负面影响，原因有两个方面：1)通过波形整形，波形由初始的矩形波整形为近似三角形波或半正弦波，减少或消除了矩形波中的高频部分，减小发生弥散效应发生的概率. 2)线性波可分解为多个谐波的组合. 将矩形波整形为近似三角形波或正弦波，实际上减少了其中谐波的成分总数，如果能整形为理想化的半正弦波，则分解后的谐波只包含一种频率的波，在传播过程则不可能发生波的弥散. 当然，如果只整形为三角形，至少被分解后其中的谐波种类减少，这无疑将降低波发生弥散的程度.

另外，当利用SHPB装置分析节理对应力波传播影响规律时，依据能量转化和守恒定律可知，节理引发的能量耗散值可按下式计算

式(4)表明，通过弹性杆中入射波、反射波和透射波的函数表达式或数值信号，可以求解其能耗值. 试件整体就如一个黑匣子，入射杆的入射能量减去其反射能量和透射能量，即为节理岩石的能量耗散值. 因而，试验可以忽略节理试件的应力状态，尽管节理处透反射使得节理岩石处于三维应力状态.

但值得注意的是：在杆中传播的应力波必须保持一维状态，一维应力状态下杆表面应变计测量的轴向应变才可以代表整个截面各点的轴向应变，无畸变的弹性波条件下才可以认为杆中应变计位置测量的应变与试样端面完全一样，即测量位置的受力状态与试样端面完全一样.

从上述分析可知，通过相对简单的约束条件和假定——杆中传播的为一维波，可从另一角度——节理岩石能量耗散来分析节理岩石的动力学特性，为SHPB试验技术开辟了一条新的应用渠道.

3 结论

本文基于SHPB试验技术，通过波形整形前后两类波形对节理岩石脆性材料应力和能耗的影响对比，以及弥散效应对节理岩石应力和能耗的影响分析，揭示弥散效应改善的原因. 主要研究结论包括：

1)圆柱形子弹冲击产生的矩形波震荡较大，惯性弥散效益明显. 在节理岩石冲击压缩试验中，计算出的节理岩石应力误差较大，对节理岩石本构关系分析影响显著，其结果偏差甚至近乎到达错误程度. 采用黄铜作为波形整形器，整形后的三角形波上升沿变缓，对分析岩石等强度较低的脆性材料特别是含节理岩石材料效果明显. SHPB用于节理岩石动力学性能分析是可行的.

2)SHPB用于分析节理岩石的能量耗散问题时，不同于其本构关系的探讨，可忽略节理岩石试样所处应力状态，仅要求杆中传播的应力波处于一维状态即可. 能有效简化节理岩石能耗问题分析的步骤和方案，开辟SHPB试验技术应用的另一领域.

3)当矩形波整形为三角形波或半正弦波后，弥散效应改善的原因是：整形剔除了波中高频成分，并减少了波的种类，不仅降低应力波发生弥散的概率，且减小了波发生弥散的严重程度.

[1] HOPKINSON B. The effects of monetary stresses in metals[J]. Proceedings of the Royal Society, 1905, 74: 498-506.

[2] DAVIES R M. A critical study of the Hopkinson pressure bar[J]. Phil. Trans. A, 1948(240): 375-457.

[3] 王礼立. 应力波基础[M]. 2版. 北京: 国防工业出版社, 2005.

[4] 刘孝敏, 胡时胜. 大直径SHPB 弥散效应的二维数值分析[J]. 实验力学, 2000, 15(4): 371-376.

[5] RAYLEIGH LORD. Theory of Sound[M]. London: Macmil lan Co., 1894.

[6] 单仁亮, 陈石林, 李宝强. 花岗岩单轴冲击全程本构特性的实验研究[J]. 爆炸与冲击, 2000, 20(1): 32-38.

[7] 李业学, 刘建锋, 秦 丽. 应力波穿越岩石节理时能量耗散规律的实验研究[J]. 实验力学, 2011, 26(1): 84-89.

[8] LI YEXUE, ZHU ZHEMING. Study on the velocity of P waves across a single joint based on fractal and damage theory[J]. Engineering Geology, 2012, 151(29): 82 -88.

[9] JU Y, SUDAK L, XIE H. Study on stress wave propagation in fractured rocks with fractal joint surfaces[J]. Int. J. Solids Struct. 2007, 44(13): 4256–4271.

[10] 满 轲, 周宏伟. SHPB系统的动态力平衡分析[J]. 金属矿山, 2010(11): 27-30.

[11] ANTON RICHARD J, SUBHASH GHATU. Dynamic vickers indentation of brittle material[J]. Wear, 2000, 239(1): 27-35.

Feasibility of SHPB Experimental Technique Applied to Analyzing Dynamic Characteristic of Jointed Rock

LI Yexue1,2，XU Fuwei1

(1.School of Civil Engineering and Architecture, Hubei University of Arts and Science, Xiangyang 441053, China; 2.Hubei Key Laboratory of Low Dimensional Optoelectronic Material and Devices, Xiangyang 441053, China)

It discusses the feasibility of SHPB experimental technique applied to analyzing dynamic characteristic of jointed rock. Based on the shock compression test of jointed rock, it analyzes the influence from relative error in the test on the stress and energy dissipation of jointed rock stress, and the reasons for errors as well. Besides, it changed the rectangular wave with big shock to the triangular wave with small shock via a brass slice with a dimension of 12×1. It shows that stress relative error of 46 specimens is less than 0.5%, which indicates that reshaped triangular wave used to analyze shock stress of the rock is reasonable. Moreover, it shows that, the essential reason why diffusion effect reduces is that high frequency components in stress wave are cleared and the numbers of wave type are decreased. In addition, when SHPB experimental technique is employed to investigate energy dissipation of jointed rock, in the experiment one dimensional stress wave propagating in the bar must be satisfied. Whether the jointed rock is in one dimensional stress state or in multidimensional stress state is not influential on energy dissipation, although it is indeed in three-dimensional stress state. It finds out a new simple feasible application field for SHPB experimental technique.

SHPB experimental technique; Jointed rock; One dimensional stress wave hypotheses

(责任编辑：饶 超)

TU458+.3

A

2095-4476(2015)08-0036-05

2015-03-12;

2015-04-15

湖北省教育厅科学技术研究计划重点项目(D20142603)

李业学(1977— ), 男, 湖北荆州人, 湖北文理学院建筑工程学院副教授, 博士, 主要研究方向: 材料动力学.