基于课标课程的中学数学建模教学的实践研究
范翠华
摘 要:新课程标准将“数学建模”“数学探究”等纳入数学研究性学习的形式当中,倡导对学生数学学习方式的丰富以及独立思考、自主探索、动手实践等能力的培养,明确规定了中学数学课程需在向学生提供基本内容的同时反映数学的应用性,积极展开数学建模活动。在分析中学数学建模主要原则和具体步骤的基础上,针对不同类型的数学模型展开建模教学的实践研究,以期为当下中学数学的建模教学提供参考。
关键词:课标课程;中学数学;模型
一、中学数学建模的主要原则
1.趣味性
在中学数学课程中引入数学建模是为了使中学生真正体验到生活中数学的重要作用,激发学生主动接触、学习数学的兴趣。因此,教师需立足于满足学生爱好、贴近实际生活且符合学生现有数学知识结构的前提下进行建模问题的选择,通过富有趣味与挑战性的问题的设置来调动学生的积极性,进而主动参与到建模教学活动中。
2.可行性
由于教学的接受者是中学生,故建模问题的选取必须适合中学的数学知识水平,并在不同阶段的建模训练中结合教学现实选取相应的问题,做好由易到难、由简及繁的过渡。
3.发展性
建模问题的选用首先应当渗透中学生数学的数学思想方法,让学生在建模学习过程中巩固并内化所学知识,得到进一步发展。建模问题的解决并非是建模教学的最终目标,需强调问题解决后所带来的延伸作用。
二、中学数学建模的具体流程
作为一种创造性数学思维活动,数学建模的模式、方法并非是固定的,但总结起来大致包括以下几个流程。
1.准备
建模准备环节要在分析问题实际背景的基础上做好数据、资料的收集与整理,发现问题的内在联系并对其中所涉及的量的关系做出分析。
2.假设
从建模目的和实际问题特征出发对问题进行有选择性、必要性的简化,并针对题目条件进行有选择的理想化,经抽象思维思考后使用数学语言对问题提出假设,合理选择变量。
3.建模
使用相应的数学方法根据假设建立不同变量间的关系模型。
4.求解
计算所建立的数学模型并进行求解证明。
5.分析
数学分析建模的求解结果,例如变量间关系、最优解或最优决策,此外还可对所得结果做出进一步的预测。
6.检验
在实际问题中代入分析结果以实现对求解结果合理性、真实性、科学性、可行性的检验,在必要的情况下可修正模型,通过再计算—再检验—再修正的反复循环得到最理想的结果。
三、基于课标课程的中学数学建模教学实践路径
1.降低难度,树立信心
在建模教学的初级阶段需尽量多地选用一些易于寻找模型的题目,让学生在获得成功体验的过程当中逐步形成建模的自信心。对于现实生活中普遍存在的增长率、浓度配比、存款利息等可利用方程这一较为简单的数学模型来表达数量间的相等关系。例如,在讲解七年级方程的相关内容时,教师可先设计这样一个问题:
例1:一件衣服的售价是132元,在降价进行9折出售的情况下,相比较进价仍然可获得10%的利润,求衣服的进价是多少?
假设衣服进价是x元,那么根据问题可列出132×0.9-x=10%x这一方程,并解得x为108。
学生通过这个简单方程式求解的平台获得了成功的体验,而后教师可在此基础上进行深化。
例2:某工厂甲车间与乙车间年度计划总共完成720万元的税利,结果甲、乙车间分别完成了计划的110%和115%,共计完成812万元的税利,那么甲、乙车间分别超额完成了多少万元的税利?
在分析问题后可应用x+y=max+by=n这一模式,假设甲乙两车间完成的税利分别是x、y万元,那么可得出方程式组x+y=720110%x+115%y=812,解得x=320,y=400。进而由320×10%和400×15%得出甲、乙车间分别超额完成了32万元与60万元的税利。
这样由易到难逐级递进的教学方法能够帮助学生打好基础,同时贴近实际生活的问题选择也让学生了解到了数学建模的无处不在,初步形成了建模意识。
2.发散思维,开拓思路
例3:根据一次函数y=6x+12设计不同的问题,学生在讨论与思考后编写出了各种不同的生活背景。
1.出租车的起步价是12元,若超出规定公里数后需每公里增加6元,假设超出x公里,出租车费为y元,则两者的函数关系是y=6x+12。
2.公园里的一个花坛长6 m,宽2 m,现在要保持花坛的长度不变,宽度增加x(m)来扩大花坛的面积,那么扩大后的花坛面积y(m2)和x(m)的关系式是y=6x+12。
3.弹簧长12 cm,每挂上一个重1 kg的物体便增长6 cm,那么弹簧的长度y(cm)和物体重量x(kg)之间的关系是y=6x+12。
在自己编写题目后学生对建模思路有了更清晰的把握,并且学会了多角度、多方位地思考数学问题,有利于培养学生建模的灵活性。
3.绘制图表,加深理解
建模过程中准确理解与把握题目的含义是至关重要的。中学生的思维发展相对来说还不够成熟,往往在阅读文字时很难形成直观形象的概念。因此,中学教师在建模教学中必须指导学生掌握理解问题的方法,可引导学生通过绘制表格或图像等来直观地分析问题。
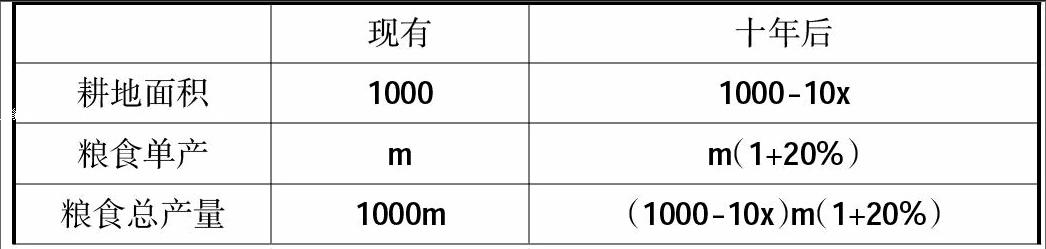
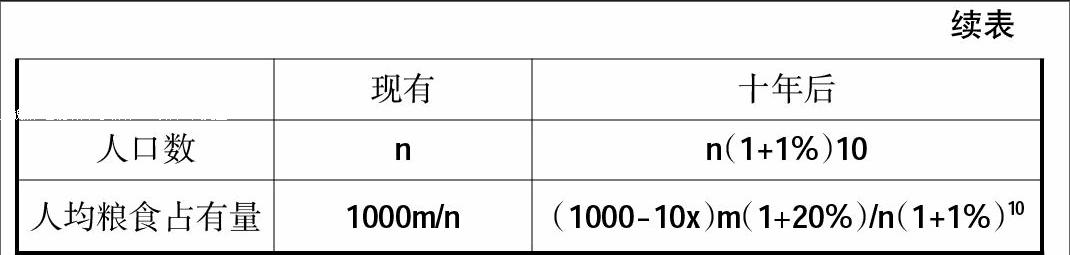
例4:某地区已有1000公顷耕地,计划在十年后粮食单产比现在增加20%并且人均粮食占有量相比较现在提升15%。若人口的年增长率是1%,求耕地每年最多只能减少多少。
该题目中的数量关系复杂,涉及现有的及十年后的耕地面积、人口、粮食单产等诸多数量,此时教师便可引导学生绘制表格整理数据。如下:
经过列表梳理后学生可以从复杂的数量关系当中准确、清晰地找出关联数量,理解题意后便能够很容易地建立数量关系模
型了。
四、总结与建议
在中学数学的建模教学过程中,教师需结合建模基本原则和学生实际情况适当选择建模切入点。在建模教学初期,考虑到中学生在建模初级阶段经验不足、意识薄弱,因此需密切结合教材选用一些较为简单的建模问题,以指导学生了解、构造模型为目的,帮助学生消除对数学建模的畏难心理;在建模教学中期,可着重培养学生提取信息、应用信息的能力;而在建模教学后期,可鼓励学生自主搜集建模信息、数据并进行假设建模,从而逐步、有效地培养中学生的数学建模能力与数学知识应用能力。
参考文献:
张晓晖.基于建构主义的中学数学建模教学研究[D].山东师范大学,2012.

