不等式恒成立问题“三步走”策略
冯刚
江苏卷考试说明中《不等式》一章有两个C级要求,一是基本不等式,二是一元二次不等式,并未提及对“不等式恒成立问题”的要求,而新高考中2008年第14题、2011年第19题,2014年第10题和第19题都涉及处理恒成立问题,平时各大市的模考卷中解决此问题的也有很多,而且要求较高,难度大。因此,笔者结合一线教学经验,归纳此类问题的“三步走”策略。
第一步策略:常规思路
(一)可分一般的恒成立和特殊的恒成立两类
1.一般的恒成立问题可由三步解决:
例1.已知函数f(x)=2x.
(Ⅰ)求函数F(x)=f(x)+af(2x),x∈(-∞,0]的最大值;
(Ⅱ)若存在x∈(-∞,0),使f(2x)-af(x)>1成立,求a的取值范围;
(Ⅲ)若当x∈[0,3]时,不等式f(x+1)≤f[(2x+a)2]恒成立,求a的取值范围.
(Ⅰ)(Ⅱ)略
(Ⅲ)分析:对于恒成立问题,第一步是认清自变量和参数,可与解不等式问题对比理解。解关于x的不等式x2-2ax+(a2-1)≤0问题过程为[x-(a-1)][x-(a+1)]≤0,即(a-1)≤x≤(a+1)。感受到a为参数,x是自变量,即解不等式求的是自变量的范围。而恒成立问题已知的是自变量的范围,求的是参数的范围。如果没认清,可能会产生问题(见例2);第二步是看能否分离参数,再根据示意图找等价条件;第三步就是研究等价条件中的最值问题。
2.特殊的恒成立一般有两种情况:
(1)一次在闭区间上恒成立
例2.若不等式kx2-2x+1-k<0对满足-2≤k≤2的所有k都成立,求x的取值范围.
分析:如果按一般恒成立步骤,先认清自变量和参数,k为自变量,x为参数,然后讨论分离参数,再找等价条件,较烦。
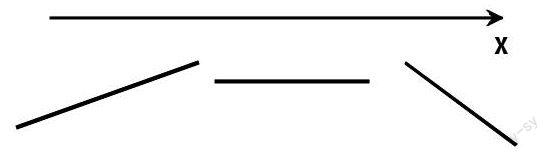
再深入分析,由于f(k)=kx2-2x+1-k为一次函数,图象是一条直线,无论这个图象是单调增,还是与x轴平行或重合,只要保证两端都小于0,那在闭区间上的所有函数值都小于0,甚至图象是单调减时也只要保证两端都小于0(如示意图),因此,可以直接写出等价条件f(-2)<0f(2)<0。因此对于一次在闭区间上的恒成立这种特殊情况,只需要将闭区间两端点值代入不等式即可。
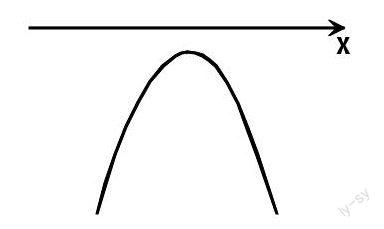
(2)二次在R上恒成立
由此可见,对于二次在R上恒成立的这种特殊情况,只需根据图象利用Δ解决。
(二)针对用常规思路解决的恒成立问题,一般可能考查五个难点
1.可能难在对不等式的处理。
2.可能难在认清自变量和参数,如例2,若分不清,可能看成关于x的二次不等式。
3.可能难在能不能分离参数,如例1,明显是方法一分离参数法简单,原因是如果能分离参数,那第三步研究最值的函数就是不含参数的函数,若不分离,那第三步研究最值的函数就是含参的函数,因此能分离参数最好要分离参数。
4.可能难在最值问题的处理,如例1,方法二要研究的是含有参数的二次函数在区间上的最值。
5.可能难在等价条件的“修正”。
第二步策略:应用恒成立条件,缩小参数范围
例4.若不等式(mx-1)[3m2-(x+1)m-1]≥0對于任意m∈(0,+∞)恒成立,则实数x的值是 .
分析:如果按第一步策略即常规方法,一是不大可能分离参数,二是不分离参数时要研究的函数的最值又很难求。此时可由“解决恒成立问题”的思路调整为“恒成立是条件”,因此,可取m∈(0,+∞)上的一个值代入不等式从而来缩小a的范围,可能对分离参数有帮助。本题若取m=1,可得(x-1)2≤0?圯x=1。当然这里比较特殊,取值代入后可直接求出参数的值,有时可能没这样特殊,求不出值,但此策略也可缩小参数的范围,从而为分离参数法做好准备。
第三步策略:数形结合
例5.已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是 .
例6.设f(x)=4x3+mx2+(m-3)x+n(m,n∈R)在[0,1]上是单调减函数,则m的取值范围为 .
分析:此题先可转化为f′(x)=12x2+2mx2+(x-3)≤0对于x∈[0,1]恒成立,前两策略处理较烦,根据f′(x)示意图,等价条件为f′(0)≤0f′(1)≤0?圯m≤-3。

