利用微软Math3.0设计教学《函数y=Asin(ωx+φ)的图像》
李晶

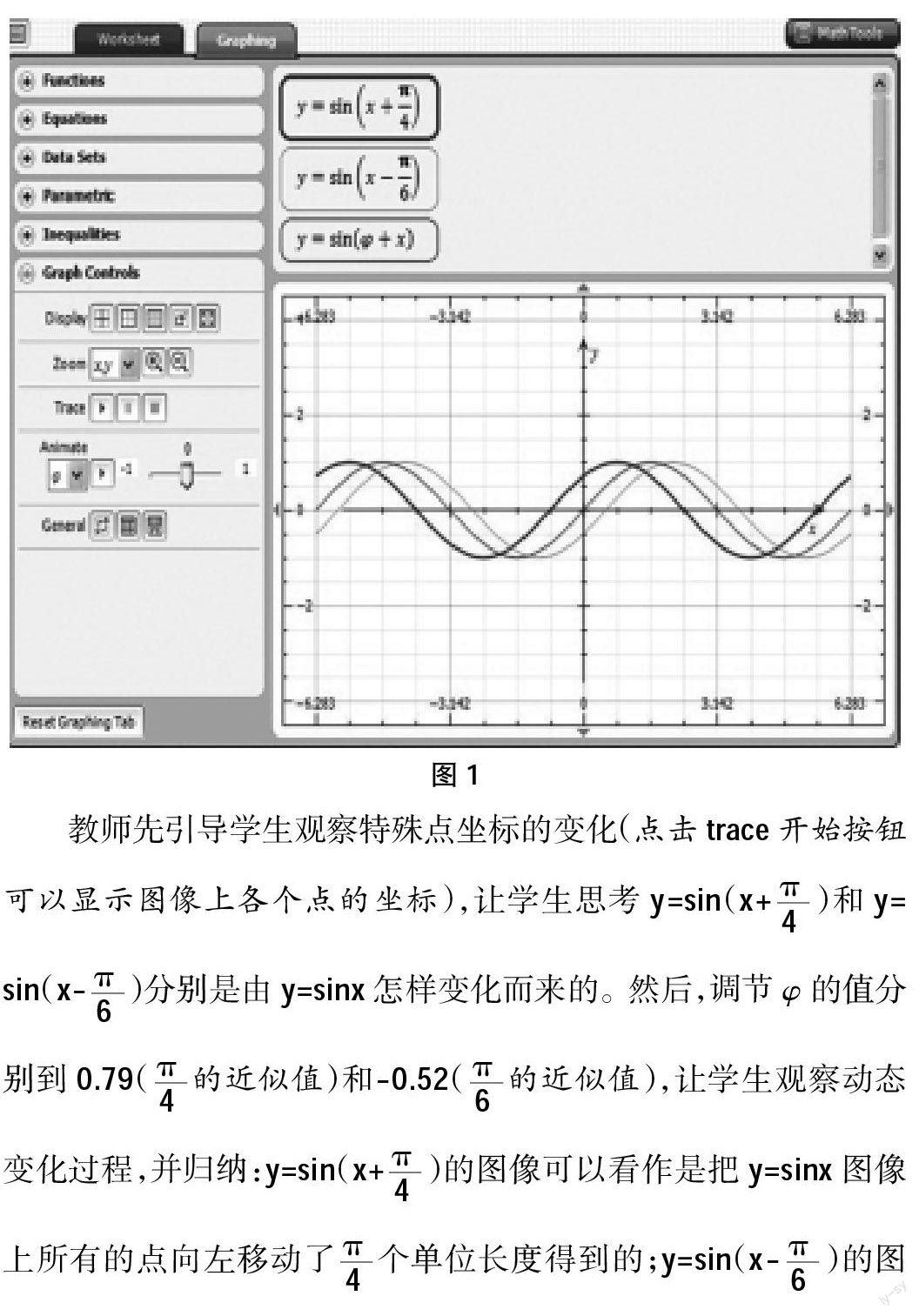
函数y=Asin(ωx+φ)是三角函数一章中的重點和难点。这节课如果只采用传统的板书教学,不仅作图量大,而且要在同一坐标系中作出多个精确的图像比较困难,不利于引导学生从感性认知快速准确地上升为理性认知。为了提高课堂效率,一些老师采用几何画板辅助教学,变静为动,变抽象为直观,这样比单纯板书作图效果好,容易突破学生理解上的难关。但是,在实际教学中,很多教师并没有采取这种先进的手段,除了教学观念、态度等的原因外,有一个关键原因是不能熟练应用几何画板,所以笔者想借助另一种更易上手的软件——微软Math3.0来设计本节课。
微软Math3.0是微软公司近些年发布的一款功能强大的数学软件,比起几何画板,它更易上手,一般试用一两次就会使用,不仅能给老师们带来便捷,还能成为辅导学生课后研究的好帮手。
对于《函数y=Asin(ωx+φ)的图像》一课,利用微软Math3.0可以辅助提高教学效率。下面就教学方法和主要教学过程作以详细阐述。
一、教学方法
采用探究发现法,以物理中的实例为切入点,激发学生的求知欲,将信息技术融入整个教学过程中,将函数图像的变化过程直观动态地展现给学生,通过引导学生进行观察、思考、猜想、验证、归纳等数学活动,培养学生的探究能力、分析问题的能力以及抽象概括的能力。函数y=Asin(ωx+φ)涉及3个参数,先逐一探究各参数的作用,然后再将三个参数综合起来,使学生体会先局部后整体以及由特殊到一般的思想方法。
二、教学过程
1.设置情境,引入课题
教师:在物理和工程技术的许多问题中,经常会遇到形如y=Asin(ωx+φ)的函数,例如,在简谐振动中位移与时间表示的函数关系就是形如y=Asin(ωx+φ)的函数。那么,这个函数和正弦函数y=sinx有什么关系?换句话说,参数A、ω、φ对y=Asin(ωx+φ)的图像有什么影响?
学生讨论交流并回答:先分别考查A、ω、φ对y=Asin(ωx+φ)的图像的影响,然后再综合分析y=Asin(ωx+φ)和y=sinx的关系。
设计意图:培养学生先局部后整体的思想。
2.启发思考,探究新知
探究1:A对y=Asinx的图像的影响
设计意图:通过让学生自己作图,复习“五点作图法”并寻找图像间的关系,让学生体会研究三角函数问题的方法,培养学生数形结合的思想和分析问题的能力。
教师引导学生分析特殊点的坐标变化和以上三个函数的联系,不难得出:y=Asinx,x∈R(A>0,A≠1)的图像可以看作把正弦曲线上所有点的纵坐标伸长(A>1)或缩短(0 学生探究y=Asinx(A>0,A≠1)的性质:与y=sinx作比较,定义域、奇偶性、单调区间、周期性均没有发生变化;值域和最值发生了变化,y=Asinx的值域为[-A,A],最大值为A,最小值为-A。 教师将φ的值调回到0(此时y=sin(x+φ)即为y=sinx),点击拖动滑块向右滑动,让学生观察当φ>0时,y=sinx的图像怎样移动;再将φ的值调回到0,拖动滑块向左滑动,让学生观察φ<0时,y=sinx的图像怎样移动。 学生讨论交流φ对y=sin(x+φ)图像的影响,并归纳:函数y=sin(x+φ)的图像可以看作把正数曲线上所有的点向左(φ>0)或向右(φ<0)平移φ个单位长度得到的。 学生探究y=sin(x+φ)的性质:与y=sinx作比较,定义域、值域、最值、周期均没有发生变化;奇偶性和单调区间发生了变化。 教师:在函数y=sin(x+φ)中,φ决定了x=0时的函数值,通常称φ为初相,x+φ为相位。 探究3:ω对y=sinωx的图像的影响 探究方法类似探究2,此处不作详细说明。注意在探究过程中指导学生思考“为什么ω变大,图像反而横向收缩;ω变小,图像反而横向拉长了?” 探究4:如何由y=sinx的图像得到y=Asin(ωx+φ)的图像 (1)利用Math3.0的Graphing功能在两个函数输入框中输入y=sinx(作为对比图)和y=Asin(ωx+φ),作出它们在同一坐标系中的图像(此时A=1,ω=1,φ=0,并将A的取值范围设置为[0,3]); 教师用Math3.0演示如下: (1)同前一种变换第1步; 最后,教师引导学生梳理知识,总结由y=sinx的图像得到y=Asin(ωx+φ)的图像的两种变换方法。 以上是对《函数y=Asin(ωx+φ)的图像》一课的主要内容的设计。Math3.0软件是一种便捷的数学教学工具,合理地使用它可以给我们的数学课堂带来活力,提高教学效率。

