基于6σ稳健性的车门多学科优化设计

朱茂桃 郭佳欢 钱洋 刘涛

（江苏大学）

基于6σ稳健性的车门多学科优化设计

朱茂桃 郭佳欢 钱洋 刘涛

（江苏大学）

为了提高优化后车门性能的稳健性，结合有限元分析与试验验证，提出一种综合考虑质量、刚度与1阶振动模态的多学科优化设计方法——基于6σ稳健性的车门多学科优化设计方法。由于该方法综合了试验设计、径向基函数模型、蒙特卡罗模拟技术和自适应模拟退火算法等优势，与传统确定性优化结果相比，在获得近似最优解的同时能够提高设计变量的可靠性和目标函数的稳健性，大幅度提高产品质量。

1 前言

在传统车门结构优化设计中，由于忽略了车门在制造中存在的许多不确定性因素，如零部件厚度及材料性能参数的随机波动等，可能导致车门的品质特性响应（如刚度、强度和模态等）表现为概率分布，使设计超出约束条件而失效，从而使优化方案缺乏可靠性[2]。为此，有学者采用6σ稳健优化设计方法，将6σ质量管理、可靠性优化设计和基于容差模型的稳健优化设计相结合，使响应均值远离约束，并减小响应偏差，能够同时提高设计的可靠性和稳健性[3]。

本文根据某车门刚度和模态分析结果，将6σ稳健优化设计和多学科优化设计相结合应用在车门的结构优化中，充分考虑车门各部件板厚和材料特性的不确定性，利用拉丁方试验设计构造出高精度的径向基函数模型，结合基于蒙特卡罗模拟技术的6σ分析和自适应模拟退火算法，构造了基于6σ稳健性的车门多学科优化设计方法。

2 车门有限元模型的建立与验证

本文研究对象是由厚度不足2 mm的薄板经冲压焊接而成的车门（图1），其长度方向尺寸远大于厚度方向尺寸，符合壳单元的理论假设，因此本文主要采用壳单元进行离散化[4]，网格大小为10 mm，并对单元参数进行控制。焊点采用rigid刚性单元模拟。整个车门统一采用08 AL材料，弹性模量为207 GPa，泊松比为0.3，密度为7 800 kg/m3。

利用Hypermesh软件建立的车门有限元模型如图2所示，包含26 300个节点、25 546个单元，其中有24 447个四边形单元，633个三角形单元，466个刚性单元。

通过Optistruct求解器，分别对车门的下沉刚度、扭转刚度、外板静压刚度和模态性能进行了有限元分析，分析计算结果如图3所示。由图3可知，车门右上角扭转刚度明显不足，变形达到12.05 mm，大于该企业的评价标准（10 mm）。车门1阶模态振型如图4所示，

表现为外板上部窗框处弯曲，窗框下边沿弯曲变形最大。车门1阶模态频率值为34.83 Hz，与一般情况下轿车车身1阶固有频率相近，存在共振的可能，故需要进行扭转刚度和模态性能的优化，即在满足车门扭转刚度和模态性能要求的前提下，以车门质量最小化为目标函数进行多学科优化设计。

为验证车门有限元模型的正确性，对车门进行模态试验，并将车门的试验模态与理论模态进行对比分析。试验模态采用固定单点锤击，逐点拾取响应信号，测点布置采用100 mm×100 mm间距，共有109个测点。测试系统组成如图5所示。

激励信号与响应信号经过ICP放大器输入到SD380动态信号分析仪，经过FFT分析得到激励点与响应点之间的频率响应传递函数。在STAR分析软件中利用多项式拟合法对所有频响函数进行曲线拟合，通过模态参数识别，得到车门模态参数。

将试验模态分析结果与理论模态结果进行比较，对比结果如表1所示。

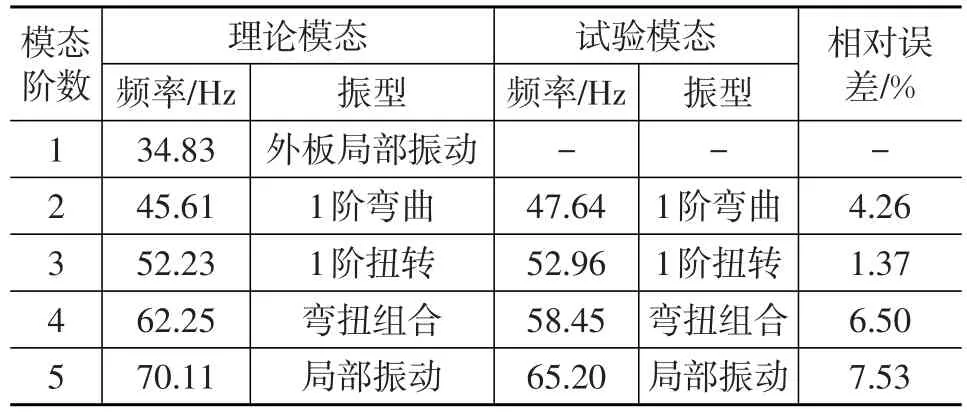
表1 车门理论模态与试验模态结果对比

由表1可知，前5阶模态中，试验模态比理论模态要少1阶频率，总体来看是由于理论模态分析中所搭建的模型节点数远远超过试验模态中的测点数，从而导致一些理论模态在试验中没有出现。总体而言，相对应的理论模态和试验模态频率值、振型较为一致,其中第5阶模态频率相对误差值最大，达到7.53%，但仍满足小于10%的误差要求。这主要是由于有限元模型的简化、焊点位置模拟不准确以及试验中不可避免的误差造成。

综上所述，车门理论模态分析与试验模态分析的频率相近、振型相似，因此该有限元模型有效反映了车门实体属性，能够用于多学科稳健优化的研究。

3 基于试验设计的径向基函数模型构建

3.1 试验设计

代理模型是包含试验设计和近似方法的综合建模技术。建立高精度的代理模型很大程度上取决于对设计空间的采样技术。用合理的试验设计方法均匀分布样本点，可以有效保证近似模型的精度。本文采用拉丁方试验设计，它是一种基于随机抽样的试验设计方法，具有均衡分散性和整齐可比性等特点，适用于多因素、采样空间大的研究。

在Hyperstudy软件中，设定车门内板厚度T1、外板厚度T2、内板加强板厚度T3、外板加强板厚度T4、门锁加强板厚度T5、门锁支承加强板厚度T6、铰链支承加强板厚度T7、防撞梁厚度T8以及车门材料的弹性模量E、泊松比μ和密度ρ为设计变量，并设置质量m、扭转工况最大变形d和1阶固有频率f为3个不同类型的响应。按表2中设计变量的范围，应用拉丁方试验设计进行11因素150水平的试验设计，对因素的每个水平进行一次试

验，从而获得150组因素与响应对应关系的样本数据。

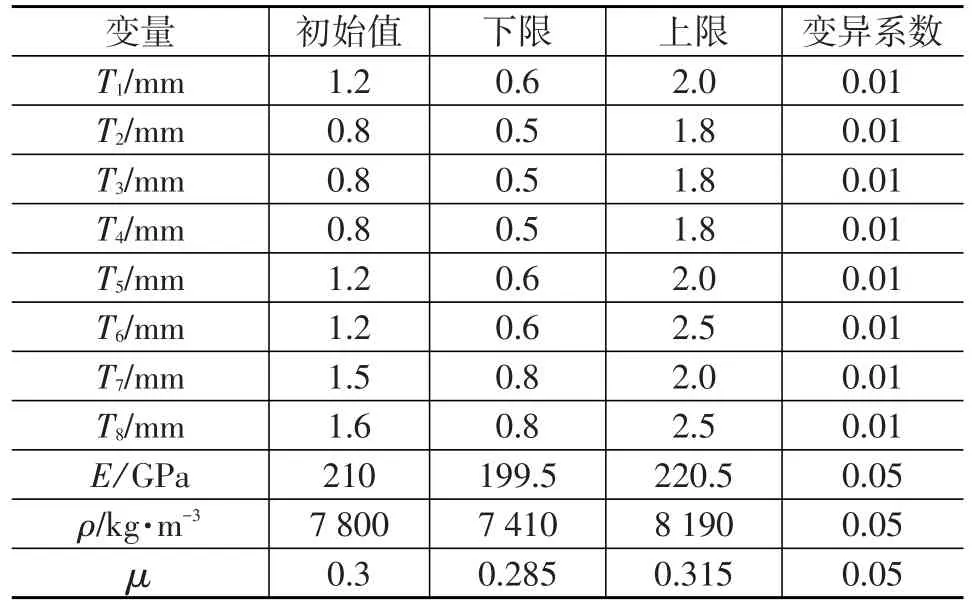
表2 设计变量

3.2 径向基函数模型

总结相关研究成果可以发现[5]，径向基函数（Radi⁃cal based functions,RBF）模型适用性较强，但Kriging模型则对数据采样要求较高，对数值噪声的敏感性制约了其应用；多项式响应面（Response surface method, RSM）模型在解决低变量数、低阶非线性问题方面具有上佳表现。本文研究的车门多学科稳健性优化设计属于多变量、非线性问题，因此选用RBF模型。

为了保证优化设计结果的精确度，代理模型的精度显得尤其重要，本文从两个方面检查其精度：一是用决定系数R2评价代理模型对样本点的拟合情况，其值越接近1则代理模型精度越高；二是检查代理模型在非试验样本点的精度，可在设计空间中随机生成一组测试样本点，检查代理模型结果和有限元模型结果的相对误差，误差越小则代理模型精度越高。

在iSIGHT软件Approximation组件中，利用上述拉丁方试验设计的150个样本数据，建立了三个不同学科响应的RBF模型，其决定系数R2的值如表3所示。分析表3可知，质量响应的模型精度最高，扭转变形响应模型的精度次之，而1阶频率响应模型的精度最低，这是1阶频率响应的非线性程度最高的原因，但总体而言，3个不同学科类别的响应模型决定系数均大于0.9，故该代理模型对样本点的拟合精度符合要求。

表3 RBF模型决定系数

采用拉丁方试验设计对设计空间抽样12个样本点，应用RBF模型获得对应的质量、扭转变形和1阶频率响应的预测值，并与有限元模型的实际计算值相比较，相对误差表达式如式（1）所示：

式中，y为车门有限元模型计算值；y~为车门RBF模型预测值。

3种响应的RBF模型在12个样本点处的相对误差值如图6所示。

从图6可看出，车门质量模型精度最高，扭转工况下最大变形的模型精度次之，而1阶固有频率的模型精度最低，个别样本点相对误差接近8%，这同样是由于1阶固有频率响应的非线性程度最高、扭转变形次之，而车门质量响应的线性程度最高所致。总体而言，3个不同学科的响应面模型精度均较高，响应面模型均可代替真实模型进行优化计算和稳健优化设计。

4 基于ISIGHT软件的6σ稳健优化设计

4.1 6σ稳健优化

6σ稳健优化设计要求产品质量在均值6σ范围波动时均满足设计要求。

6σ稳健性优化数学模型为：

式中，F为稳健性优化的目标公式；μy、μg和μx分别是响应y、g和变量x的均值；σy、σg和σx分别为响应y、g和变量x的标准差；n为σ水平，当n=6时，称为6σ稳健性优化设计。

目标函数可描述为：

式中，ω1、ω2为权因子。

在iSIGHT平台中进行6σ稳健设计可以做到考虑设计变量、约束和设计目标的所有不确定性因素，确定差错率或可靠率，优化到既定的可靠性水平，使得由不确定参数引起的响应波动最小，将6σ质量水平描述到设计中去[6]。而6σ稳健性优化设计需要计算响应的均值和方差，常用方法有矩法、解析法和蒙特卡罗模拟法。本文采用的是蒙特卡罗模拟法，对应于iSIGHT中

基于均值可靠性分析方法的6σ稳健优化。

4.2 优化过程

综合考虑车门的成本和工艺要求，确定合理的设计变量范围。根据工程经验和相关研究成果可知，各设计变量均符合正态分布，取值范围和变异系数见表2。

根据前文中车门有限元分析结果，确定在满足车门扭转刚度和模态性能约束条件下，以车门质量最轻为目标函数进行多学科优化设计。在iSIGHT软件中对该问题进行确定性优化和6σ稳健优化，整个优化流程图如图7所示。

该问题的确定性优化数学模型为：

相应的6σ稳健性优化数学模型为：

初始设计条件见表4，车门质量为17.8 kg，扭转工况最大变形为12.05 mm，1阶固有频率为34.83 Hz，得知车门扭转刚度和1阶固有模态不满足约束条件，因此需要对该车门进行优化。选取表2中车门8个部件厚度为设计变量，利用自适应遗传退火算法对RBF代理模型进行优化[7]，得到确定性最优解（表4），并对确定性最优解进行6σ质量分析。再根据表2中各变量的初始条件、范围、分布类型和变异系数，选取车门8个部件厚度为随机设计变量，考虑弹性模量E、泊松比μ和材料密度ρ共3个随机噪声的影响，采用基于蒙特卡罗模拟技术的6σ分析法和自适应遗传退火算法进行稳健优化。6σ稳健性优化设计相当于在每次确定性优化后进行稳健性评估，另外，6σ稳健性优化的收敛迭代次数相对确定性优化有所增加。

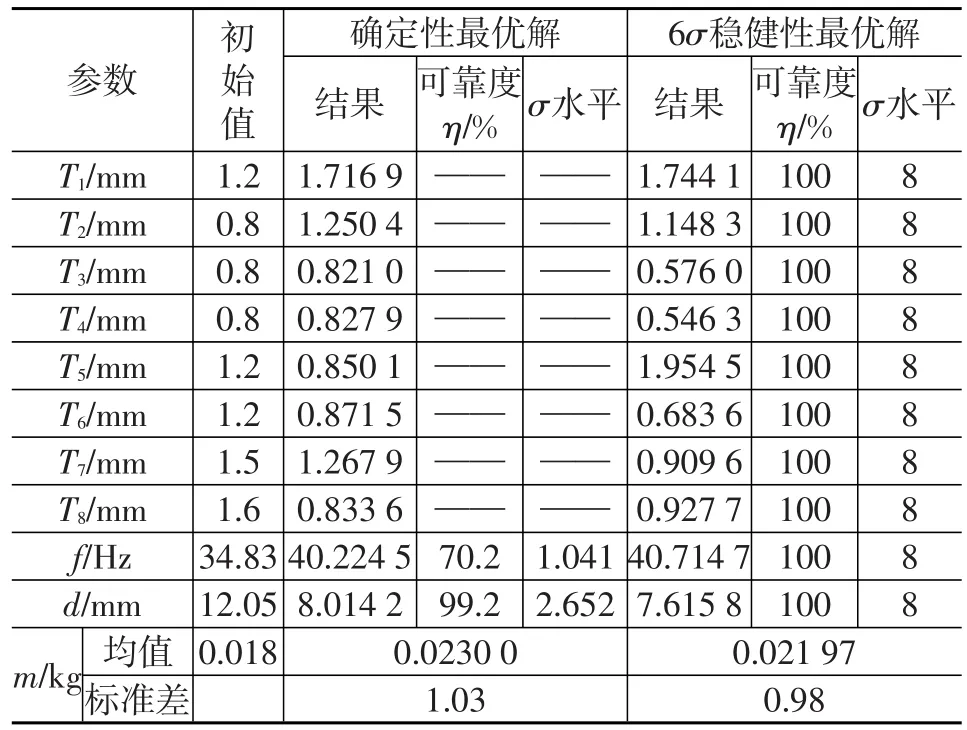
表4 优化结果对比

4.3 优化结果分析

从表4中确定性优化结果看，约束f只有1.041σ水平，可靠度仅为70.2%；同样，约束d的σ水平数为2.652，可靠度为99.2%。而从6σ稳健优化结果看，设计变量和约束函数都达到了8σ水平，可靠度为100%，每百万缺陷数为0。将确定性优化结果与6σ稳健优化结果对比可知，6σ稳健优化设计不仅将目标函数的均值和标准差同时降低，使产品质量的一致性得到提高，而且使得设计变量远离边界约束，达到8σ水平，可靠度达到100%。

1 张平，雷雨成，高翔，等.轿车车身模态分析及结构优化设计.汽车技术.2006（04）：5～9.

2 Maglaras G,Ponslet E,Halftka R T,et al.Analytical and Ex⁃perimental Comparison of Probabilistic and Deterministic Optimization.AIAA Journal,1996,34（7）:1512～1518.

3 Youn B D,Choi K K,Yang R J,et al.Reliability based de⁃sign optimization for crashworthiness of vehicle side impact.Structural and Multidisciplinary Optimization,2004,26（3-4）:272～283.

4 李玉强，崔振山，陈军，等.基于响应面模型的6σ稳健设计方法.上海交通大学学报，2006,40（2）:201～205.

5 谷海涛，林扬，胡志强，等.基于代理模型的水下滑翔机机翼设计优化方法.机械工程学报，2009,45（12）:7～14.

6 赵秀婷，张文明，申炎华，等.基于iSIGHT的湿式多盘制动器稳健设计.工程机械,2006,37:36～39.

7 黄石华，成艾国，胡朝辉，等.基于稳健性的拼焊板车门轻量化研究.汽车工程，2011,33（3）:262～266.

（责任编辑 帘 青）

修改稿收到日期为2015年11月1日。

Multidisciplinary Design Optimization of Car Door Based on Six Sigma Robustness

Zhu Maotao,Guo Jiahuan,Qian Yang,Liu Tao
（Jiangsu University）

To improve the robustness of the optimized car door’s performance,a car door multidisciplinary design optimization based on Six Sigma,which considers mass,stiffness and the first order vibration mode is proposed.Since this method integrates design of experiment,RBF model,Monte Carlo simulation technique and adaptive simulated annealing method,so compared with the traditional deterministic optimization results,this method not only obtains an approximate optimal solution,but also improves the reliability of design variables and the robustness of the objective function,and the product quality can also be improved greatly.

Car door,Multidisciplinary design optimization,Six sigma robustness,RBF model

汽车车门 多学科优化设计 6σ稳健性 径向基函数模型

U463.83+4

A

1000-3703（2015）12-0004-04