基于ARMA模型的桥梁结构模态参数辨识研究

赵 瑜，薛 白，张建伟

(华北水利水电大学，河南 郑州 450045)

我国桥梁大多建于20 世纪60 ～80 年代，当时的设计标准较低，且施工质量不是很高．随着交通运输量的不断增加，车辆载重不断提高，超载车辆对桥梁的损坏也愈发严重． 我国在桥梁损伤检测方面面临严峻的形势，要准确地判断桥梁实际工作的状况，为桥梁加固或大修提供依据，就必须找到可靠、精确的损伤检测方法．加之新兴结构不断出现，结构的复杂程度也不断增加，要使日趋复杂的结构的安全性能得到保证，结构的振动设计就变得尤为重要．无论损伤检测还是结构振动设计，都离不开模态参数辨识，它在结构的动态特性分析中起着至关重要的作用．

模态参数辨识的方法可以分为频域辨识方法和时域辨识方法两大类． 频域参数辨识首先要把从响应点测得的时域信号经过A/D 转换与FFT 变换，变成频域信号，然后将频域数字信号进行预算，求得频率响应函数，再按参数辨识的方法辨识出模态参数［1］．而时域模态参数辨识则无需将所测得的时域信号变换到频域中去，而是直接在时域中进行参数辨识，这就避免了由数据变换(FFT 变换)而引起的误差，从而提高了参数估计的精度．

时域辨识方法最早可追溯到1927 年，英国统计学家G．U． Yule 提出了自回归(Autoregressive，AR)模型．后来，英国数学家、天文学家G T Walker(1931年)在分析印度大气规律时引入了滑动平均模型(Moving Average，MA)和自回归滑动平均模型(Autoregressive Moving Average，ARMA)，这些时间序列模型奠定了时域辨识方法的基础［2］． 时域法可以仅从响应数据中辨识模态参数，而无需激励数据，这对于那些激励信号无法测得的工程结构来说非常重要．比如，一些海上作业平台或水工建筑物在风浪及大地脉动作用下的振动，它们所受到的荷载往往很难测量．时域法给对工作状态下的机械或工程结构进行模态分析提供了可能，在工作状态下辨识的模态参数更能反映结构的实际动态性能． 随着研究的深入，模态参数时域辨识领域不断有新的方法出现．在诸多方法中，时域法由于在辨识过程中具有无能量泄露、分辨率高等优点，在模态辨识领域中得到了广泛应用．

ARMA(Autoregressive Moving Average)模型相比于AR(Autoregressive)模型更复杂，计算更繁琐，但是每一部分模型参数的物理意义也更明确． 由于多了表征与外界联系的MA(Moving Average)部分，因而更能充分考虑到外界因素的影响，故精度更高．ARMA 模型相比于AR 模型，识别结构因损伤而引起的动力学特征的微小变化有更强的能力． 笔者将结合试验对基于ARMA 模型的模态参数辨识方法进行讨论，在噪声模态的剔除问题上引入了稳定图方法，可以直观地从稳定图中识别出系统的固有频率，有效地剔除噪声模态．

1 基本理论

1．1 ARMA 时间序列模型

ARMA 模型(自回归滑动平均模型)是时序方法中最基本、应用最广的时序模型．对于平稳、正态、零均值的时序{xt}，若xt的取值不仅与其前p 步的各个取值xt－1，xt－2，…，xt－p有关，而且还与前q 步的各个干扰项εt－1，εt－2，…，εt－q有关(p，q=1，2，…)，则按多元线性回归思想，可以得到ARMA(p，q)的一般形式:

式(1)表示一个p 阶自回归、q 阶滑动平均模型，记为ARMA(p，q);其中p，q 分别表示AR 部分和MA 部分的阶次;i(i =0，1，…，p)为自回归系数;εt为零均值、方差为σ2的白噪声序列;θj(j =0，1，…，q)为滑动平均系数．

若Bixt=xt－i，则式(1)可变换为:

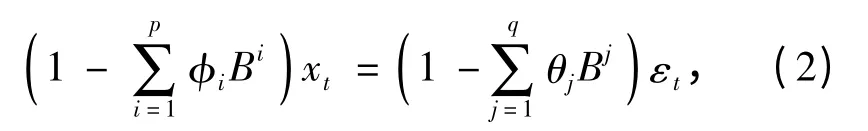
令

则式(2)可化简为

因此有

式(4)从系统动力学的角度来理解，若将εt视为输入，将xt视为输出，则ARMA(p，q)模型就描述了一个传递函数为θ(B)/(B)的系统［3］，由下文可知分母(B)包含系统的特征频率及阻尼比．

1．2 模型定阶

建立模型时，根据AIC［4］准则函数取值来判断模型的优劣，使准则函数达到极小值的是最佳模型，该准则是在模型极大似然估计的基础上建立起来的．

最小信息准则AIC 函数的一般形式为

式中:ML 为模型极大似然度，一般用似然函数表示;K 为模型中独立参数个数．

当样本长度N 充分大时，ARMA 模型得到近似极大似然估计的对数似然函数:

由于式(6)中第二项与模型及参数个数无关，可以舍弃．于是得到采用ARMA(n，m)模型拟合的AIC 准则函数:

使得AIC 信息量取值最小的n 和m 即是模型理想的阶．由式(7)可以看出AIC 信息量由两部分构成:前一部分体现模型的拟合好坏，后一部分表明模型参数的多少． 显然，模型拟合得越精确越好，但过高的精度要求又会导致参数的增多及模型的复杂，可能反而影响模型的拟合效果． 因此，实质上就是对拟合精度和参数个数二者加以适当权重． 可以想象，当模型中参数个数K 由少至多增加时，拟合误差改进显著，式(7)中第一项起主要作用，AIC 明显下降;随着模型阶数的增加，模型拟合残差改进甚微，AIC 上升． AIC 的最小值处对应着最佳模型的阶数．

1．3 ARMA 模型参数与系统模态参数的关系

ARMA 时序模型是一个参数模型，如果不能清楚解释其每个参数的物理意义，也就无法判断该模型是否能够真实准确地模拟一个结构．然而，如果在ARMA 模型参数与系统模态参数之间建立联系，实现模型参数到系统模态参数的转换，就能达到通过激励数据和结构响应数据辨识结构模态参数的目的［5］．

首先用测得的结构响应数据建立一个ARMA(2n，2n－1)模型，然后将离散的ARMA(2n，2n －1)模型转化为连续模型． 离散模型自回归部分的特征根与连续模型自回归部分的特征根之间有如下关系:

其中Δ 为采样时间间隔．

结构第j 阶模态固有频率ωnj、模态阻尼率ξj与特征根之间关系如下:

由式(8)得

将式(9)代入式(10)化简得

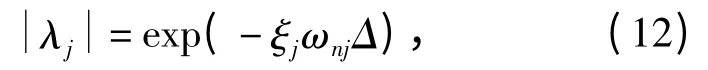
两边取对数，有

将式(11)代入式(13)得

由式(11)和式(14)不难看出，根据ARMA(2n，2n－1)模型自回归部分的特征根即可求出结构模态参数:固有频率ωnj和模态阻尼率ξj．

1．4 噪声模态剔除

由于试验过程中存在噪声的干扰，使得识别出的模态既有结构固有的模态又掺杂着噪声模态，这就需要采取措施从识别出的模态中剔除噪声模态．然而，单从一组数据进行一次模态识别得出的频率无法判断哪些频率是结构固有的频率．但是，若把每组数据识别出的模态频率按序号描在一张图上，再根据结构固有频率与噪声频率对应的点各自在图中排成形状的差异，即可辨别出结构固有频率．以数据组序号为纵坐标，以频率大小为横坐标描出的散点图称为稳定图．

稳定图同时也是每组数据模态识别结果的记录图，不仅能够清楚地反映每组数据识别出的模态频率大小，还能反映出不同组模态识别结果之间的关系．若相邻几组识别结果差异很大，且无规律，在稳定图中表现为出现一些不规则排列的离散点． 若相邻几组识别结果相同或差别不大，在稳定图中表现为出现一些排成竖直直线的点．

噪声具有不稳定性，有的噪声信号会间断，有的频率会随着时间变化，致使每组数据识别出的噪声模态会有较大差异，在稳定图上的表现是出现无规律的离散点及排成曲线的稳定图极点［6－7］． 而系统固有的频率十分稳定，因而每次识别出的频率在稳定图中会排成一条无间断的直线． 根据这点区别就很容易从稳定图中辨识出系统的固有频率．

2 数值试验验证

试验构件为一块长5．0 m，宽1．0 m，厚0．2 m的板，沿板长方向对称布置了11 个位移传感器，试验模型如图1 所示．

图1 单跨桥梁试验模型

在用ARMA 模型法计算板的模态频率时，只需要用到跨中位置测点的数据．在环境激励下，记录梁的响应数据，采样频率为256 Hz，采样时间为40 s，共测得跨中位置处位移响应数据10 240 个，如图2 所示．

图2 位移响应数据

经过小波消噪后取其中8 384 个作为试验样本，建模前还需要对这些数据进行零均值、稳定化处理，图3 为经消噪、零均值、稳定化处理后的响应数据．以2 048 个数据为1 组，分段滞后64 个点，将试验样本分为100 组． 首先对这100 组数据分别用AIC 准则进行定阶，发现AR 部分的阶数能够稳定在16 阶，据此采用理论阶次ARMA(2n，2n －1)，将模型阶数定为ARMA(16，15)．

模型阶数确定之后，用最小二乘法估计模型参数，再结合上述模型参数与系统模态参数的关系即可识别出系统的频率． 以每组数据的序号作为纵坐标，以频率大小作为横坐标做出系统频率稳定图，如图4 所示．

图3 经消噪、零均值、稳定化处理后的响应数据

图4 频率稳定图

从图4 中可以清楚地看到，各个点连成了多段曲线，其中由于系统固有频率较为稳定，每组数据识别出的结果变化不大，从而在图中排成了3 条纵向的连续直线．它们分别对应着系统的3 阶固有频率，而其他弯曲程度较大或者有间断的曲线则是由噪声产生的虚假模态．由于建模所用的时间序列是经过消噪处理的，因此这些残余噪声产生的虚假模态具有明显的离散性，这就使得真实模态与虚假模态在图中很好区分．

为了验证基于ARMA 模型的模态参数辨识法识别出的模态参数的正确性，将识别结果与ANSYS建模分析法和随机子空间法的计算结果进行对比，分析3 种方法识别出的模态频率是否吻合．用Solid65单元模拟混凝土结构［7］，在ANSYS 中建立混凝土简支梁的有限元模型，经过模态计算得出简支梁前3阶模态，模态频率见表1．各阶模态所对应的模态振型如图5 所示，其中第1 阶振型呈正对称图形，第2阶振型为反对称“S”型图形，第3 阶振型是结构发生扭振．将稳定图中识别出的频率与用随机子空间法识别出的模态频率及ANSYS 建模分析计算出的模态频率比较发现，3 种方法识别出的3 阶频率基本吻合，这就表明用ARMA 法能够准确地识别出结构的模态频率．

表1 不同方法识别频率比较

图5 ANSYS 建模计算出的前3 阶模态振型

3 结 语

用ARMA 模型识别系统频率并结合稳定图法辨识结构的模态频率的方法能够方便而准确地识别出结构的模态频率． 该方法不仅适用于实验室中的小型构件，同样适用于实际工程结构的模态参数识别．但是，基于环境激励下的模态参数识别由于激励不可控，往往存在激励不充分、不平稳的问题，这就导致较高阶次的模态很难识别或者识别不准确，因此在识别高阶模态时还需要进行算法上的改进．

［1］张建伟，张翌娜，赵瑜． 泄流激励下水工结构应变模态参数时域辨识研究［J］． 水力发电学报，2012，31(3):199 －203．

［2］张建伟，康迎宾，张翌娜，等．基于泄流响应的高拱坝模态参数辨识与动态监测［J］．振动与冲击，2010，29(9):146 －150．

［3］张建伟，李火坤，练继建，等．基于环境激励的厂房结构损伤诊断与安全评价［J］． 振动、测试与诊断，2012，32(4):670 －674．

［4］刘卫东，刘尚合，胡小锋，等．小波阈值去噪函数的改进方法分析［J］．高压电技术，2007，33(10):59 －63．

［5］赵志宏，杨绍普，中永军． 一种改进的EMD 降噪方法［J］．振动与冲击，2009，28(12):35 －37．

［6］李惠彬．大型工程结构模态参数识别技术［M］． 北京:北京理工大学出版社，2007．

［7］练继建，李火坤，张建伟． 基于奇异熵定阶降噪的水工结构振动模态ERA 识别方法［J］． 中国科学，2008，38(9):1398 －1413．