两边连接屈曲约束钢板墙边缘构件的受力规律

刘文洋+李国强

摘要：利用理论分析和有限元方法对两边连接屈曲约束钢板墙边缘构件（梁）的受力规律进行研究，提出了两边连接屈曲约束钢板墙与边缘构件的传力模型和边缘构件内力计算方法。利用等效支撑模型对所提出的边缘构件内力计算方法进行了验证，对不同层数和跨数的框架-屈曲约束钢板墙结构和框架-等效支撑结构进行分析，对梁、柱构件的内力进行了对比，分析了屈曲约束钢板墙布置方式对边缘构件内力、变形的影响。结果表明：所提出的方法能够准确计算屈曲约束钢板墙边缘构件的内力；建议屈曲约束钢板墙的宽度宜设计成大于跨度的1/3，并将屈曲约束钢板墙布置在跨度中间；如果屈曲约束钢板墙的宽度只能小于跨度的1/3，则宜布置在靠近梁端部。

关键词：屈曲约束钢板墙；边缘构件；受力规律；有限元分析；传力模型

中图分类号：TU392.4 文献标志码：A

0 引 言

屈曲约束钢板剪力墙（简称屈曲约束钢板墙，BRSPSW）是在普通钢板墙两侧设置盖板，盖板的作用仅是抑制内嵌钢板的屈曲而并不参与结构的抗侧力和刚度。由于屈曲约束钢板墙从构造上抑制了内嵌钢板的屈曲，因此抗侧力滞回曲线较为饱满，耗能能力和承载力较普通钢板墙显著增强。屈曲约束钢板墙的连接方式通常包括四边连接和两边连接，四边连接是指内嵌钢板四边均与梁、柱构件连接，而两边连接是指内嵌钢板只与水平边缘构件（梁）连接。

各国学者对普通薄钢板墙与边缘构件的传力规律和边缘构件的受力影响已经开展了大量研究，基本解决了这些问题，四边连接屈曲约束钢板墙与边缘构件的传力规律也已明确。1983年Thorburn等[1]对四边连接普通薄钢板墙的受力性能进行了系统研究，指出薄钢板墙在屈曲后可通过形成斜向拉力带来继续抵抗水平剪力直至材料受拉屈服，并提出用一系列两端铰接的等效拉杆来代替普通钢板墙进行受力分析，给出了等效拉杆倾角计算公式。随后Timler等[2]基于最小能量原理修正了Thorburn等提出的等效拉杆倾角计算公式，该模型已被写入美国和加拿大规范[3-4]。Thorburn等[1]和Park等[5-6]利用该等效拉杆模型分析了普通钢板墙对边缘构件受力的影响。对于中间层梁，上下均有钢板墙，因此2块钢板墙传来的力互相抵消，钢板墙对梁的影响可以忽略不计。然而对于柱，只有单侧布置钢板墙，因此钢板墙传给柱的斜向力既会增加柱的轴力，同时也会对柱产生附加弯矩。周明[7]采用Thorburn等提出的等效拉杆模型分别对单层单跨和四层三跨框架-普通钢板墙结构进行受力分析，研究了普通钢板墙对框架梁、柱内力的影响。同时，研究发现对于厚钢板墙等效拉杆模型的误差较大，因此提出了适用于不同厚度钢板墙且相对较为精确的统一等代模型。

孙飞飞等[8-9]对两边和四边连接组合屈曲约束钢板墙的受力性能进行了研究，考虑由于实际的混凝土盖板不能为屈曲约束钢板墙提供完全的面外约束，提出用双向多斜杆模型代替组合屈曲约束钢板墙以模拟其对边缘构件的作用。陆烨[10]利用有限元参数分析的方法对Ⅰ型屈曲约束钢板墙和所提出的等效支撑模型引起的框架梁弯矩进行了对比分析，以保证支撑点位置的合理性，但该模型仅适用于大高宽比Ⅰ型屈曲约束钢板墙。郭彦林等[11]、周明[7]对四边连接屈曲约束钢板墙与框架的相互作用进行了分析，认为四边连接屈曲约束钢板墙接近平面应力状态，屈曲约束钢板墙对边缘框架柱基本上只产生附加轴力，并提出用拉、压强度相等及倾角为45°的双向多斜杆等代模型来代替屈曲约束钢板墙。

综上所述，目前对两边连接屈曲约束钢板墙的研究主要集中在墙体自身的受力性能或框架-屈曲约束钢板墙整体结构受力性能，对两边连接屈曲约束钢板墙与边缘构件之间的传力规律及屈曲约束钢板墙对边缘构件的受力影响还研究得较少。本文利用理论分析和有限元方法对两边连接屈曲约束钢板墙边缘构件的受力规律进行研究，给出边缘构件的内力计算方法，并针对屈曲约束钢板墙的布置方式提出设计建议。如无特殊说明，本文所提出的屈曲约束钢板墙均指两边连接屈曲约束钢板墙。

1 两边连接屈曲约束钢板墙与边缘构件的传力规律 两边连接屈曲约束钢板墙是把内嵌钢板仅在上、下端与梁相连，这样处理一方面可以避免屈曲约束钢板墙对柱的直接影响，另一方面也有利于屈曲约束钢板墙的灵活布置，便于门窗洞口的开设。

文献[12]中的研究表明，当屈曲约束钢板墙的高宽比小于1.5时，屈曲约束钢板墙两侧各存在一个边缘约束区，其宽度约为屈曲约束钢板墙净高的1/3，且与高宽比、厚度等参数基本无关。边缘约束区对中间屈曲约束钢板墙形成约束，起到竖向边缘构件的作用，因此屈曲约束钢板墙中间部分的受力特点与四边连接屈曲约束钢板墙相同，主要受剪应力作用，可称之为中间剪切区。两边连接屈曲约束钢板墙与边缘构件（梁）的传力可按中间剪切区和边缘约束区分别进行分析。中间剪切区处于纯剪切状态，在该范围内屈曲约束钢板墙与梁只传递沿水平方向均匀分布的剪力。两侧边缘约束区传给梁的力是斜向力，但该斜向力与竖直方向的夹角很小，可忽略其水平分量，只考虑力的竖向分量，即认为边缘约束区传给梁的力主要是垂直于梁轴线方向均匀分布的拉力或压力。因此两边连接屈曲约束钢板墙与边缘构件（梁）的传力模型可采用如图1所示的形式。图1中，σ为应力，τ为剪应力。当屈曲约束钢板墙

端部截面屈服时，边缘约束区的应力达到屈服应力，而中间剪切区的应力达到剪切屈服应力。

当屈曲约束钢板墙高宽比大于等于1.5时，屈曲约束钢板墙以弯曲受力为主，不存在中间剪切区，此时屈曲约束钢板墙与边缘构件（梁）的传力可只考虑竖向的正应力，忽略水平方向的剪应力。正应力的分布可近似视为屈曲约束钢板墙在受弯时符合平截面假定，即正应力呈斜直线分布。2 边缘构件的内力计算方法

2.1 梁和柱的内力

两边连接屈曲约束钢板墙会对梁产生横向力，进而改变梁的剪力和弯矩大小及分布，同时也对梁产生轴力。梁中剪力和弯矩的计算可根据框架在屈曲约束钢板墙边缘约束区合力点处作用如图2所示的外力引起的剪力、弯矩与框架在其自身分担的水平力作用下引起的剪力、弯矩相叠加得到，应该注意的是梁的最大弯矩控制截面可能在梁端也可能在等效支撑点处，设计时应取两者中的较大值。当梁上、下均布置屈曲约束钢板墙时，应考虑两侧屈曲约束钢板墙传递的荷载。图2中，V为结构的层间剪力，Vp为屈曲约束钢板墙分担的水平力，Vf为框架分担的水平力，α为边缘约束区合力点所连斜对角线与水平方向的夹角。

两边连接屈曲约束钢板墙不对柱直接产生影响，但会通过梁把力传递给柱，进而改变柱的轴力、剪力和弯矩大小及分布。柱中内力的计算可根据框架在图2所示的外力作用下引起的轴力、剪力、弯矩与框架在其自身分担的水平力作用下引起的轴力、剪力、弯矩相叠加得到。多高层结构的受力状态可以在图2所示的单层结构受力基础上得到，即每个层间均在布置屈曲约束钢板墙的跨间施加图2所示的外力。

2.2 内力计算模型

为便于在结构设计软件中对框架-两边连接屈曲约束钢板墙结构进行受力分析，图2中的受力状态可利用文献[12]提出的等效支撑模型（图3）代替。图3中，e为等效支撑点距墙边缘的偏心距，l为框架跨度，当屈曲约束钢板墙高宽比小于1.5时，取e=0.1h，h为屈曲约束钢板墙高度，当屈曲约束钢板墙高宽比大于等于1.5

图3 屈曲约束钢板墙等效支撑模型

Fig.3 Equivalent Brace Model of BRSPSW时，取e=b/6，b为屈曲约束钢板墙宽度。当等效支撑达到屈服时，支撑传给梁的力即对应图2中屈曲约束钢板墙对框架的传力状态。可采用该内力计算模型对整体结构进行受力分析，计算框架梁、柱构件的内力（弯矩、剪力和轴力）。

2.3 准确性验证

为验证所提出的内力计算模型的准确性，采用ABAQUS有限元分析软件对表1中的3个框架-两

边连接屈曲约束钢板墙结构和相应的框架-等效支撑结构进行受力分析，计算框架梁、柱构件的内力（弯矩、剪力和轴力）。所选结构分别为单层单跨、多层单跨和多层多跨框架-两边连接屈曲约束钢板墙结构，见图4～6。屈曲约束钢板墙采用壳单元S4R，厚度均为6 mm，钢材为Q235。梁、柱采用梁单元B21，钢材为Q345。支撑采用杆单元T3D2，材料均为理想弹塑性模型。屈曲约束钢板墙在跨间居中布置，全部模型在结构顶点位移加载至结构总高度的1/50（此时等效支撑已经完全屈服）。对极限状态下框架-屈曲约束钢板墙结构和框架-等效支撑结构中梁、柱构件的内力进行对比，限于篇幅仅列出了部分构件的对比图，见图7～9。

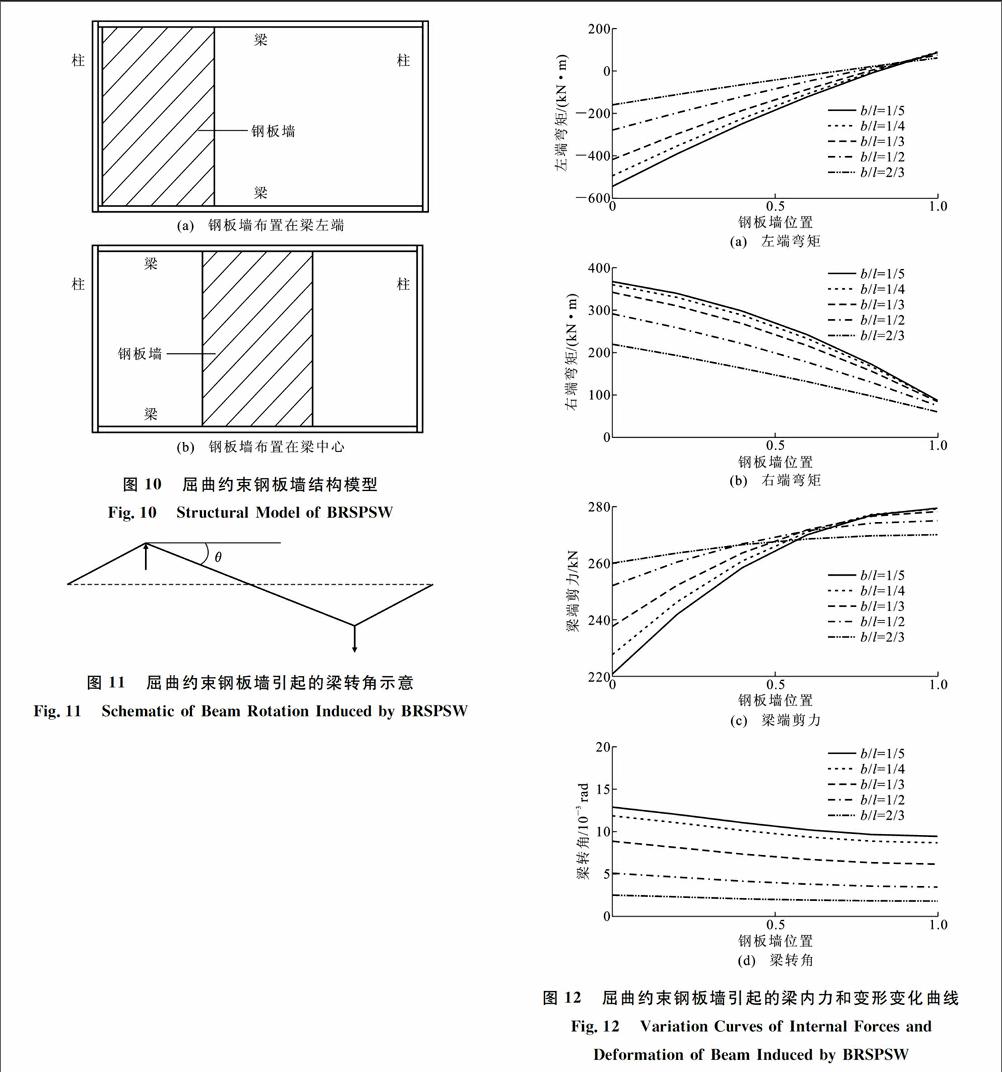
由图7～9可以看出，利用等效支撑模型得到的梁、柱构件内力与实际的屈曲约束钢板墙结构吻合得较好，特别是控制截面的内力基本一致。这不仅对于单层单跨结构具有较高的精度，而且对于多层多跨结构也能很好地模拟屈曲约束钢板墙对框架的传力。因此，可以采用简化的等效支撑模型进行屈曲约束钢板墙结构的内力计算和构件设计。3 屈曲约束钢板墙布置对边缘构件受力的影响 在进行框架-两边连接屈曲约束钢板墙结构设计时，对于给定的承载力和刚度需求，如何确定屈曲约束钢板墙的宽度和跨间的布置位置是很重要的问题，不同的墙宽和布置位置都会影响边缘构件的内力和变形。为研究屈曲约束钢板墙在跨间的布置位置对边缘构件（梁）的内力和变形影响规律，以如图4所示的单层单跨框架布置两边连接屈曲约束钢板墙的结构作为算例，跨度l=6 m，屈曲约束钢板墙高h=3 m，梁截面型号为H400×300×12×20，屈曲约束钢板墙宽度分别为框架跨度的1/5，1/4，1/3，1/2和2/3，布置位置为从梁左端[图10（a）]逐渐变化到梁中心[图10（b）]。假定不同宽度屈曲约束

钢板墙的屈服承载力相同（均为1 000 kN），采用图2所示的屈曲约束钢板墙传力模型（仅考虑竖向力分量）计算出不同宽度、不同布置方式的屈曲约束钢板墙达到屈服承载力时所引起的梁内力和转角θ（图11），结果如图12所示。图12中的横坐标从左至右为屈曲约束钢板墙布置位置从梁左端逐渐变化到梁中心，其中0表示屈曲约束钢板墙布置在梁左端[图10（a）]，1表示屈曲约束钢板墙布置在梁中心[图10（b）]。应该注意的是，由于屈曲约束钢板墙宽度不同，图12中的各条曲线在对应相同横坐标时并不表示屈曲约束钢板墙中心处于同一个位置，图12中的曲线仅是为了表达屈曲约束钢板墙位置变化过程中梁内力和变形的变化规律。

由图12可知：

（1）随着屈曲约束钢板墙位置从梁端部到梁中心变化，梁端弯矩均呈单调变化。左端弯矩由负值（逆时针方向）逐渐减小并过渡为正值（顺时针方向）再增大，各条曲线在左端弯矩约等于0的位置重合，而右端弯矩则是逐渐减小。随着屈曲约束钢板墙宽度的增加，梁端弯矩的变化趋于平缓。

（2）随着屈曲约束钢板墙位置从梁端部到梁中心变化，梁端剪力逐渐增大。大约在屈曲约束钢板墙中心距梁端部约为（l+b）/4[或屈曲约束钢板墙左边缘距梁端部为（l-b）/4]时，不同宽度屈曲约束钢板墙产生的梁端剪力接近。随着屈曲约束钢板墙宽度的增加，梁端剪力的变化趋于平缓。

（3）随着屈曲约束钢板墙位置从梁端部到梁中心变化，梁转角逐渐减小。随着屈曲约束钢板墙宽度的增加，梁转角逐渐减小，并且变化趋于平缓。由于梁的转动变形会导致屈曲约束钢板墙也发生转动，从而导致屈曲约束钢板墙的侧移增大，即侧移刚度减小，屈曲约束钢板墙侧移刚度的变化规律与梁转角的变化规律相反。

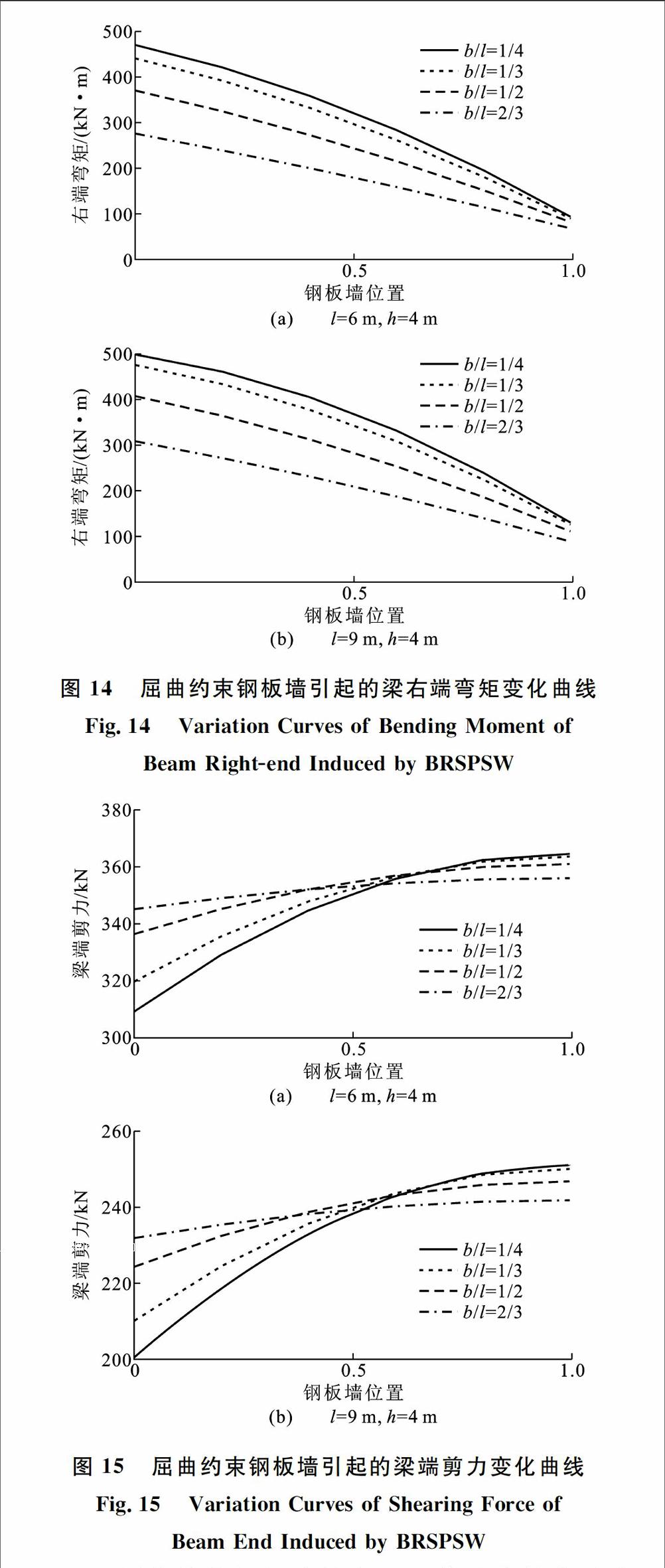
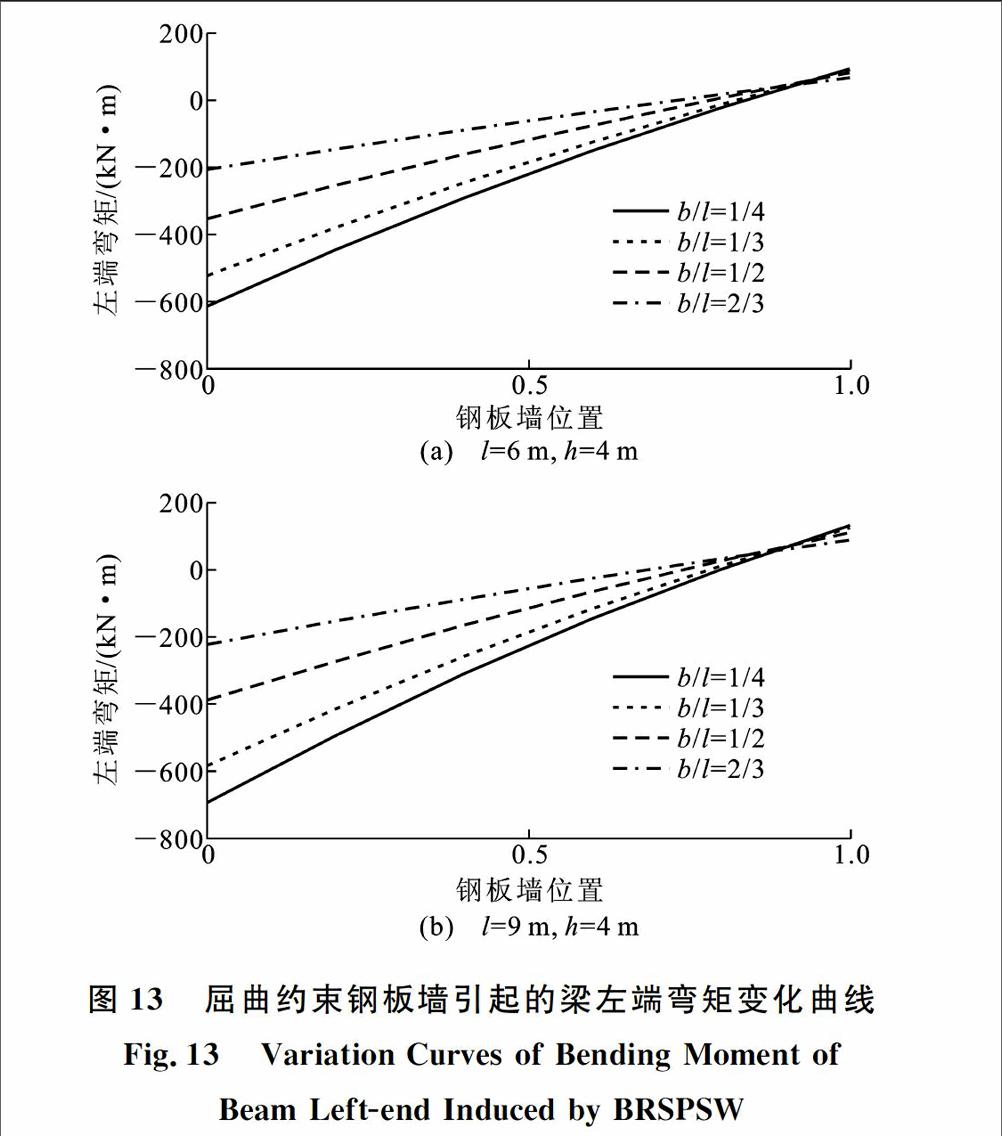
综上所述，从梁端弯矩和侧移刚度的角度来看，屈曲约束钢板墙布置在梁中心比较好；从梁端剪力的角度来看，屈曲约束钢板墙布置在梁端部时梁端剪力最小，当屈曲约束钢板墙宽度大于跨度1/3时，剪力变化趋于平缓，因此布置在中心或其他位置也可以。需要指出的是，当屈曲约束钢板墙宽度增大时内力和变形的变化趋于平缓的原因主要是屈曲约束钢板墙的布置范围变小，而且由于等效支撑的倾角变小，因此屈曲约束钢板墙传给梁的竖向力也有所减小。4 跨度和层高对边缘构件受力规律的影响 除了对l=6 m，h=3 m的结构进行分析研究外，还对l=6 m，h=4 m和l=9 m，h=4 m的结构也进行了分析，以研究跨度和层高对边缘构件受力规律的影响，得到的内力和变形规律见图13～15。从图13～15可以看出，边缘构件的受力规律与图12基本一致。当屈曲约束钢板墙宽度与跨度的比例保持不变时，变化层高或跨度仅影响边缘构件内力和变形的大小，并不影响边缘构件随屈曲约束钢板墙布置位置的变化规律。

5 结 语

（1）提出了两边连接屈曲约束钢板墙边缘构件的内力计算模型，将屈曲约束钢板墙对边缘构件（梁）的分布传力简化为合力点处的集中传力。利用等效支撑模型对所提出的集中传力模型进行了验证，计算得到的梁、柱构件内力与屈曲约束钢板墙结构吻合得较好，特别是控制截面的内力基本一致。

（2）屈曲约束钢板墙的布置宜使边缘构件的内力较小并具有较大的结构刚度。从梁端弯矩和侧移刚度的角度来看，屈曲约束钢板墙宜布置在梁中心，此时梁端弯矩较小，结构刚度较大。从梁端剪力的角度来看，屈曲约束钢板墙宜布置在梁端部，此时梁端剪力最小，当屈曲约束钢板墙宽度大于跨度1/3时，剪力变化趋于平缓，因此布置在中心或其他位置也可以。

（3）边缘构件内力和变形随屈曲约束钢板墙布置位置的变化规律主要受屈曲约束钢板墙宽度与跨度比例的影响。当屈曲约束钢板墙宽度和跨度的比例保持不变时，变化层高或跨度仅影响边缘构件内力和变形的大小，并不影响边缘构件的受力和变形规律。

（4）在进行框架-两边连接屈曲约束钢板墙结构的设计计算时，可采用等效支撑模型代替屈曲约束钢板墙在软件中建模并进行分析。在给定的承载力需求下，屈曲约束钢板墙的宽度宜设计成大于跨度的1/3，并将屈曲约束钢板墙布置在跨度中间。如果屈曲约束钢板墙的宽度只能小于跨度的1/3，则宜布置在靠近梁端部，此时剪力相对最小，虽然梁端弯矩较大，但抗弯设计比抗剪设计容易，这一点在屈曲约束钢板墙边缘构件为混凝土梁时尤为有益。

参考文献：

References：

[1] THORBURN L J，KULAK G L，MONTGOMERY C J.Analysis of Steel Plate Shear Wall：Structural Engineering Report No 107[R].Edmonton：University of Alberta，1983.

[2]TIMLER P A，KULAK G L.Experimental Study of Steel Plate Shear Walls：Structural Engineering Report No 114[R].Edmonton：University of Alberta，1983.

[3]ANSI/AISC 341-10，Seismic Provisions for Structural Steel Buildings[S].

[4] CAN/CSA S16-01，Limit States Design of Steel Structures[S].

[5]PARK H，KWACK J，JEON S.Framed Steel Plate Wall Behavior Under Cyclic Lateral Loading[J].Journal of Structural Engineering，2007，133（3）：378-388.

[6]CHOI I R，PARK H G.Ductility and Energy Dissipation Capacity of Shear-dominated Steel Plate Walls[J].Journal of Structural Engineering，2008，134（9）：1495-1507.

[7]周 明.非加劲与防屈曲钢板剪力墙结构设计方法研究[D].北京：清华大学，2009.

ZHOU Ming.Studies on Design Method of Unstiffened or Buckling-restrained Steel Plate Shear Wall Structures[D].Beijing：Tsinghua University，2009.

[8]孙飞飞，戴成华，高 辉，等.四边连接组合钢板剪力墙简化模型[J].同济大学学报：自然科学版，2009，37（7）：851-856.

SUN Fei-fei，DAI Cheng-hua，GAO Hui，et al.A Simplified Model for Composite Steel Plate Shear Walls[J].Journal of Tongji University：Natural Science，2009，37（7）：851-856.

[9]高 辉，孙飞飞，李国强.组合钢板剪力墙简化计算模型[J].工业建筑，2007，37（增）：588-594.

GAO Hui，SUN Fei-fei，LI Guo-qiang.A Simplified Model for Composite Steel Plate Shear Walls[J].Industrial Constrution，2007，37（S）：588-594.

[10]陆 烨.大高宽比屈曲约束组合墙钢框架束柱体系性能研究[D].上海：同济大学，2009.

LU Ye.Research on the Steel Frame of Bound-column System with Buckling Restrained Steel Plate Shear Wall in Large Aspect Ratio[D].Shanghai：Tongji University，2009.

[11]郭彦林，周 明，董全利，等.三类钢板剪力墙结构试验研究[J].建筑结构学报，2011，32（1）：17-29.

GUO Yan-lin，ZHOU Ming，DONG Quan-li，et al.Experimental Study on Three Types of Steel Plate Shear Walls Under Cyclic Loading[J].Journal of Building Structures，2011，32（1）：17-29.

[12]李国强，刘文洋，陆 烨，等.两边连接屈曲约束钢板剪力墙受力机理与等效支撑模型[J].建筑结构学报，2015，36（4）：33-41.

LI Guo-qiang，LIU Wen-yang，LU Ye，et al.Stressing Mechanism and Equivalent Brace Model for Buckling Restrained Steel Plate Shear Wall with Two-side Connections[J].Journal of Building Structures，2015，36（4）：33-41.