预应力活性粉末混凝土箱梁抗弯性能试验

方志+刘明+郑辉

摘要：为研究预应力活性粉末混凝土（RPC）箱梁的正截面受力性能，进行了2片预应力RPC箱梁的抗弯性能试验，研究了RPC箱梁的受力变形特征以及顶板横向预应力对其抗弯性能的影响。结果表明：预应力RPC箱梁具有良好的变形能力，其极限变形可超过跨径的1/50；RPC箱梁正常使用阶段的裂缝宽度和短期刚度可参照《纤维混凝土结构技术规程》（CECS 38：2004）的相应公式计算，其中的钢纤维影响系数可分别取为0.4和0.2；RPC箱梁顶板内的横向预应力对截面抗弯承载力的影响较小，但会使受压区混凝土的应变分布更加均匀，从而减弱箱梁顶板受压的剪力滞效应并增加构件的延性；试验中对顶板内施加2.95 MPa的横向预压应力（仅为RPC棱柱体抗压强度94 MPa的3.1%）后，可使箱梁受压翼缘的有效分布宽度增加约10%，构件延性指标增加约3%。试验结果验证了提出的预应力RPC箱梁正截面抗裂和抗弯承载力的计算公式。

关键词：活性粉末混凝土；箱梁；抗弯性能；剪力滞效应；裂缝；变形

中图分类号：U448.35 文献标志码：A

0 引 言

活性粉末混凝土（Reactive Powder Concrete，RPC）作为超高性能混凝土（Ultra High Performance Concrete，UHPC）的一种，具有强度高、韧性大和耐久性能优异等特点，且在热养护条件下几乎没有收缩，在长期荷载作用下的徐变也很小（仅为普通混凝土的1/10左右）[1]。RPC的工程应用可望解决普通混凝土桥梁所面临的结构自重过大、跨越能力受限和耐久性不足等问题，其应用研究已引起土木工程界的极大关注并已应用到一些人行桥和中、小跨径的车行桥中[2-3]，在大跨桥梁中的应用研究也已逐步开展[4-6]。此外，混凝土箱梁结构以其良好的空间受力性能在桥梁工程中应用广泛，而RPC箱梁非常适于构成大跨混凝土桥梁的主梁，因此RPC箱梁亦具有良好的应用前景。在大跨混凝土箱梁桥中，除纵向预应力筋外，一般还在腹板和顶板分别配置竖向抗剪和横向抗弯的预应力筋而形成箱梁内的三向预应力体系。顶板内存在的横向预应力对箱梁纵向抗弯性能的影响目前鲜见研究。

文献[7]提出了钢筋RPC梁正截面抗裂计算公式，建议截面抵抗矩塑性影响系数可取为1.65（矩形截面）和1.90（T形截面）；文献[8]进行了3根钢筋RPC矩形截面梁的抗弯性能试验并提出了相应的正截面承载力计算公式，将受压区RPC的应力分布等效为矩形应力图形计算；文献[9]基于有限元分析结果建立了RPC梁的正截面承载力计算公式，将受压区混凝土应力近似为三角形分布；文献[10]对预应力RPC的T形梁进行了试验研究，提出了预应力RPC的T形梁开裂弯矩和极限弯矩的计算方法，并建议预应力RPC的T形梁的塑性系数γ=1.53；文献[11]通过6根钢筋RPC矩形截面梁抗弯性能试验研究，建立了考虑截面受拉区拉应力贡献的正截面承载力计算公式和反映钢筋RPC梁自身受力特点的刚度及裂缝宽度计算方法；文献[12]对铁路预应力RPC箱梁进行了使用荷载下受力性能的试验研究；文献[13]对跨径为24 m的预应力RPC梁进行了试验，梁中除了预应力筋外没有配其他钢筋，其混凝土抗压强度达到了207 MPa，极限挠度达到了480 mm。目前各国学者对RPC梁的正截面受力性能进行了较多研究，但主要针对T形梁和矩形截面梁，对RPC箱梁的研究很少且均未涉及箱梁顶板横向预应力对梁抗弯性能的影响。基于此，本文通过对2片预应力RPC箱梁进行受弯试验，研究预应力RPC箱梁的正截面抗弯性能及横向预应力对其抗弯性能的影响。

1 试验概况

1.1 试件制作

共制作2片截面尺寸相同的预应力RPC箱梁，梁编号分别为A1和A2，截面尺寸如图1所示。梁长5.0 m，计算跨径4.76 m，梁高500 mm，顶板宽600 mm，顶板厚70 mm，腹板厚60 mm，腹板高350 mm，底板宽400 mm，底板厚80 mm。在梁端部设置150 mm厚的横隔板。为研究横向预应力对抗弯性能的影响，试验梁A2跨中纯弯区段顶板布置了8根间距为150 mm的后张横向预应力筋，见图2。

试验梁采用的RPC中水泥、硅灰、石英砂、减水剂的配合比为1.00∶0.25∶1.4∶0.072，水胶比为0.20，钢纤维体积掺量为2%。水泥采用P.O 52.5普通硅酸盐水泥；石英砂粒径为0.4～0.6 mm；采用可溶性树脂型高效减水剂，其掺量（质量分数）为2%，减水率为25%；钢纤维采用镀铜光面平直钢纤维，其直径为（0.16±0.005） mm，长度为（12±1） mm，抗拉强度大于2 000 MPa，体积掺量为2%。试验梁浇筑完成后采用塑料薄膜覆盖其表面，在实验室条件下对其进行自然养护。试验梁浇筑时预留100 mm×100 mm×100 mm的立方体试块和100 mm×100 mm×400 mm的棱柱体试块，用于测

图2 试验梁A2立面及配筋（单位：mm）

Fig.2 Elevation and Reinforcement of Test Beam A2 （Unit：mm）试RPC的抗压强度、劈裂强度和弹性模量，测试结果见表1，其中配筋率包含纵向预应力筋。张拉龄期为50 d，试验龄期为120 d。

试验梁A1底板纵向布置5根直径16 mm的HRB400钢筋及6根Φ15.2预应力钢绞线；顶板纵向布置10根直径10 mm的HRB400钢筋，横向布置间距150 mm、直径10 mm的HRB400钢筋；腹板每侧纵向布置4根间距100 mm、直径8 mm的HRB335钢筋；沿梁长布置间距100 mm、直径12 mm的HRB400箍筋，试验梁配筋情况如图2所示。梁A2除在跨中纯弯区段顶板横向不配置普通钢筋及仅布置8根间距为150 mm、直径16 mm的HRB400钢筋作为横向预应力筋外，其余配筋情况与试验梁A1一致，横向预应力筋两端加工成丝杆以形成螺丝端杆锚具进行锚固。钢筋的力学性能如表2所示。

1.2 应变测点布置

试验梁上布置如图3所示的应变测点。顶板和腹板底部布置的纵向平均应变计（标距为300 mm的引伸仪）用来测量纵向预应力张拉时的应变变化；顶板布置的横向混凝土应变片用来测量横向预应力张拉时的应变变化；跨中截面布置纵向混凝土应变片和纵向、横向平均应变计用来测量试验过程中的应变变化。

1.3 预应力张拉及测试

每片试验梁底部布置6根后张法预应力钢绞线，采用金属波纹管成孔，通过BM-3锚具进行锚固。试验梁浇筑50 d后张拉，采用力传感器测量张拉力并测试张拉过程中各测点应变。纵向预应力筋张拉后进行横向预应力筋张拉，参考目前箱梁桥的工程实际，顶板内的横向预压应力目标值按3 MPa控制。

为保证混凝土预压应力分布均匀，在横向预应力筋两端锚具下布置如图3所示刚度较大的钢垫板。预应力张拉后，采用高性能灌浆料对纵向和横向预应力筋孔道进行灌浆，灌浆时留取70.7 mm×70.7 mm×70.7 mm的立方体试块并进行同条件养护，试验前的强度测试结果如表1所示。试验后，凿开预应力筋管道发现灌浆质量良好。

纵向、横向预应力张拉后、外荷载施加前各测点应变实测结果见表3，记受压为“-”，受拉为“+”。试验梁A1，A2跨中截面上、下缘纵向预应力（由实测应变乘以实测弹性模量得到）分别为2.25，2.71，-10.98，-10.84 MPa；顶板内的横向预应力为-2.95 MPa。

1.4 加载方式与测试内容

试验加载装置如图4所示。两点对称加载，加载点均距跨中400 mm， 每一加载点处千斤顶下设

有分配梁将荷载直接传至腹板，采用力传感器控制加载大小。加载过程中的测试内容为：

（1）挠度测试。在跨中、加载点及支座处布置位移传感器，获取试验梁的荷载-挠度曲线。

（2）裂缝观测。加载过程中对裂缝的发展和宽度进行测量。

（3）应变测试。利用跨中截面顶板粘贴的纵向应变片和纵向、横向平均应变计测试不同位置的应变。

采用分级加载，试验梁开裂前以25 kN为一级加载至近开裂荷载，然后以10 kN为一级加载直至混凝土开裂。梁开裂后，以25 kN为一级加载，每级加载完持荷3 min，接近极限荷载时以3 mm为一级进行位移控制加载，当出现顶板混凝土压碎时认为其达到破坏，随后开始卸载。2 试验结果与分析

2.1 试件破坏形态及裂缝分析

梁A1加载到155 kN时（荷载值为一侧千斤顶下的测力计读数，下文同），在跨中纯弯区段出现竖向裂缝；继续加载，在剪弯区段出现斜裂缝，裂缝宽度和长度均随荷载增大而增加，靠近一侧加载点处的1条竖向裂缝逐渐延伸到翼缘板形成临界裂缝。加载至496.5 kN时，顶板形成不规则的贯通裂缝，顶板混凝土压碎而破坏，试验梁破坏时裂缝形态如图5（a），（b）所示。梁A2加载至157 kN时，在跨中纯弯区段出现竖向裂缝；继续加载，其裂缝开展和荷载变化与试验梁A1相似，当加载至503.9 kN时，顶板处混凝土压碎并在顶板形成贯通的横向裂缝，破坏时裂缝形态如图5（c），（d）所示。横向预应力的施加对试验梁的破坏形态没有明显影响。

试验梁RPC内的钢纤维使裂缝分布密集且裂缝间距较小，梁A1，A2裂缝分布如图6，7所示。弯曲裂缝在纵向钢筋处的裂缝间距约为50 mm，如表4所示。试验梁最大裂缝宽度随荷载的变化如图8所示。相同荷载下，2片试验梁的最大裂缝宽度相近。

式中：ωmax为不考虑钢纤维影响的普通钢筋混凝土受弯构件的最大裂缝宽度，可按照《混凝土结构设计规范》（GB 50010—2010）计算；βcw为裂缝宽度的钢纤维影响系数，宜通过试验确定；λf为钢纤维含量特征值，λf=ρflf/df，ρf为钢纤维体积率，lf为钢纤维长度，df为钢纤维直径或等效直径，本文试验中取λf=1.5。

《纤维混凝土结构技术规程》（CECS 38：2004）中规定当钢纤维混凝土强度等级高于CF45时，对于采用高强度（抗拉强度不小于1 000 MPa）异形钢纤维的受弯构件，可取βcw=0.5。根据试验数据分析结果，对于采用高强度镀铜光面平直钢纤维时的RPC，建议取βcw=0.4，结果比较见图8。

参照式（1），假定平均裂缝间距lfm跟ωfmax有类似的计算公式，即

lfm=lm（1-βflλf）

（2）

式中：lm为不考虑钢纤维影响的普通钢筋混凝土受弯构件的平均裂缝间距，可按《混凝土结构设计规范》（GB 50010—2010）计算；βfl为钢筋钢纤维混凝土构件平均裂缝间距的钢纤维影响系数。

基于试验梁平均裂缝间距的实测结果，对于采用高强度镀铜光面平直钢纤维时的RPC，计算时可取βfl=0.4。

2.2 荷载-挠度曲线

连续采集的试验梁截面荷载-跨中挠度曲线见图9，试验梁破坏点的荷载及挠度见表5。从图9可以看出：在跨中挠度达到其极限变形的约80%之前 ，梁A1，A2的荷载-跨中挠度曲线基本重合，极限

承载力相近。虽然梁A2顶板因横向预应力的施加使其处于双轴受压状态，但施加的2.95 MPa横向预压应力较小，仅为RPC棱柱体抗压强度94 MPa的3.1%，根据文献[14]可知，在此应力比下其双轴抗压强度约为单轴抗压强度的1.05倍，故顶板横向预应力对构件这一过程的受力及截面承载能力的影响不明显。在预应力筋屈服后采用位移控制加载，故顶板处混凝土压碎时（图9中的D1，D2点），荷载突然降低至图9中的E1，E2点，梁A1荷载下降33.2%，挠度增长3.9%；梁A2荷载下降15.6%，挠度增长1.1%，可见横向预应力使梁破坏时的脆性有所改善。对图9中的E1，E2点之后进行卸载。梁A1，A2均具有良好的变形能力，跨中最大挠度（图9中的D1，D2点）分别为98，101.7 mm，均超过梁计算跨径的1/50。

2.2.1 延性分析

试验梁为同时配有预应力筋和非预应力筋的部分预应力混凝土梁，预应力筋和非预应力筋的屈服不可能同步，非预应力筋一般先进入屈服状态。若沿用传统的极限位移与屈服位移之比来定义结构的延性不太明确，因此这里采用Naaman等[15]建议的基于能量的延性指标定义，即

式中：μ为构件的延性指标；Etol为总能量，Etol=Eel+Epl，Eel为弹性能量，Epl为塑性能量，其值可根据图10所示结构的荷载-挠度（P-Δ）曲线所包围的相应部分面积确定。

图10中，P1，P2，P3，Pu和Δ1，Δ2，Δ3，Δu分别为混凝土开裂、普通钢筋屈服、预应力筋屈服和混凝土梁破坏时所对应的荷载及挠度。

由式（3）所确定的梁A1和A2的延性指标分别为3.81和3.92。可见，顶板横向预应力的施加使顶板混凝土的横向变形受到约束而导致梁的延性有所提高，梁A2顶板内施加2.95 MPa的横向预压应力（仅为RPC棱柱体抗压强度94 MPa的3.1%）后，其延性较梁A1提高2.9%。

2.2.2 挠度计算

混凝土开裂前的弹性工作阶段（图9中的OA段），全截面参与工作，取截面的短期抗弯刚度Bfs=EcI0，其中，I0为换算截面惯性矩。

截面开裂到普通钢筋屈服阶段（图9中的AB段），其刚度随弯矩的增大而减小，参照《纤维混凝土结构技术规程》（CECS 38：2004），受拉区开裂后其短期抗弯刚度Bfs可按式（4）计算，即

Bfs=Bs（1+βBλf）

（4）

式中：Bs为不考虑钢纤维影响的普通钢筋混凝土受弯构件的短期刚度，可按《混凝土结构设计规范》（GB 50010—2010）计算；βB为构件短期抗弯刚度的钢纤维影响系数，宜通过试验确定。

基于试验结果，对于采用高强度镀铜光面平直钢纤维时的RPC，可取βB=0.2。

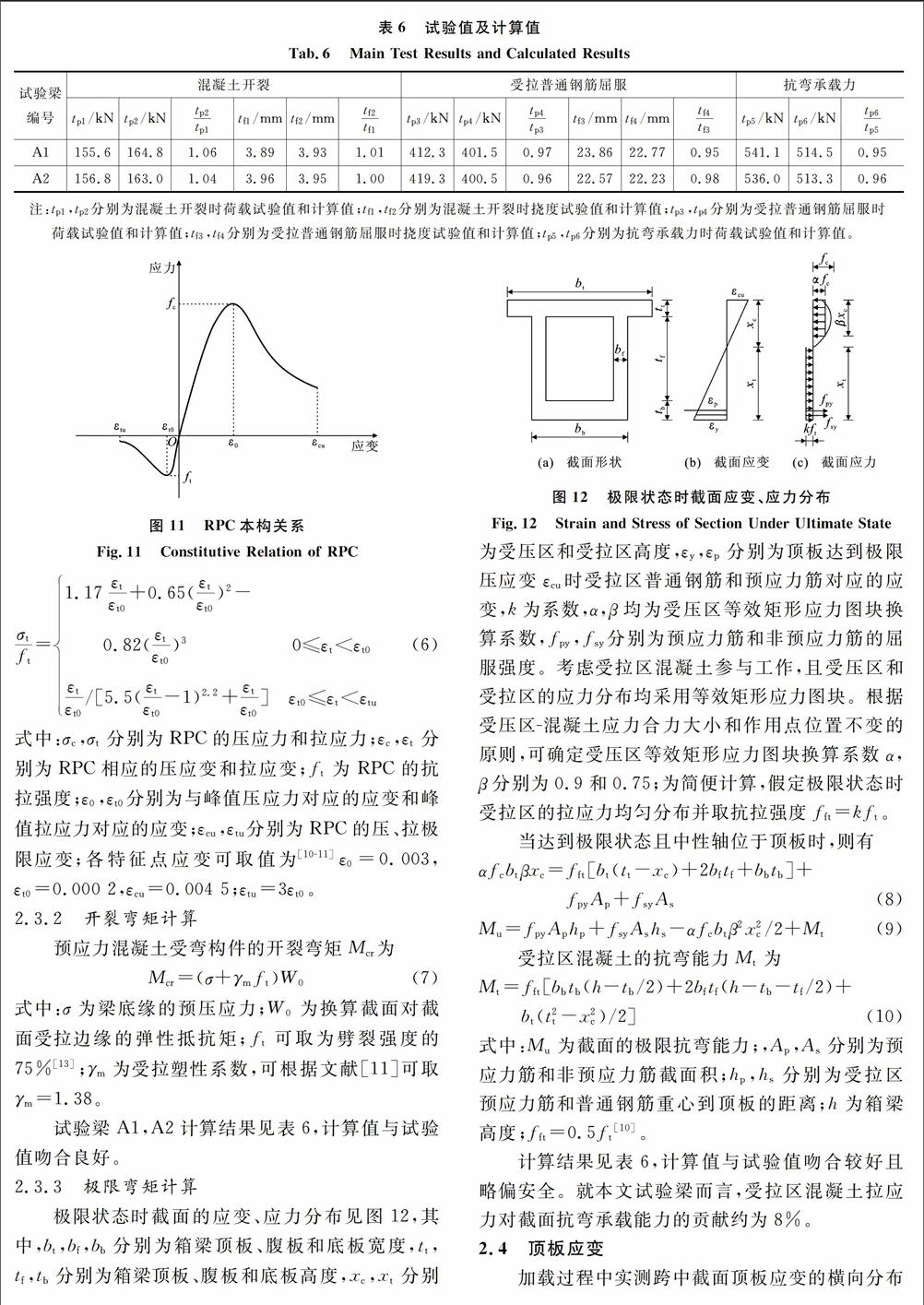
RPC开裂和普通钢筋屈服时的挠度计算结果见表6，计算值与试验值吻合良好。

2.3 开裂弯矩及极限弯矩计算

2.3.1 RPC本构关系

本文采用的RPC受压和受拉时应力-应变关系（图11）分别如式（5），（6）[11]所示，即

荷载试验值和计算值；tf3，tf4分别为受拉普通钢筋屈服时挠度试验值和计算值；tp5，tp6分别为抗弯承载力时荷载试验值和计算值。

式中：σc，σt分别为RPC的压应力和拉应力；εc，εt分别为RPC相应的压应变和拉应变；ft为RPC的抗拉强度；ε0，εt0分别为与峰值压应力对应的应变和峰值拉应力对应的应变；εcu，εtu分别为RPC的压、拉极限应变；各特征点应变可取值为[10-11]ε0=0.003，εt0=0.000 2，εcu=0.004 5；εtu=3εt0。

2.3.2 开裂弯矩计算

预应力混凝土受弯构件的开裂弯矩Mcr为

Mcr=（σ+γmft）W0

（7）

式中：σ为梁底缘的预压应力；W0为换算截面对截面受拉边缘的弹性抵抗矩；ft可取为劈裂强度的75%[13]；γm为受拉塑性系数，可根据文献[11]可取γm=1.38。

试验梁A1，A2计算结果见表6，计算值与试验值吻合良好。

2.3.3 极限弯矩计算

极限状态时截面的应变、应力分布见图12，其中，bt，bf，bb分别为箱梁顶板、腹板和底板宽度，tt，tb分别为箱梁顶板、腹板和底板高度，xc，xt分别为受压区和受拉区高度，εy，εp分别为顶板达到极限压应变εcu时受拉区普通钢筋和预应力筋对应的应变，k为系数，α，β均为受压区等效矩形应力图块换算系数，fpy，fsy分别为预应力筋和非预应力筋的屈服强度。考虑受拉区混凝土参与工作，且受压区和受拉区的应力分布均采用等效矩形应力图块。根据受压区-混凝土应力合力大小和作用点位置不变的原则，可确定受压区等效矩形应力图块换算系数α，β分别为0.9和0.75；为简便计算，假定极限状态时受拉区的拉应力均匀分布并取抗拉强度fft=kft。

当达到极限状态且中性轴位于顶板时，则有

αfcbtβxc=fft[bt（tt-xc）+2bftf+bbtb]+

fpyAp+fsyAs

（8）

Mu=fpyAphp+fsyAshs-αfcbtβ2x2c/2+Mt

（9）

受拉区混凝土的抗弯能力Mt为

Mt=fft[bbtb（h-tb/2）+2bftf（h-tb-tf/2）+

bt（t2t-x2c）/2]

（10）

式中：Mu为截面的极限抗弯能力；，Ap，As分别为预应力筋和非预应力筋截面积；hp，hs分别为受拉区预应力筋和普通钢筋重心到顶板的距离；h为箱梁高度；fft=0.5ft[10]。

计算结果见表6，计算值与试验值吻合较好且略偏安全。就本文试验梁而言，受拉区混凝土拉应力对截面抗弯承载能力的贡献约为8%。

2.4 顶板应变

加载过程中实测跨中截面顶板应变的横向分布如图13所示。由图13可以看出，箱梁顶板内存在较明显的剪力滞效应。

式中：Be为翼缘板的有效分布宽度；B为翼缘板的实际宽度；t为翼缘板的平均厚度；σmax为翼缘与腹板相交处的最大正应力；ρ′f为受压翼缘有效分布宽度系数；z为沿跨长方向的坐标；x为沿横断面宽度方向的坐标。

根据式（5）可知，RPC受压的应力-应变关系将应变分布转化为相应的应力分布后，可计算加载过程中受压翼缘的有效分布宽度系数ρ′f（图14）。由图14可见：荷载在300 kN以内时，梁A1受压翼缘的有效分布宽度系数ρ′f变化较小，其值在0.85左右；荷载超过300 kN以后，受压区混凝土逐渐进入明显的塑性状态并在各测点间发生应力重分布，致使剪力滞效应逐渐减弱，受压翼缘的有效分布宽度系数逐渐增大至极限状态时的0.91；梁A2顶板内因有横向预应力的存在，使得翼缘板内的纵向应变在整个受力过程中沿横向的分布较均匀，剪力滞效应不明显，其受压翼缘的有效分布宽度系数较梁A1的大且基本稳定在0.96左右。这主要是由于梁A2内横向预应力的约束作用对箱梁顶板的纵向正应力有一定的卸载作用所致[16]。

通过梁跨中截面顶板布置的纵向、横向平均应变计所测纵向、横向应变可获得顶板处混凝土的横向变形系数（图15）。由图15可见：受拉普通钢筋屈服前，梁A1的横向变形系数变化较小，其值约为0.16，受拉普通钢筋屈服后，其值逐渐增大至极限状态时的0.25；梁A2的横向变形系数在预应力筋屈服前基本保持在0.10左右，其后逐渐减小至极限状态时的0.06，横向预应力对顶板横向变形的约束明显且随横向变形的发展，约束作用逐渐加强。

3 结 语

（1）预应力RPC箱梁具有良好的变形能力，其极限变形可超过跨径的1/50。

（2）预应力RPC箱梁裂缝密集，平均裂缝间距较小，正常使用阶段的裂缝宽度和短期刚度可参照《纤维混凝土结构技术规程》（CECS 38：2004）中的相应公式计算，其中的钢纤维影响系数βB分别取0.4和0.2。

（3）提出了预应力RPC箱梁正截面抗裂和抗弯承载能力计算公式，计算结果与试验值吻合良好。

（4）箱梁顶板的横向预应力对截面抗弯承载力的影响较小，但会使受压区混凝土的应变分布更加均匀，从而使箱梁顶板受压的剪力滞效应明显减弱并增加构件的延性。

参考文献：

References：

[1] RICHARD P，CHEYTEZY M.Reactive Powder Concrete with High Ductility and 200-800 MPa Compressive Strength[J].ACI Special Publication，1994，144：507-518.

[2]BLAIS P Y，COUTURE M.Precast，Prestressed Pedestrian Bridge-worlds First Reactive Powder Concrete Structure[J].PCI Journal，1999，44（5）：60-71.

[3]BRIAN C，GORDAN C.The Worlds First Ductal Road Bridge Shepherds Gully Creek Bridge，NSW[C]//Concrete Institute of Australia.Proceedings of the 21st Biennial Conference of the Concrete Institute of Australia.Brisbane：Concrete Institute of Australia，2003：1-11.

[4]陈昀明，陈宝春，吴炎海，等.432 m活性粉末混凝土拱桥的设计[J].世界桥梁，2005（1）：1-4，16.

CHEN Yun-ming，CHEN Bao-chun，WU Yan-hai，et al.Design of a 432 m Span Reactive Powder Concrete Arch Bridge[J].World Bridges，2005（1）：1-4，16.

[5]王 飞，方 志.大跨活性粉末混凝土连续刚构桥的性能研究[J].湖南大学学报：自然科学版，2009，36（4）：6-12.

WANG Fei，FANG Zhi.Performance Research on Long-span RPC Concrete Continuous Rigid Frame Bridge[J].Journal of Hunan University：Natural Sciences，2009，36（4）：6-12.

[6]任 亮.基于高性能材料的千米级跨径混凝土斜拉桥力学性能研究[D].长沙：湖南大学，2013.

REN Liang.The Study of Super-long Span Concrete Cable-stayed Bridge Based High Performance Materials[D].Changsha：Hunan University，2013.

[7]万见明，高 日.活性粉末混凝土梁正截面抗裂计算方法[J].建筑结构，2007，37（12）：93-96.

WAN Jian-ming，GAO Ri.Calculating Method of Crack-resistant Capacity of Reactive Powder Concrete Beam[J].Building Structure，2007，37（12）：93-96.

[8]王兆宁.活性粉末混凝土矩形截面配筋梁抗弯性能研究[D].北京：北京交通大学，2008.

WANG Zhao-ning.Research on Flexural Behavior of Reactive Powder Concrete Rectangular Beam with Steel Bars[D].Beijing：Beijing Jiaotong University，2008.

[9]王文雷.RPC预应力梁相关设计参数研究[D].北京：北京交通大学，2006.

WANG Wen-lei.The Research of Design Coefficients About RPC Prestressed Beam[D].Beijing：Beijing Jiaotong University，2006.

[10]杨 剑，方 志.预应力超高性能混凝土梁的受弯性能研究[J].中国公路学报，2009，22（1）：39-46.

YANG Jian，FANG Zhi.Research on Flexural Behaviors of Prestressed Ultra High Performance Concrete Beams[J].China Journal of Highway and Transport，2009，22（1）：39-46.

[11]郑文忠，李 莉，卢姗姗.钢筋活性粉末混凝土简支梁正截面受力性能试验研究[J].建筑结构学报，2011，32（6）：125-134.

ZHENG Wen-zhong，LI Li，LU Shan-shan.Experimental Research on Mechanical Performance of Normal Section of Reinforced Reactive Powder Concrete Beam[J].Journal of Building Structures，2011，32（6）：125-134.

[12]余自若，阎贵平，唐国栋，等.铁路RPC箱梁抗弯性能试验研究[C]//中国土木工程学会.先进纤维混凝土试验·理论·实践——第十届全国纤维混凝土学术会议论文集.北京：中国土木工程学会，2004：89-95.

YU Zi-ruo，YAN Gui-ping，TANG Guo-dong， et al.Experiment Study on Behaviors of Railway RPC Box Girder Bridge Under Flexural Loading[C]//China Civil Engineering Society.Advanced Fiber Reinforced Concrete Test，Theory，Practice — Proceedings of the Tenth National Conference on Fiber Reinforced Concrete.Beijing：China Civil Engineering Society，2004：89-95.

[13]FORTNER B.Materials：FHWA Gives Superior Marks to Concrete Bridge Girder[J].Civil Engineering，2001，71（10）：17.

[14]过镇海，时旭东.钢筋混凝土原理和分析[M].北京：清华大学出版社，2003.

GUO Zhen-hai，SHI Xu-dong.Reinforced Concrete Theory and Analyse[M].Beijing：Tsinghua University Press，2003.

[15]NAAMAN A E，JEONG S M.Structural Ductility of Concrete Beams Prestressed with FRP Tendons[C]//TAERWE L.Non-metallic（FRP） Reinforcement for Concrete Structures.London：Taylor & Francis，Inc.，1995：379-386.

[16]文国华，程翔云.横向预应力对箱梁正应力的影响[J].公路，1997（1）：34-36.

WEN Guo-hua，CHENG Xiang-yun.Effect of Transverse Prestressing on the Normal Stress of Box Girder[J].Highway，1997（1）：34-36.