通过活断层区地铁隧道损伤分析
赵颖+赵亚哥白+郭恩栋+林晓东


摘要:为了深入研究通过活断层区地铁隧道的损伤破坏机理,发现其抗震薄弱部位,采用理论分析、数值模拟和统计回归等方法对逆断层位错作用下隧道衬砌结构的损伤发展变化情况进行了分析,并对减轻隧道震害的影响因素进行了研究。结果表明:建立的地基土-隧道体系整体有限元模型能够很好地模拟逆断层的错动效果;在逆断层位错作用下,衬砌结构的拱顶部位损伤最为严重,结构的损伤程度随着位错量的增加而增大,损伤区域主要集中在活断层附近;在相同逆断层位错作用下,随着覆盖土层厚度的增加,衬砌结构的破坏程度有所减轻;给出的适用于北京地区的衬砌结构抗震薄弱部位估计公式为通过活断层区地铁隧道的抗震设计提供了参考依据;适当增加衬砌厚度可以减轻隧道结构的震害,埋置于较软土质中的隧道结构能够更好地抵抗逆断层位错作用。
关键词:隧道工程;地铁隧道;活断层;拟静力有限元法;损伤分析
中图分类号:U451 文献标志码:A
0 引 言
中国处于活动期的断层分布较广,有许多大中城市均遭遇过强烈地震的袭击,地震发生的频度高、强度大,造成的灾害严重。活断层错动引发的地震不仅能够使覆盖土层地表产生永久的位移,而且还会产生强烈的震动,对于穿越断层的建筑物、地下结构等产生不可修复性的破坏。近年来,许多城市都通过修建地铁来缓解交通压力,很多地铁工程位于高烈度地区,并有可能穿越活断层,所以一旦地震发生则破坏严重,修复困难,还会造成巨大的经济损失和人员伤亡[1]。1952年美国加州克恩郡发生7.6级地震,穿越白狼断层破碎带的4座隧道均遭受到边墙混凝土剥落,产生扭曲变形,地面出现裂缝,泥石流进入洞内等严重破坏。1995年日本阪神发生7.2级地震,建于花岗岩中的总长度为16 km,穿越多条断层的六甲隧道破坏最为严重,拱肩衬砌出现多条裂缝,洞口开裂破损。地铁结构在此次地震中也遭受到巨大损坏,一部分地铁车站立柱被压坏[2]。2008年四川汶川8.0级地震中处于F3和F2断层之间的龙溪隧道以及通过F11-2断层的紫坪铺隧道破坏严重,衬砌开裂、剥落,甚至大面积垮塌[3]。因此,有必要开展通过活断层区的地铁隧道等地下工程结构的抗震研究工作。
众多学者对通过活断层区隧道抗震开展了一系列的研究工作。Lin等[4]通过提升底板试验模拟了逆冲断层作用下位于砂土中的盾构隧道变形破坏特点,并分析了弹性模量和膨胀角对结构的影响,最后采用了数值模拟计算对试验结论进行了验证。刘恺[5]利用有限元分析软件对成兰线穿越断层的隧道进行了抗断层位错研究,结果表明:在相同断层位错作用下,隧道结构的震害程度随着断层倾角的减小而逐渐增大;在相同断层位错作用下,断层破碎带越宽,隧道受到影响的范围也就越大;在断层错动下,坚硬的围岩对隧道变形和受力的影响较软弱围岩更为不利。刘学增等[6]通过模型试验研究了公路隧道在断层倾角为75°的逆断层粘滑错动工况下的反应规律,试验结论给出了受压区、受拉区的范围以及最大拉应变、压应变发生的位置,并指出衬砌以剪切破坏为主。
目前对于通过活断层区隧道抗震方面的研究主要集中在试验和数值模拟方面,研究成果只是得出一些定性的结论,缺乏普遍性,对于隧道结构在断层错动作用下的反应特性、破坏机理研究不够深入,因此难以用于指导工程实践和抗震设计工作。本文采用理论分析、数值模拟和统计回归等方法对地铁隧道在逆断层作用下的地震反应特征及损伤破坏机理进行系统的研究,并建立适用于北京地区且能够较快速、较准确估计出地铁隧道在逆断层位错作用下的抗震薄弱部位的关系式。此外,对于减轻通过活断层区地铁隧道震害的影响因素进行研究,并得出一些对工程有意义的研究结论。
1 跨断层隧道拟静力有限元计算原理
在外荷载作用下考虑阻尼作用结构体系的动力平衡方程为[7]
式中:M为质量矩阵;C为阻尼矩阵;K为结构的整体刚度矩阵;δ为对应于结构之外的固定坐标体系总位移矢量;P(t)为外力矩阵。
由于地震时断层错动导致隧道衬砌的破坏主要是由于土体的永久变形所致,所以在计算活断层作用下隧道衬砌的动力反应时可以忽略加速度和速度的影响,按拟静力方法计算,假定断层错动只是沿一个方向进行,不考虑往复错动和错动速率等因素的影响,将断层错动分为多次较小的位错,逐步作用在基岩上。
在整个计算分析过程中假定隧道衬砌与土体始终保持接触状态且不会发生滑移,以断层错动量作为荷载,通过土体与隧道衬砌之间的非线性接触模型,将荷载传递到衬砌之上,以此来描述由断层错动而引发的隧道衬砌结构的破坏过程。根据拟静力有限元计算原理,结构体系的运动方程可简化为
式中:Ks,Xs,Fs分别为土体单元节点刚度矩阵、位移向量和外力向量;Kt,Xt,Ft分别为隧道衬砌单元节点刚度矩阵、位移向量和外力向量。
土体与隧道衬砌之间的相互作用是通过土层底部施加强制位移来实现的,假定土体与衬砌之间紧密接触,不发生滑移,由方程(2)可求得土体等效荷载分布,根据土体与衬砌的平衡关系可求得接触部分衬砌的等效外荷载,由方程(3)可求得隧道衬砌的位移,通过多次迭代计算求得隧道衬砌的最终位移,从而进行衬砌结构的非线性反应计算。2 本构模型及计算参数的选取
2.1 钢筋混凝土等效材料损伤塑性本构模型
根据应变协调假设和强度等效假设建立钢筋混凝土等效材料损伤塑性本构模型,模型中的钢筋不再单独定义,而是被等效到钢筋混凝土模型中。该模型主要是对ABAQUS有限元软件中给出的损伤塑性模型的拉伸强化-软化阶段的特性进行了完善。下面介绍该模型建立的主要思路[8]。
根据应变协调假设,假定钢筋与混凝土粘结完好,两者的应变相等,即
式中:εs为钢筋应变;εc为混凝土应变;ε为应变。
钢筋和混凝土等效材料的名义应力σ为
式中:SA为钢筋所占的面积比率;σs,σc分别为钢筋、混凝土的应力。
由此可得弹性阶段钢筋混凝土等效材料的弹性模量E为
式中:Es为钢筋的弹性模量;Ec为混凝土的弹性模量。
当钢筋混凝土结构受到拉伸荷载时,混凝土首先达到抗拉强度,根据强度等效假设,假定等效材料的强度与各种组成材料的强度宏观外在表现相同,可得钢筋混凝土等效材料初始屈服强度σy1为
式中:fct为混凝土抗拉强度。
当钢筋混凝土等效材料的应力超过初始屈服强度σy1后,结构所受的荷载主要由钢筋承担,直到钢筋达到屈服荷载fs,此时钢筋混凝土等效材料的最大屈服极限σy2为
图1为钢筋混凝土等效材料的拉伸应力-应变曲线,其中,εy1,εy2分别为钢筋混凝土等效材料初始屈服应变、最大屈服极限应变。假定界面粘结完好,与σy1和σy2对应的应变εy1,εy2可分别按照上述混凝土和钢筋的初始屈服极限及等效材料的弹性模量近似计算,即
本文模型混凝土的强度等级为C50,钢筋的强度等级为HRB335,根据上述的建模思路可计算出等效材料的拉伸应力、非弹性应变。ABAQUS软件中规定,损伤模型以数据系列的形式输入[9],在拉伸应力状态下采用分段线性损伤演化模型,拉伸应力、非弹性应变与损伤值的对应关系见表1。
由于钢筋混凝土的受压特性主要取决于素混凝土,钢筋的影响很小,因此直接采用ABAQUS中提供的具有硬化和软化阶段的压缩损伤塑性模型[10]。压缩应力-应变曲线如图2所示,压缩损伤因子-非弹性应变曲线如图3所示(参阅《混凝土结构设计规范》(GB 50010—2010)中提供的混凝土单轴应力-应变曲线,并根据能量等效原理计算得出损伤因子)。混凝土材料性能指标如表2所示。
2.2 岩土本构模型及计算参数
Mohr-Coulomb破坏和强度准则在岩土工程中的应用十分广泛,传统Mohr-Coulomb模型的屈服面存在的尖角导致塑性流动方向不惟一,从而造成数值计算的繁琐和收敛缓慢。为了避免这些问题,ABAQUS提供的Mohr-Coulomb模型选取连续光滑的流动势函数,其形状在子午面上是双曲线,在π平面上是椭圆形[10]。本文模型中上覆土层采用Mohr-Coulomb模型,基岩、断层破碎带采用线弹性模型,计算参数如表3所示。3 跨断层地铁隧道数值计算模型
3.1 地基土-隧道体系整体模型的建立
以北京地铁7号线工程广渠门内站—广渠门外站区间隧道作为工程背景,建立三维数值分析模型。为了使计算模型更为合理,同时又能提高计算效率,经多次试算发现当模型长度增加到400 m后,在断
层附近一定范围内,衬砌结构的反应很小或不再发生变化。模型宽度的选取是根据目前的经验做法取衬砌结构外径的5~10倍,认为超过5倍之后就可以不用考虑人工边界的影响[11-12]。因此,计算模型长度取为400 m,宽度取为60 m。
模型基本假定如下:根据盾构施工的特点,假定衬砌结构与土体之间的接触部分不发生位移或变形,在整个分析过程中始终保持紧密接触;假定衬砌结构为连续均质模型,按照日本隧道规范建议将其弹性模量折减20%来反映衬砌结构各类接头对其刚度的减弱[13];考虑到计算效率及计算收敛性,将上覆土层简化为单一均质土体。
模型高度为64 m,其中上覆土层厚度为60 m,下部基岩厚度为4 m,断层破碎带为一倾斜的薄弱岩体,其宽度为50 m,均采用ABAQUS中的实体单元C3D20R来模拟。衬砌为圆形单层钢筋混凝土管片结构,内径5.4 m,外径6 m,管片厚度0.3 m,采用ABAQUS中的壳单元S4R来模拟。地基土-隧道体系整体有限元模型如图4所示。
模型下盘底部和右端部以及位于下盘上方覆盖土层右端部施加固定边界;上盘底部和左端部、断层破碎带底部以及位于上盘上方覆盖土层左端部施加x轴方向的位移约束。基于拟静力有限元原理计算断层错动引发隧道衬砌结构的非线性反应,采用分步加载增量法,通过给上盘底部和左端部同时施加y轴正方向和z轴负方向的强制位移来模拟逆断层的错动效果。
3.2 模型验证及算例分析
为了验证所建立有限元模型的合理性,利用ABAQUS软件计算了逆断层作用下基岩上覆土层地表位错量,与利用逆断层下地表位错估计公式[14]的计算结果进行了对比,地表位错估计公式如式(11),(12)所示
式中:DB为基岩位错;M为震级;DV为地表垂直位错;H为基岩上覆土层厚度;α为断层倾角。
表4为逆断层下覆盖土层场地地表位错计算结果对比。通过对比分析可见,估计公式的计算结果略小于采用ABAQUS软件的计算结果,相对误差均不超过12%。由此验证本文所建立的有限元模型能够很好地模拟逆断层的错动效果。
逆断层工况下,基岩的地表垂直位错量DV=1.126 m,水平位错量DH=0.65 m,断层倾角α=60°时,采用拟静力有限元计算方法对隧道衬砌结构的非线性反应进行了数值模拟分析。
图5为逆断层下衬砌结构损伤曲线。从图5可以看出,在逆断层作用下衬砌结构的拱顶部位损伤最为严重,衬砌结构出现损伤的区域主要集中在断层破碎带上方及其附近一定范围内,远离断层处结构损伤值为0,说明结构完好无损。这与震害调查中所得到的“隧道在断层错动下的损伤破坏只发生在活断层附近的一定范围内”相吻合。这也进一步验证了本文所建立有限元模型的正确性。
4 结果分析
损伤作为内变量是逐渐发展的,损伤指标是描述结构或构件受损伤程度的变量,为单值增函数,并且具有积累性,可以反映结构的最大反应以及荷载的往复作用。为了使人们对损伤状况有直接概念,损伤指标一般被设定在0~1之间,0表示结构完好,1表示结构倒塌。基于拟静力有限元法,利用损伤指标研究了隧道衬砌结构在逆断层位错作用下的损伤破坏机理,给出了衬砌结构抗震的薄弱部位。
4.1 逆断层下隧道结构损伤分析
由于逆断层主要由水平挤压作用而形成,所以在逆断层作用下,隧道衬砌结构主要表现为挤压型破坏,受压损伤较为严重,故在以下的分析中主要研究隧道衬砌结构受压损伤的非线性行为。在钢筋混凝土受压本构模型中,结构在达到初始屈服应力前,定义为结构的损伤值Dc=0时结构处于安全状态。结构的损伤值Dc>0时结构开始出现损伤破坏,且损伤值越大,结构的破坏程度越严重。计算分析了断层倾角α分别为30°,45°,60°,70°,80°的情况,并且考虑了逆断层位错量(垂直位错量DV和水平位错量DH)、基岩上覆土层厚度H对衬砌结构反应的影响。
图6为逆断层作用下隧道结构损伤立面图。隧道结构的损伤区域主要位于断层错动迹线的两侧,损伤区域长度LD为上盘损伤长度a与下盘损伤长度b的和,即LD=a+b,损伤区间为(-a,b)。
表5~9分别为断层倾角α=30°,45°,60°,70°,80°时逆断层作用下隧道结构损伤情况,其中S为衬砌结构损伤最严重处距断层错动迹线的距离,S<0表示上盘距断层错动迹线的距离,S=0表示断层错动迹线与隧道相交处,S>0表示下盘距断层错动迹线的距离。
从表5~9可以看出:在相同断层倾角、相同土层厚度下,随着逆断层位错量的增加,衬砌结构的损
伤值逐渐增大,损伤区域范围也逐渐向两侧延伸扩展,当位错量增加到一定程度后,衬砌结构的损伤区域长度不再变化;在相同逆断层位错量情况下,随着上覆土层厚度的增加,衬砌结构的损伤值呈减小趋势,这说明增加基岩上覆土层厚度能够减轻衬砌结构的破损程度;当土层厚度一定时,随着断层倾角的增大,衬砌结构出现损伤区域的最终长度逐渐减小。在基岩沿断层面的错动量相同的情况下,断层倾角增大使得断层位错的垂直分量增大,水平分量减小,从而使衬砌结构受到的水平挤压作用相对减小。可见,逆断层作用下水平挤压作用对衬砌结构产生的损伤范围影响较大。
对表5~9中的数据进行多元回归分析,可以拟合为如下关系式
LD=0.617H-2.52DV+6.524DH+
109.468,R2=0.741
(13)
式中:R2为判定系数。
损伤长度a,b分别为
a=0.553H-35.31 DV+
47.294 DH+25.592,R2=0.75
(14)
b=LD-a
(15)
隧道衬砌结构损伤最严重处距断层错动迹线的距离S为
S=140.181DVD2V+D2H-0.169H-
63.398,R2=0.878
(16)
在能够预测活断层位错量的情况下,通过公式(13)~(16)可判断出适用于北京地区的穿越活断层的埋地隧道在逆断层作用下的抗震薄弱部位,公式中考虑了基岩上覆土层厚度的影响,为通过活断层区地铁隧道的合理设计提供了参考。
4.2 逆断层作用下临界覆盖土层厚度估计
在相同逆断层位错作用下,随着基岩上覆土层厚度的增加,隧道衬砌结构的损伤值逐渐减小,当衬砌结构的损伤值趋近于0时所对应的土层厚度定义为临界覆盖土层厚度HC。通过计算得到了不同断层倾角α下临界覆盖土层厚度与逆断层位错量的关系,如表10所示。
对表10中的数据进行回归分析,可不考虑活断层错动的影响,临界覆盖土层厚度HC与逆断层位错量(DV,DH)之间可以拟合为如下关系式
HC=99.5DV+91.264DH+
4.743,R2=0.95
(17)
当基岩上覆土层厚度H≥HC时,可以不考虑逆断层断裂对埋地隧道的影响。这说明基岩上覆土体对逆断层错动量具有一定的吸收作用,土层厚度足够大时逆断层错动不会造成隧道衬砌结构的破坏。该公式能够为北京地区活动断裂地震安全性评估工作提供参考依据。5 减轻隧道震害影响因素分析
地铁隧道在断层位错作用下随其周围的土体共同运动,结构自身的抗震能力、周围土层性质是决定结构抗震安全性的关键因素。因此,主要从衬砌厚度和土层性质2个方面对逆断层作用下地铁隧道震害的影响因素进行了研究。
5.1 衬砌厚度
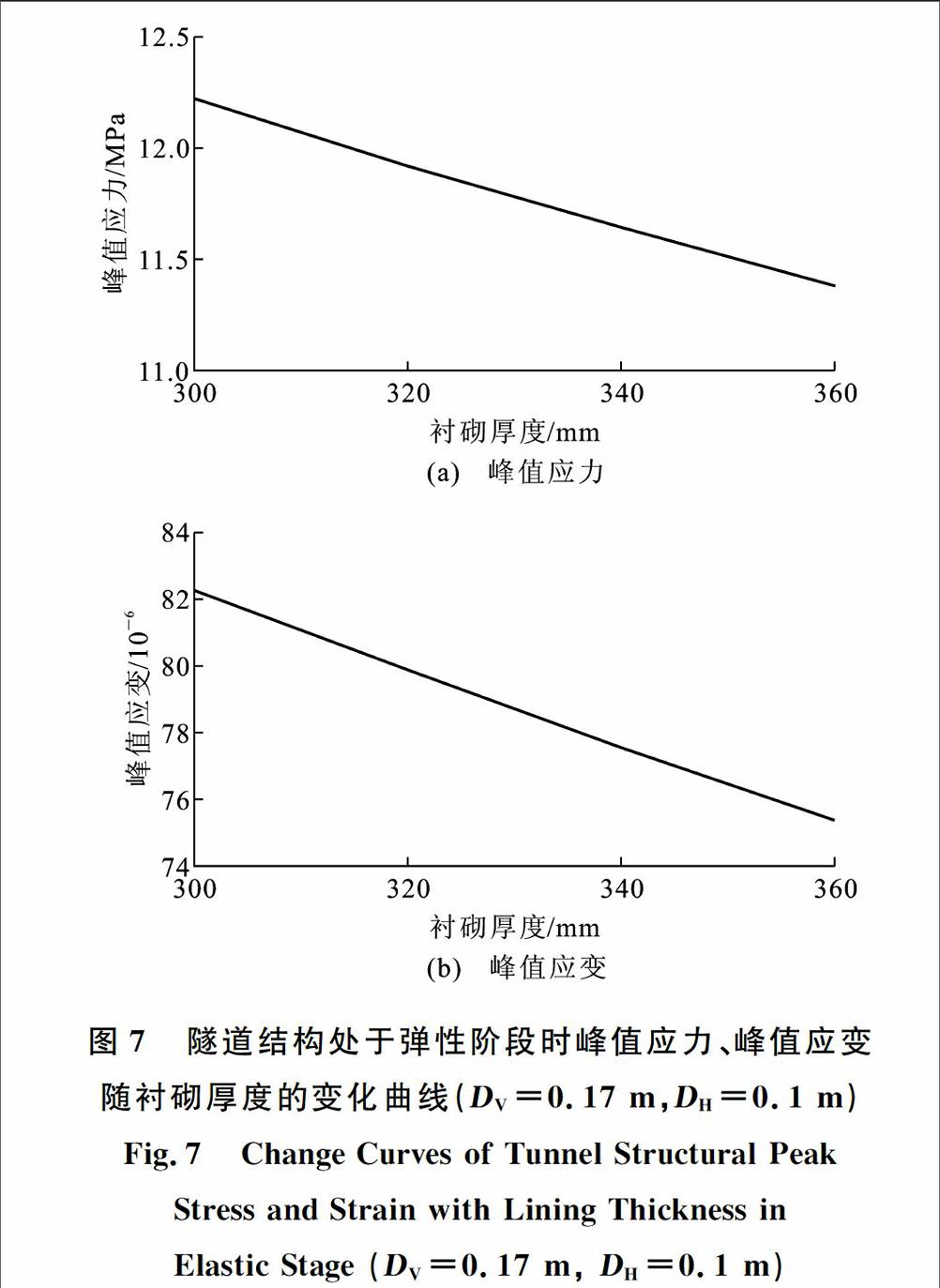
《地铁设计规范》(GB 50157—2003)中对装配式衬砌构造做了如下规定:衬砌厚度应根据隧道直径、埋深、工程地质及水文地质条件、使用阶段及施工阶段的荷载情况等确定,宜为隧道外轮廓直径的0.05倍~0.06倍。本文研究取衬砌厚度分别为300,320,340,360 mm进行分析。图7为逆断层作用下隧道结构处于弹性阶段时峰值应力、峰值应变随衬砌厚度的变化曲线(DV=0.17 m,DH=0.1 m)。从图7可以看出,在逆断层位错量较小的情况下,隧道结构处于弹性阶段,此时的峰值应力、峰值应变均随衬砌厚度的增加而减小。
效塑性应变峰值随衬砌厚度的变化曲线(DV=1.04 m,DH=0.6 m)。从图8可以看出,在逆断层位错量较大的情况下,隧道结构开始出现损伤破坏,隧道结构的最大损伤值和等效塑性应变峰值均随着衬砌厚度的增加而减小。
通过以上分析可知,对于跨越活断层的隧道适当增加衬砌厚度可以减轻结构的震害。这是因为衬砌厚度的增加使得隧道横截面面积增大,从而增大了隧道的刚度,所以结构的反应减小。
5.2 土层性质
取基岩上覆土层分别为粘土、粉质粘土和粉土3种土质进行分析,土体计算参数如表11所示。图9为逆断层作用下隧道结构处于弹性阶段时峰值应力、峰值应变随土质的变化(DV=0.17 m,DH=0.1 m)。从图9可以看出,在逆断层位错量较小的情况下,隧道结构处于弹性阶段,随着土质变软,隧道结构产生的峰值应力、峰值应变逐渐减小。
图10为逆断层作用下隧道结构最大损伤值、等效塑性应变峰值随土质的变化曲线(DV=1.04 m,DH=0.6 m)。从图10可以看出,在逆断层位错量较大的情况下,隧道结构开始出现损伤破坏,隧道结构的最大损伤值和等效塑性应变峰值均随着土质的变软而减小。
通过以上分析可以看出,埋置于较软土质中的隧道结构能够更好地抵抗逆断层位错作用。这是因为随着土质的变软,土体对于隧道结构的约束力逐渐减弱,所以埋置在较硬土体中的隧道结构产生的震害较大。6 结 语
(1)基于拟静力弹塑性有限元理论,建立了地基土-隧道体系整体有限元分析模型,并对模型进行了初步验证,结果表明该有限元模型能够很好地模拟逆断层的错动效果。
(2)通过在数值计算模型中嵌入合理的损伤塑性本构模型,利用损伤指标对隧道衬砌结构在逆断层位错作用下的损伤破坏机理进行了系统的研究,结果表明:衬砌结构出现损伤的区域主要发生在断层破碎带上方及其附近一定范围内,离断层较远处结构完好,结构拱顶部位最先出现损伤且损伤最为严重;在相同条件下,随着逆断层位错量的增加,衬砌结构的损伤值逐渐增大,损伤区域范围也逐渐向两侧延伸扩展,当位错量增加到一定程度后,衬砌结构的损伤区域长度不再变化;在相同逆断层位错量情况下,增加基岩上覆土层厚度能够减轻衬砌结构的破损程度;逆断层作用下水平挤压作用对衬砌结构产生的损伤区域范围影响较大。
(3)根据大量的数值计算结果,利用统计回归方法建立了适用于北京地区且能够判断地铁隧道在逆断层位错作用下出现的损伤区域以及损伤破坏最严重位置的关系式,通过回归分析拟合了可不考虑逆断层影响的临界覆盖土层厚度与断层位错量之间的关系式,为通过活断层区地铁隧道的安全性评价提供了参考依据。
(4)主要从衬砌结构自身特性和周围土层性质2个方面对逆断层作用下减轻地铁隧道震害的影响因素进行了研究,为穿越活断层地铁隧道的抗震设计提供了一定的指导。研究结果指出:适当增加衬砌厚度可以减轻隧道结构的震害;埋置于较软土质中的隧道结构能够更好地抵抗逆断层位错作用。
参考文献:
References:
[1] 刘晶波,李 彬.地铁地下结构抗震分析及设计中的几个关键问题[J].土木工程学报,2006,39(6):106-110.
LIU Jing-bo,LI Bin.Issues on the Seismic Analysis and Design of Subway Structures[J].China Civil Engineering Journal,2006,39(6):106-110.
[2]耿 平,吴 川,唐金良,等.穿越断层破碎带隧道动力响应特性分析[J].岩土力学与工程学报,2012,31(7):1406-1413.
GENG Ping,WU Chuan,TANG Jin-liang,et al.Analysis of Dynamic Response Properties for Tunnel Through Fault Fracture Zone[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(7):1406-1413.
[3]李宏男,肖诗云,霍林生.汶川地震震害调查与启示[J].建筑结构学报,2008,29(4):10-19.
LI Hong-nan,XIAO Shi-yun,HUO Lin-sheng.Damage Investigation and Analysis of Engineering Structures in the Wenchuan Earthquake[J].Journal of Building Structures,2008,29(4):10-19.
[4]LIN M L,CHUNG C F,JENG F S,et al.The Deformation of Overburden Soil Induced by Thrust Faulting and Its Impact on Underground Tunnels[J].Engineering Geology,2007,92(3/4):110-132.
[5]刘 恺.成兰线跨断层隧道的错动破坏机理研究及地震动力响应分析[D].北京:北京交通大学,2011.
LIU Kai.Study on the Failure Mechanism Under Fault Movement and Seismic Dynamic Response of the Chenglan Across-fault Tunnel[D].Beijing:Beijing Jiaotong University,2011.
[6]刘学增,林亮伦.75°倾角逆断层黏滑错动对公路隧道影响的模型试验研究[J].岩土力学与工程学报,2011,30(12):2523-2530.
LIU Xue-zeng,LIN Liang-lun.Research on Model Experiment of Effect of Thrust Fault with 75° Dip Angle Stick-slip Dislocation on Highway Tunnel[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(12):2523-2530.
[7]胡聿贤.地震工程学[M].北京:地震出版社,1988.
HU Yu-xian.Earthquake Engineering[M].Beijing:Seismological Press,1988.
[8]沈新普,王琛元,周 琳.一个钢筋混凝土损伤塑性本构模型及工程应用[J].工程力学,2007,24(9):122-128.
SHEN Xin-pu,WANG Chen-yuan,ZHOU Lin.A Damage Plastic Constitutive Model for Reinforced Concrete and Its Engineering Application[J].Engineering Mechanics,2007,24(9):122-128.
[9]Hibbitt,Karlsson & Sorensen,Inc.ABAQUS Standard Users Manual:ABAQUS 6.5 Theory Manual[M].Waverley:Hibbitt,Karlsson & Sorensen,Inc,2005.
[10]王金昌,陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006.
WANG Jin-chang,CHEN Ye-kai.Application of ABAQUS in Civil Engineering[M].Hangzhou:Zhejiang University Press,2006.
[11]张 伟.大直径盾构隧道结构地震响应及减震措施研究[D].武汉:中国科学院武汉岩土力学研究所,2009.
ZHANG Wei.Study on Seismic Responses and Vibration-absorption Measures for Large-diameter Shield Tunnel[D].Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2009.
[12]吴 波,高 波,索晓明,等.城市地铁小间距隧道施工性态的力学模拟与分析[J].中国公路学报,2005,18(3):84-89.
WU Bo,GAO Bo,SUO Xiao-ming,et al.Mechanical Simulation and Analysis of Construction Behavior of Urban Metro Tunnelling with Small Interval[J].China Journal of Highway and Transport,2005,18(3):84-89.
[13]日本土木学会.隧道标准规范(盾构篇)及解说[M].朱 伟,译.北京:中国建筑工业出版社,2001.
Japans Civil Society.Shield Tunnel Standard Specification and Explanation[M].Translated by ZHU Wei.Beijing:China Architecture & Building Press,2001.
[14]赵 颖,郭恩栋,王 琼,等.走滑断层地震地表断裂位错估计方法研究[J].岩土力学,2013,34(5):1403-1408.
ZHAO Ying,GUO En-dong,WANG Qiong,et al.Estimate Method of Dislocation to Seismic Surface Rupture Under Strike-slip Fault[J].Rock and Soil Mechanics,2013,34(5):1403-1408.

