几何直观在线性代数课堂教学中的应用
张鹏鸽+高淑萍+马建荣
摘要:线性代数课程特点使得其课堂教学一直以来都是教学中的难点和重点,本文从几何直观的角度对课程中行列式和线性相关性理论进行讨论,主要是通过几何直观的思想引导学生,帮助学生理解和掌握这部分内容,使得课堂效果得到大幅提高,并提升教师在线性代数课堂教学中和学生的互动关系,激发学生对线性代数的学习兴趣,更好地落实素质教育在高校中的普及,有助于提高学生的综合素质。
关键词:几何直观;行列式;线性相关与线性无关;秩
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2015)16-0199-02
针对线性代数课程的特点以及几大模块的教学安排,本文重点介绍几何直观在线性代数课堂教学中的应用,使得学生豁然开朗,甚至是醍醐灌顶的感觉。正如中国当代数学家徐利治说:“无论是从事数学教学或研究,我是喜欢直观的。学习一条数学定理及其证明,只有当我能把定理的直观含义和证明的直观思路弄明白了,我才认为真正懂了。”
线性代数是理工、经管类等大学生的一门重要的数学基础课,是学习后续课程不可缺少的工具。我校陈怀琛教授早在2008年全国大学数学论坛报告中指出,线性代数的教学对后续课程的影响非常大,仅机械和电子专业在大学前三年中就有十多门课会用到线性代数的知识,可见提高线性代数课堂教学的重要性是不言而喻的。有人说得好:“开设线性代数课程的目的,不仅是要教给学生一些有用的运算工具和算法,而且要注意提高学生在空间想象、抽象思维、逻辑推理和数学表述等方面的能力,帮助学生构建起崭新的思维方式,为他们的后续课程及进一步深造打好基础。”
从教多年以来,笔者得知学生对线性代数课程的普遍反映就是:抽象,难学,概念、定理多,证明、推理难,尤其是好多概念来得突然,不知所云。为了解决学生面临的这些问题,作者总结了多年的教学经验,重点从几何直观的角度给出线性代数课程中两个抽象概念的几何背景,有助于学生理解和掌握相关知识,并提高了线性代数课堂教学的效果。下面针对该课程中这两个概念做详细讨论。
一、行列式的几何意义
线性代数的主线就是求解线性方程组,矩阵是求解方程组的一大重要工具,而行列式则用来解决一类特殊的方程组,在引入二元一次线性方程组时,提出了行列式的概念,在此我们给出二阶、三阶行列式的几何意义帮助学生理解掌握n阶行列式的意义。
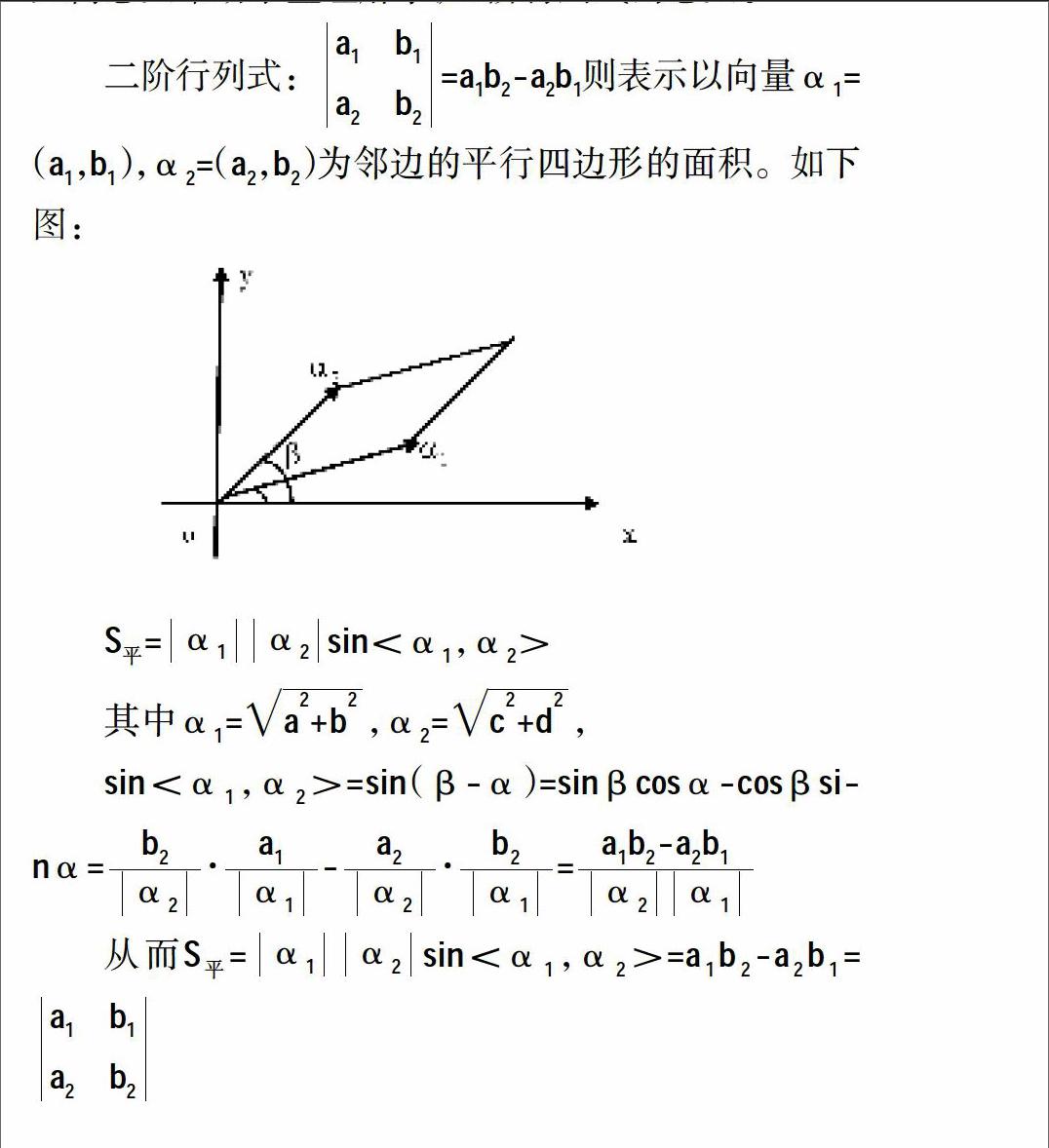
二阶行列式:a■ b■a■ b■=a■b■-a■b■则表示以向量α■=(a■,b■),α■=(a■,b■)为邻边的平行四边形的面积。如下图:
S■=α■α■sin<α■,α■>
其中α■=■,α■=■,
sin<α■,α■>=sin(β-α)=sinβcosα-cosβsinα=■·■-■·■=■
从而S■=α■α■sin<α■,α■>=a■b■-a■b■=a■ b■a■ b■
三阶行列式a■ b■ c■a■ b■ c■a■ b■ c■则表示由行向量或列向量所张成的平行六面体的体积,这一结论可以从两个向量张成的平行四边形推出。如下图所示:
由两个向量α■、α■张成的平行四边形Aα■Bα■,面积S为α■、α■构成的行列式,沿着第三个向量α■会生长出无数个平行于原四边形的新平行四边形,直到α■的末端。显然,所有的这些平行四边形构成一个以向量α■、α■、α■为棱的平行六面体,这些四边形的面积叠加起来正是平行六面体的体积。于是,行列式的几何意义可以解释为:行列式中行或者列向量所构成的超平行多面体的有向面积或有向体积。
二、向量组线性相关性的几何意义
大家都知道向量组的线性相关性是线性代数课程的重点和难点,学生普遍难理解这部分内容的意义,比如相关与无关、极大线性无关组、线性空间的基等概念。课堂上通过几何直观的思想解释线性相关和线性无关的概念,便于学生理解。抽象的东西,学生往往难以理解和掌握,而直观的几何图形往往更容易让人找到学习的切入点,从而更好地掌握相关知识。
向量组中若有一个向量可以由其余向量线性表示,则称这组向量线性相关,否则称其线性无关。在二维平面上,如果两个向量线性相关,则这两个向量一定在一条直线上,方向相同或相反,反之亦成立。这时可以给学生解释:因为在一条直线上的所有向量中两个向量都具有倍数关系,即β=kα,所有向量都线性相关,而不在一条直线上的两个向量一定线性无关(反证法易得矛盾)。在三维空间中,若考虑两个向量的线性相关性,则与平面上共线或不共线的情形相同,若考虑三个或三个以上的向量组的线性相关性时,以三个向量α、β、γ为例,根据定义线性相关是指其中有一个向量可以由其余向量线性表示,不妨设γ=k■α+k■β,当α与β共线时,α、β、γ共线,当α与β不共线时,α与β可以张成一平面,则γ就落在这一平面上,即α、β、γ共面;反之亦成立。显然,不共面或不共线的三维向量组一定线性无关。
从几何意义上讲,在一个向量组里,若有多个向量在同一条直线上,那么这些向量中只需要一个非零向量做代表就可以了,直线上其余向量均可由这一个非零向量表示了,而且这一非零向量选法不唯一;进而,如果向量组中是由多个向量构成且位于一个平面上,那么只要找两个非零非共线的向量做代表就可以了,其余向量就可以用这两个非零非共线的向量表示了。如果向量组中是由多个向量构成且位于一个立体空间中,那么只要找三个非零非共线非共面的向量做代表就可以了,其余向量就可以用这三个非零非共线非共面的向量表示了。
于是n维向量组就可以通过几何筛选得到一个极大线性无关组。学生就可以理解极大线性无关组就是这样一组向量:从原来一组向量中挑出一部分向量组成一个新的向量组,这个新的向量组在某种意义下可以代表原来的向量组,同时这个新向量组很纯净,没有躲在后面滥竽充数的向量,多余的向量都被剔出去了,向量相互独立,谁也不代表,谁也不被代表,这些构成的向量组中向量的个数就是向量组的秩了。实质上,这样向量组就原向量组的一极大线性无关组或是构成向量空间的一组基,极大线性无关组中所含向量的个数即为原向量组的秩或者空间的维数,秩和维数均为不变量。这样学生理解起来就容易多了,而且清楚了极大线性无关组和秩的意义,接下来讲到线性方程组解的结构时学生就非常能理解为何要找一组基础解系来表示全部解。
总结教学经验得到:若将线性代数中抽象概念几何化,学生会很容易掌握,同时课堂教学效果也大幅提高,最主要的是教会了学生一种借助几何直观分析问题、思考问题、解决问题的科学方法,对后续课程的学习将大有益处。
参考文献:
[1]沈雁.线性代数教学中直观性应用的时间与思考[J].数学教育学报,2010.
[2]成琨,任永泰.提高线性代数课堂教学有效性方法的探讨[J].大学教育,2013,(5).
[3]同济大学数学教研室.线性代数[M].北京:高等教育出版社,1998.
[4]刘三阳,马建荣,杨国平.线性代数[M].北京:高等教育出版社,2009.
[5]姜红燕.几何思想融入向量组线性相关性的教学探讨[J].宜宾学院学报,2013.
[6]钱林.计算机辅助线性代数教学浅议[J].江苏教育学院学报(自然科学版),2006,(04).
[7]王健,郭明普.线性代数教学中加强几何直观教学的意义[J].新乡师范高等专科学校学报,2003,(02).endprint