火星探测器进入段预测校正制导方法
夏元清,沈刚辉,孙浩然,周鎏宇
(北京理工大学自动化学院,北京100081)
火星探测器进入段预测校正制导方法
夏元清,沈刚辉,孙浩然,周鎏宇
(北京理工大学自动化学院,北京100081)
根据美国宇航局的计划,未来火星探测任务的要求是能确保在高精度和高海拔的火星表面着陆,而进入段所使用的制导方法是探测器能够精确着陆的关键。文章首先介绍了两种进入段制导算法——标称轨迹算法和预测校正算法,通过比较得出预测校正算法对于初始扰动的敏感性较低,但需要有较高的在线计算能力;其次,文章对于预测校正中的横向控制,纵向控制算法和航向调整算法进行了详细介绍,同时提出一种通过增加检测点的改进预测校正算法;最后对算法进行软件仿真,仿真结果表明:这种进入段预测校正制导算法在有很高不确定性的情况下仍然能体现出可靠性和鲁棒性。
进入段制导方法;预测校正;横向控制;航向调整
0 引 言
随着20世纪60多代,前苏联向火星发射第一枚探测器起,人类对于火星的探索就从来没有停止过。进入21世纪后,随着航空航天技术的不断发展与进步,深空探测作为一个国家综合实力和科学技术发展水平的重要标志,引起了世界各国的广泛关注。火星由于紧靠地球,其自然环境相比于其他行星更接近于地球。因此,人类多少年来一直对火星探测充满兴趣。火星探测作为深空探测的重要组成部分已经成为现在和未来一段时间内,人类进行深空探索的热点之一[12]。
由于火星具有大气层,因而要实现火星表面软着陆就必须经历大气进入、下降以及最终着陆段(entry,descent,landing,EDL)三个过程。探测器的进入段一般开始于着陆器接触火星大气层,结束于降落伞完全打开。整个过程仅利用火星大气进行减速,消耗掉99%的动能,将探测器速度减到合适的开伞条件,期间经历制动过载、动压峰值同时产生大量的气动热,是整个EDL过程中气动环境最恶劣,也是整个过程中最重要的阶段[3]。另外,由于火星大气密度非常稀薄,仅为地球的1%,探测器仅依靠自身的气动外形进行减速,因而合适的气动外形是确保火星探测器安全通过进入段的高速高温飞行区,并最终实现在火星表面软着陆的重要保障[4]。
目前,航天器大气进入段的制导算法大体分为两类:标称轨迹制导法和预测校正制导法。标称轨迹制导法,在获取飞行器进入时刻状态参数以及期望开伞点的信息后,设计一条满足过程约束(动压、热量、速度等)和终端约束(经纬度、速度、高度、压力等)的标称轨迹,制导系统通过获取飞行时刻的状态参数与标称轨迹参数的误差信号,通过反馈控制律给出控制信号,从而让飞行器尽可能地沿着已设计的标称轨迹飞行,达到指定的开伞点[5];预测校正制导算法,在每个制导周期开始,根据当前的状态参数以及期望的落点位置,设计一条满足约束条件并能到达期望位置的飞行轨迹,进而给出控制信号,实现对飞行器飞行轨迹的控制,达到期望开伞点。预测校正制导算法不需要设计并跟踪标称轨迹,而是在每段采样时间间隔内实时设计能满足各项要求的飞行轨迹,需要进行在线的预测和校正,因此在线计算量较大。
本文主要介绍一种完整的预测校正制导算法,用来对飞行器的进入段进行制导控制。该预测校正算法包括纵向的预测校正、横向滚转角的翻转策略。最后将航路点制导算法与传统的预测校正算法相结合,提出新的改进制导算法—新型航路点分段预测校正制导算法。此外,算法的仿真结果验证了传统预测校正算法和航路点分段预测校正算法的有效性和鲁棒性。
1 火星进入段动力学模型
根据文献[6]和文献[7],火星进入段的大气动力学模型可以表示为

其中:L和D分别为探测器在进入火星大气阶段所受到的空气升力加速度和阻力加速度,它们与探测器的飞行速度,有效横截面积,火星大气密度等因素相关[7];θ为火星的经度;ϕ为火星的纬度;V为探测器在火星大气中运行时的速度;r为探测器质心到火星质心之间的距离;ψ表示探测器运行的航向角,其表示的意义为速度在水平面的投影与正东方向的夹角;γ表示探测器的飞行路径角;σ称为滚转倾侧角,表示探测器所受的升力与竖直方向的夹角,倾侧角右偏定义为正方向。
2 火星大气进入段制导控制算法
如引文所述,进入段的制导控制方法主要分为两种:一种是标称轨迹跟踪控制;另一种是预测校正算法。两种算法的特点如下所示:标称轨迹跟踪控制方法不需要很精确的模型,可以在线或离线设计标称轨迹,不要求很高的在线计算能力,但是其缺点是对初始条件具有较高的敏感性;预测校正算法可以有效克服初始扰动对制导控制精度的影响,但是其却有在线计算量大、计算时间较长的缺点。
2.1 标称轨迹跟踪控制方法
“阿波罗”任务首次采用标称轨迹制导法[6]。目前火星探测器的大气进入段轨迹规划基本都源自“阿波罗”任务,跟踪控制律的设计主要采用反馈线性化的方法来设计。标称轨迹制导法对模型的依赖较小,也不需要很高的在线计算能力,对机载计算机的要求较小,但是其对初始条件具有很高的敏感性,当初始条件的误差达到一定程度时,将不能实现对标称轨迹的跟踪,导致很大的落点误差。Xia Y等(2014)[7]提出了一种方法将自抗扰控制算法(active disturbance rejection controller,ADRC)作为反馈控制律应用到火星进入段制导问题当中,通过仿真显示了该方法相比于传统PID算法具有更好的性能。
2.2 预测校正算法
与上述的标称轨迹制导法相比预测校正制导法则正好相反,其具有对初始误差不敏感、受飞行过程中各种扰动因素的影响较小、抗干扰能力强和落点精度高等优点,但是需要精度较高的火星大气模型和动力学模型。同时,在进入过程中每个制导周期都要重新规划飞行轨迹,并要求很高的计算速度,这对机载计算机的计算能力要求很高。
大气进入段的预测校正制导算法首次应用于美国的“双子座”计划中。“双子座”计划采用两种不同进入段预测校正制导策略[8]。第一种通过经典预测校正算法来预测落点误差并调整飞行轨迹;第二种则是采用全升力弹道式轨迹来预测终端纵程误差,通过不断翻转探测器来调整飞行轨迹。后来,Kluever等(2008)[9]采用一种在线预测校正制导算法,该算法假设一个常值的滚转角剖面以及安排了滚转角反转时间表,并通过给出的滚转角控制信号来实现飞行轨迹的控制。
3 进入段预测校正算法的步骤及其改进
本文介绍的火星探测进入段预测校正算法是在Brunner C W和Lu P(2008)[10]为月球返回任务提出的跳跃式进入段制导算法的基础上改进的。该预测校正算法的主要优点是它总是能确保探测器在一条能满足各种约束条件的轨迹上飞行,并且能获得适合的指令滚转角输出来控制飞船飞行。然而,该算法需要大量的计算时间,这个缺点削弱了上述的优点。该算法所需的总代码数远远多于其他的制导算法。因此本文提出了一种改进的预测校正算法来缩短在线计算时间。
3.1 纵程、横程和航程
在预测校正算法中,探测器的飞行航程被分解为纵向航程(纵程)和横向航程(横程),其定义分别如图1所示。
P1点为探测器的进入点,P2为期望的开伞点位置,P3为实际落点,过P1和P2点做经过地心的大圆弧,过P3点做一条与垂直的直线P3P4,称为探测器运行的纵程,P3P4为横程。而弧称为探测器实际运行航程,可以由如下方程

通过积分得到。

图1 航程示意图Fig.1 Illustration of crossrange and downrange during the entry
3.2 纵向预测校正算法
预测校正算法的核心是纵向平面制导算法,其大体上可以分为预测和校正2个环节,其中预测环节是根据当前初始状态和设计的滚转角策略数值积分得到终点的位置信息,然后校正环节根据位置信息与期望的位置进行比较,给出校正预测角。本文预测环节算法与文献[10]中的算法有不同之处,文献[10]中的预测滚转角选择为一种线性滚转角策略,即首先通过设置初始时刻和末端时刻的滚转角,然后其余各个时刻按照线性规律确定相应的滚转角,这种算法的设计较为复杂、计算量大。本文在预测环节采用一种较为简单的常值滚转角策略,其中每一个预测部分滚转角的选取如下文所述。
3.2.1 预测调整算法
预测环节的主要任务是计算需要完成的待飞航程Stogo和预测的航程Sp。其中待飞航程[11]Stogo可以表示为
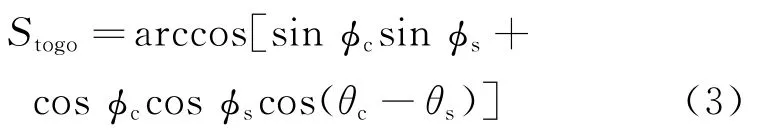
其中:下标C表示当前的位置;S表示目标点位置;θc,θs和ϕc,ϕs分别表示当前位置和目标点位置的经度和纬度。由此可以看出,待飞航程由当前位置的经度、纬度和目标开伞点的经纬度来决定的。对方程式(2)从当前时刻到开伞时刻进行积分便可以得到预测航程Sp。应当注意的是,上述的待飞航程和预测航程的单位均为弧度(rad)。
由于每个制导周期中都需要控制输入滚转角对动力学方程进行积分以得到预测航程,所以在预测环节中需要一个滚转角规划策略,称之为滚转角策略。本文采用一种最简单的滚转角策略—常值滚转角,该策略将当前的指令滚转角用到预测范围的每个制导周期中。对于常值滚转角策略而言,由于每一个制导周期内滚转角是恒定的,因此对于滚转角初始值的选取就显得尤为重要了。考虑到在进入段的初始时刻数值较小的滚转角能满足热负载、减速负载的限制要求,该算法在轨迹的数值仿真中假设给出的是10°的初始滚转角[10]。在进入段的中后期,一个较大的滚转角能够用来快速的降低速度以使得探测器能够满足飞行中的动压约束,此时在每个制导周期内滚转角要选取的大一些。然后在每一个预测周期按照已设定的滚转角规划策略得到探测器总的预测航程Sp,并与探测器需要完成的待飞航程Stogo作比较,最后求出待飞航程与预测航程之间的差值Δs。
需要指出的是,预测部分得到的滚转角并不是实际飞行时的滚转角,实际飞行时刻所采用的滚转角应当由预测和校正部分共同确定。
3.2.2 校正环节
校正环节的目的是当纵程的误差没有满足要求时,滚转角会被修正以使得所求的纵程误差足够小。根据经验可以得知预测的航程与当前的指令滚转角数值呈反相关。由航程差可知,为了增大预测的航程,指令滚转角数值应该减小。
本文应用一种迭代计算过程来进行滚转角的校正[11],迭代算法如下
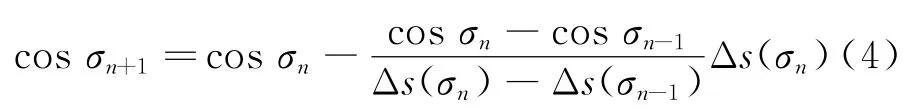
可以看出校正环节需要预测两次的航程差以得到新的滚转角。第一个采样周期来初始化这个迭代过程,首先需要一个初始的估计滚转角;另一个需要考虑的参数是在每个制导周期中第二次预测所需的滚转角增量。因为校正环节需要之前的两次预测来获得新的滚转角,所以在每个制导周期中第二次预测所需的滚转角需要通过增加第一次所预测滚转角的数值来得到。从仿真结果中可以看到,这个增量最好选取为30°~50°,可以显著地减少迭代的次数。
3.3 横向控制逻辑
为了使飞船能够朝着目标点飞行,还需要采用横向控制逻辑,通过滚转角翻转来将横向误差限制在一个可以接受的区域之内。对于具有低升阻比的火星探测器而言,本文采取的横向控制方法——横向误差的滚转角翻转策略,设计思路是:当探测器的横向航程超过所设定的阈值时,探测器滚转角的符号会翻转。其中横向航程的误差阈值可以为一个关于速度标量的二次型或简单的线性方程。根据计算,可以得到横向航程误差与探测器的待飞航程Stogo、探测所处位置的航向角以及在该处计算得到的天顶角Ψ有关[12]。
如果航向角误差超出了提前设定的阈值,横向控制逻辑就会翻转滚转角的符号。否则,滚转角的符号就会保持不变。这个方法的目的是使飞船朝着目标开伞点飞行。在最优的航程控制中,翻转的次数应该最少化,同时保持可以接受的横向航程误差控制。理论上来说,一次滚转角翻转就足以完成对横向误差的控制[13]。
3.4 航向制导
对火星精确着陆任务来说,在进入段探测器精确到达开伞点是必须条件。待探测器速度降到一定条件时,控制方式则由预测校正算法切换到航向制导控制算法,这样可以提高开伞点水平方向精度。本文在进入段的末端采用了一种航向调整的控制策略,这种控制策略的原理是根据经典的反馈线性化过程,确定关于航向角的一阶误差动力学方程,通过对期望航向角的设计使得探测器的航向角与输入的期望航向角相同,从而减少末端水平方向的误差。
用φd表示期望的航向角,φ为实际的航向角。其中期望的航向角可以进行人为的设定或者由飞行器的位置决定。定义航向角的误差如下式
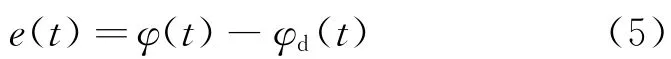
根据反馈线性化过程,我们确定了航向角期望的一阶误差动力学模型

若使得k1为正数,则误差会趋于零。将上式带入探测器的动力学方程(1)中,可以得到进入段末端的滚转角制导规律
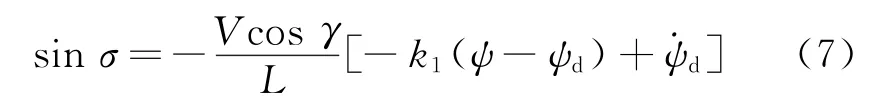
若调节参数k1选取得合适,探测器在进入段的末端会实现精确的制导,大大降低开伞点的水平误差。
4 改进的预测校正算法
尽管以上提出的预测校正算法能很好的实现精确制导的要求(见仿真结果),但是它至今还没有被运用在实际的制导过程中。其中一个主要的原因就是当前的机载计算机不能满足算法所需要的较快的计算速度。但是随着科技的发展,将来高速的计算机可能能够满足这一要求。另一种解决的方法就是我们通过改进现有的预测校正算法来减少所需的计算时间。
4.1 分段预测校正算法
基于以上所述,本文提出了一种改进的基于航路点的预测校正算法,并且采用一种分段制导的方法来提高精度,该分段制导法结合了预测校正和航向制导的优点,其过程如下:根据预测的进入点和目标开伞点位置预先设计好标称的轨迹;在标称轨迹上选取若干点作为航程点(目标点);使用上文详细介绍的预测校正算法来依次朝着每个目标点飞行;在进入段的末端采用航向制导法以提高探测器在开伞点的精度。
所选择的航程点可以作为换向的触发标志。当从上一个换相点到当前位置的航程等于这段轨迹两点间的待飞航程时,飞行器自动切换目标点,朝着下一个目标点飞去。这个基于航路点的预测校正算法不仅能保持传统预测校正算法的优点:对初始扰动不敏感,同时又能显著地减少总的计算时间。
4.2 过程约束与航程点的选择
火星探测器在进入段的飞行当中,由于受到火星大气不确定性、火星自转等因素的影响,使得探测器在进入段飞行时受到各种飞行过程约束的制约,其中最典型的过程约束包括:热流约束、过载约束以及动压约束。过程约束的方程式如下[14]
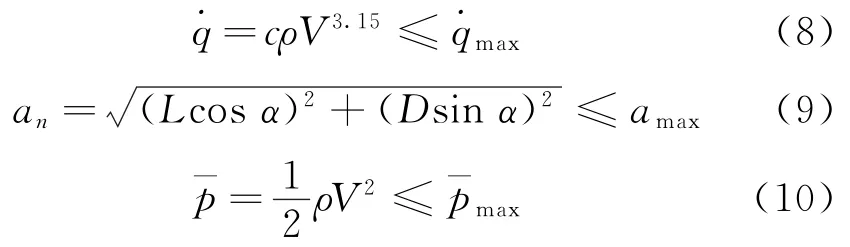
其中:c为热流常数项;ρ为火星大气密度;an为探测器飞行过程中所受到的过载加速度;α为探测器的飞行攻角;m为探测器的自身质量;为动压;分别表示探测器在飞行过程中所受到的热流、过载和动压的峰值。可以看出:若探测器能够安全飞行直至到达目标开伞点,则整个飞行过程就必须满足这3个过程约束。
对探测器进行动力学分析可以发现,在进入段的初始阶段由于探测器的飞行速度较大,因此主要考虑热流约束是否满足;当探测器的速度降为2000m/s左右时,此时探测器的升力和阻力会达到一个峰值,因此这段时间内动载是主要的考虑因素;在探测器的飞行末端,由于所设计的开伞点对于探测器的末端速度有着较高的要求,因此在探测器的末端动压约束就成为主要过程约束,可以看出航程点的选择就要根据过程约束来确定。此外,在最优的航程控制中,目标之一是在保持可以接受的横程误差条件下,滚转角的翻转次数应该最少。根据气动力学方程,当滚转角增大时,航向角偏差增大,因此在保证航程误差的条件下,应尽量减小滚转角以减少翻转次数。
5 仿真结果
本文采用“火星科学实验室号”的数据来进行数值仿真实验[15],飞行器进入段的初始以及末态位置、姿态信息如表1所示。

表1 进入段的初态和末态信息Table1 Theinitialandterminalconditionsofthevehicle duringtheentryphase
根据上表中关于进入段的信息参数对文章中的算法进行仿真,仿真结果如图2所示。
图2表示校正时采用固定的滚转角增加量所得到横程及其阈值,图3表示改进后采用分段预测校正算法所得到的横程及其阈值关系图。可以看出改进后,在保证横程误差不变的前提下,滚转角翻转的次数有所减少。
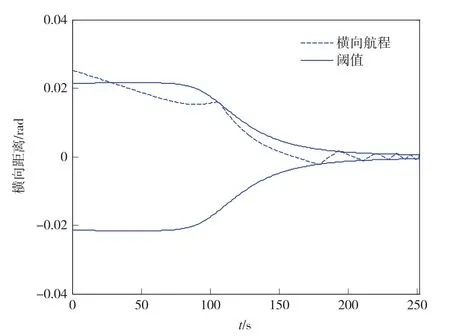
图2 预测校正算法得到的横程及其阈值Fig.2 Crossrangeandthresholdusingthepredictor-corrector algorithm
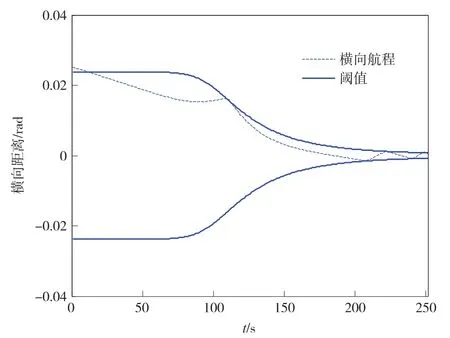
图3 分段预测校正算法得到的横程及其阈值Fig.3 Thecrossrangeandthresholdusingsegmentguidance predictor-correctoralgorithm

图4 预测校正算法生成的轨迹图Fig.4 Thetrajectoryusingpredictor-correctoralgorithm
图4和图5分别显示了执行预测校正算法和分段预测校正算法时的轨迹曲线图。为了简单起见,我们从预先设计的轨迹上选取了3个点。这3个点的坐标分别是(-84°,-43.24°),(-80°,-42.71°),(-76°,-42.07°)这三个坐标点的选取分别是按照满足动压约束最大值、加速度约束最大值和速度约束最大值来进行选取的。飞行器在每个阶段采用分段预测校正制导飞行,朝着目标点飞行。

图5 分段预测校正算法生成的轨迹图Fig.5 The trajectory using segment guidance predictor-corrector algorithm

图6 预测校正算法得到的开伞点位置分布图Fig.6 Deployment positions using predictor-corrector algorithm

图7 分段预测校正算法得到的开伞点位置分布图Fig.7 Deployment positions using segment guidance predictorcorrector algorithm
仿真是在Intel Core 2 Duo T6600,2.2 GHz CPU的电脑上进行的,制导周期设置为1 s。两种算法的计算时间分别为:3.601 s和1.824 s,由此可以看出,分段制导的仿真时间仅是传统预测校正算法仿真时间的一半。
预测校正制导算法和分段制导算法目标开伞点位置坐标的蒙特卡洛仿真结果如图6和图7所示。其中2个圆圈分别表示距离目标点5 km和10 km的距离。图6的结果显示采用预测校正算法时,进入段的降落点中大约有98%离目标点的距离在5 km之内,全部都在10 km的范围之内;采用分段制导算法的开伞点精度要低于采用传统预测校正算法的精度,有86%的末端降落点在离目标点5 km的范围内,但全部降落点都在10 km的范围内,这是因为分段制导在每个阶段都有一定的误差积累。两种制导算法的平均纵程误差基本相同,这就证明了分段制导能像传统的预测校正算法一样有效地将纵程误差控制在可接受的范围之内。
因此,仿真结果证实了传统的预测校正算法和改进的预测校正算法——分段制导算法在有很大不确定性的情况下具有很强的鲁棒性和可靠性,并且可以实现精确着陆的要求。尽管分段制导的横程误差比传统的预测校正算法大,但是该误差仍在一个可以接受的范围之内。与此同时,分段制导方法具有较少的仿真时间,这表明了它可以在实际制导应用中显著地减少飞船在线计算时间。
6 结 论
文章主要介绍了在较低的升阻比条件下,对火星着陆器的一种新型制导控制方法——预测校正算法进行了研究。这种制导策略包括一个纵向的预测校正制导、一个横向控制逻辑和飞行末段的航向制导策略。其中在纵向制导中,滚转角的数值能自动地改变来满足纵程误差的要求;当横向航程误差大于提前选定的阈值时,滚转角的符号会发生翻转。最后,航向调整控制器会使飞船朝着目标开伞点飞行。此外,仿真结果证实了该算法的鲁棒性和可靠性,以及其减少飞船在线计算时间的优点。
[1]Martin J L Turner.Expedition Mars:how we are going to get to Mars[M].Berlin:Springer,2004.
[2]Barlow N G.Mars:an introduction to its interior,surface and atmosphere[M].Cambridge,UK:Cambridge University Press,2008.
[3]胡中为,徐伟彪.行星科学[M].北京:科学出版社,2008:40 60.[Hu Z W,Xu W B.Planetary science[M].Beijing:Science Press,2008:40-60.]
[4]Andrew B,James G,Ralph.Planetary landers and entry probes[M].Cambridge,UK:Cambridge University Press,2010.
[5]周美江.火星EDL轨迹优化和进入制导研究[D].哈尔滨:哈尔滨工业大学,2012.[Zhou M J.Trajectory optimization for Mars EDL and research on the entry guidance[D].Harbin:Harbin Institute of Technology,2012.]
[6]Manrique J B.Advance in spacecraft atmospheric entry guidance[D].Irvine:University of California,2010.
[7]Xia Y Q,Chen R F,Pu F,et al.Active disturbance rejection control for drag tracking in mars entry guidance[J].Advances in Space Research,2014,53(5):853-861.
[8]Mease K D,Kremer J P.Shuttle entry guidance revisited using nonlinear geometric method[J].Journal of Guidance,Control and Dynamics,1994,17(6):1350-1356.
[9]Kluever C A.Entry guidance performance for Mars precision landing[J].Journal of Guidance,Control,and Dynamics,2008,31(6):1537-1544.
[10]Brunner C W,Lu P.Skip entry trajectory planning and guidance[J].Journal of Guidance,Control,and Dynamics,2008,31(5):1210-1219.
[11]Powell R W.Numerical roll reversal,predictor-corrector aero capture and precision landing guidance algorithm for Mars Surveyor program 2001 missions[C]∥AIAA Atmospheric Flight Mechanics Conference.[S.l.]:AIAA,1998.
[12]Carman G L,Ives D G,Geller D K.Apollo-derived Mars precision lander guidance[C]∥AIAA Atmospheric Flight Mechanics Conference.Boston.MA,USA:AIAA,1998.
[13]Mease K D,Leavitt J A,Benito J,et al.Advanced hypersonic entry guidance for Mars pinpoint landing[C]∥Proceedings of the NASA science technology conference.MD,USA:AIAA,2007.
[14]Xue S B,Lu P.Constrained predictor-corrector entry guidance[J].Journal of Guidance,Control,and Dynamics,2015,33(4):1273-1281.
[15]Shen G H,Xia Y Q,Sun H R.A 6 DOF mathematical model of parachute in Mars EDL[J].Advances in Space Research,2015,55(7):1823-1831.
通信地址:北京市海淀区中关村南大街5号,北京理工大学自动化学院(100081)
E-mail:xia_yuanqing@bit.edu.cn
沈刚辉(1991—),男,硕士研究生,主要研究方向:火星探测进入段制导控制。
通信地址:北京市海淀区中关村南大街5号,北京理工大学自动化学院(100081)
E-mail:hxyzsgh@gmail.com
Mars Entry Guidance Based on Predicted Corrector Algorithm
XIA Yuanqing,SHEN Ganghui,SUN Haoran,ZHOU Liuyu
(School of Automation,Beijing Institute of Technology,Beijing 100081,China)
This paper describes the development and evaluation of the common numerical predicted corrector algorithm and gives an improved algorithm for the Mars entry guidance.First,it introduces two guidance strategies:tracking the reference trajectory and predicted corrector algorithm,finding that the common predicted corrector algorithm can be less sensitive to initial dispersions,but needs fast on-board computation;Second,the downrange algorithm,lateral control logic and heading alignment are described in details,which are provided to improve the horizontal accuracy of the vehicles;Furthermore,the segmented guidance predicted corrector algorithm is used to shorten the on-board computational time.Simulation results show that this entry guidance algorithm demonstrates reliable and robust performance in situations with high uncertainties.
entry guidance method;predictor-corrector;lateral control;heading alignment
V9
A
2095-7777(2015)04-0338-07
10.15982/j.issn.2095-7777.2015.04.007
夏元清(1971—),男,教授,博士生导师,主要研究方向:多源信息复杂系统的信息处理与控制;飞行器控制;空天地一体化网络协同控制等。
[责任编辑:高莎]
2015-08-01
2015-10-20
国家重点基础研究发展计划(973计划)(2012CB720000);国家自然科学基金资助项目(61225015);国家自然科学基金创新群体项目(61321002)

