一种基于星载GPS的月球探测器导航算法
刘也,曹建峰
(1.航天飞行动力学技术重点实验室,北京100094;2.北京航天飞行控制中心,北京100094)
一种基于星载GPS的月球探测器导航算法
刘也1,2,曹建峰1,2
(1.航天飞行动力学技术重点实验室,北京100094;2.北京航天飞行控制中心,北京100094)
为验证GNSS旁瓣信号对中高轨航天器在轨飞行的导航支持能力,“嫦娥5号”飞行试验器搭载了GPS导航接收机。由于目前使用的星载导航解平稳性不够,为此,根据月球探测器不同飞行段落轨道动力学特性,建立了一种基于星载GPS数据的月球探测器实时导航算法。该算法充分考虑了月球探测器不同段落的动力学特性,基于UKF滤波设计,并引入了自适应策略,以降低滤波参数选取的难度。在分析星载GPS数据特点基础上,月地返回段实测数据的处理结果验证了算法的可行性和有效性。
卫星导航;自适应滤波;“嫦娥5号”飞行试验器
0 引 言
2014年10月24日,“嫦娥5号”(Chang’e-5 test vehicle,CE-5T)飞行试验器发射,历时9 d的飞行,验证了再入返回技术。飞行器上首次搭载了GPS导航接收机,用于验证GNSS旁瓣信号对中高轨航天器在轨飞行的导航能力。这是一次全新的尝试,以往“嫦娥1号”和“嫦娥2号”任务,地月转移和环月飞行阶段主要是利用地基USB/UXB(unified S/X-band)与VLBI(very long baseline interferometry)测量数据,获取100 m量级的轨道通常需要近10 h的测轨数据支持[1],而当面临频繁的姿轨控时却难以满足。实际上,早在20世纪90年代,就有人提出了将GNSS旁瓣信号用于中高轨航天器导航的设想[2]。德国于1997年发射了Equatorial-S卫星,高轨航天器GPS搭载试验首次获得成功[3]。美国哥达德航天中心也尝试开发高轨航天器的GPS接收机并进行了试验[4]。此外,美国国家航天局还研发了适用于月球探测器的GPS接收机,但未进行搭载试验[5]。然而,国内关于GNSS在高轨及月球探测器的相关研究起步较晚,并且主要集中于GPS信号覆盖特性和观测能力等方面的研究,星载GNSS导航算法相对简单,存在一些数据跳点,且平稳性较差,高精度的定轨结果还主要依赖于事后长弧段的定轨分析[67]。
为了验证“嫦娥5号”搭载GNSS数据的实时导航性能,本文在充分考虑月球探测器不同段落的动力学特性基础上,提出一种基于自适应UKF(unscented kalman filter)滤波的月球探测器实时导航算法,并利用“嫦娥5号”地月返回段数据进行了计算分析。
1 基于星载GPS的月球探测器导航算法
1.1 导航模型
航天器导航解算是基于准确的导航模型,包括测量模型与运动模型。对于星载GPS系统,测量数据包括伪距测量和星载导航求解两类。记航天器真实位置X=[x y z]T伪距测量公式如下
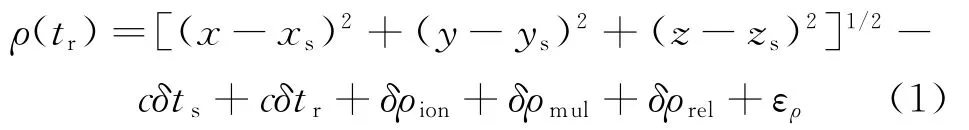
其中:下标s、t、r、ion、mul、rel分别代表卫星钟差、接收机钟差、电离层延迟、多路经效应、相对论效应;Xs=[xs,ys,zs]T为导航星位置。此外,星载接收机具有滤波功能,因此下传的导航解非纯单点定位。在滤波收敛不稳定的条件下,直接下传单点定位解,否则下传滤波结果,本文中统称为导航解。记导航解测量结果,导航解的测量方程为
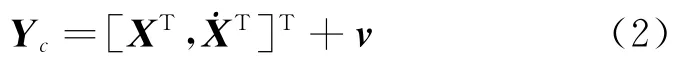
实际上,原导航解作为测量输入时,不妨将其看作是一个预处理过的测量数据,这样算法改进了导航性能,并且有移植到星上处理的潜力。
航天器运动模型可统一描述为
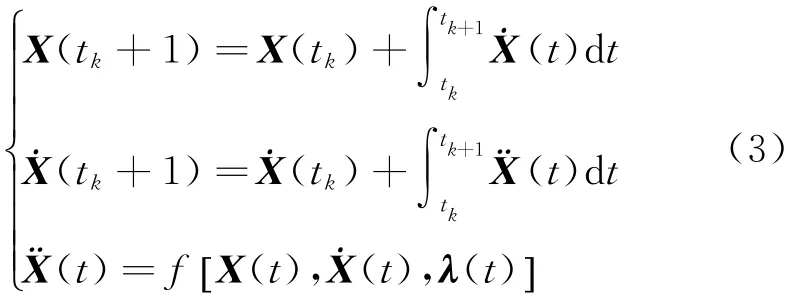
其中:λ(t)为加速度的模型参数(包括物理参数和新引入的参数),由于加速度随着位置和速度变化,为得到离散化的状态方程,式(3)的积分可以采用数值积分方法计算。对于月球探测器,上述模型建立的关键是通过其动力学特性分析,获得加速度计算公式。
月球探测器飞行过程主要是处于日、地、月引力系统内,此外还受太阳光压、地球大气等的影响。对于实时导航系统,从计算效率和精度的折中考虑,摄动力较小可以忽略,此时的飞行过程如图1所示,实时导航时可以大致分为近地段(发射段、绕地段及再入返回段)、地月转移段和环月段。通过摄动力量级分析以及大量的仿真计算结果,确定了如表1所示的轨道计算策略。导航系统中只解算航天器位置与速度,力模型中的相关参数(如航天器面质比等)都采用事前装订的模式,模型不符合部分则吸收到滤波器参数中,由此就确立了航天器不同飞行阶段的定轨模型。其中每种力模型的计算公式可以参考相关文献,这里不再赘述。需要注意的是,这里的环月段为了计算简便,采用月球质心为坐标原点。由于各段落间并没有明显的界限,为保证导航结果的平滑型,滤波器切换时需要一定的自适应策略,详见本节第3部分。
1.2 实时滤波算法
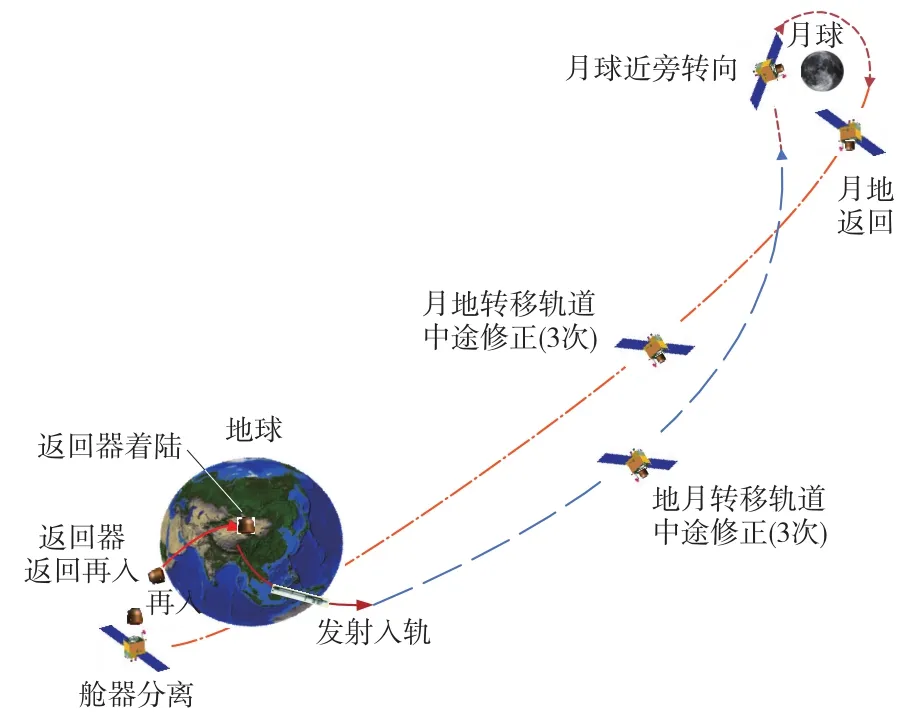
图1 再入返回试验中的月球探测器轨道Fig.1 Orbit of lunar detector in the reentry test

表1 月球探测器不同飞行段落导航时的轨道计算策略Table 1 Orbit calculation scheme for lunar detector in different flying phase
1.1 节建立的导航模型是一个典型的非线性系统状态估计问题,目前的实时算法普遍基于各种非线性滤波方法实现,常用的如扩展Kalman滤波(extended kalman filter,EKF)、无迹滤波(the unscentedkalman filter,UKF)和粒子滤波(particle filter,PF)等。鉴于计算实时性和跟踪精度的需求,下面采用UKF[8]推导导航系统的实时滤波算法。
设已获得k-1时刻目标轨道估值Xk-1|k-1及其误差协方差矩阵PX,k-1,对其采样得到Sigma点及其权矩阵,i=1,2,…,L,L为采样点总数,采样方法可参考相关文献[8]。滤波过程如下:
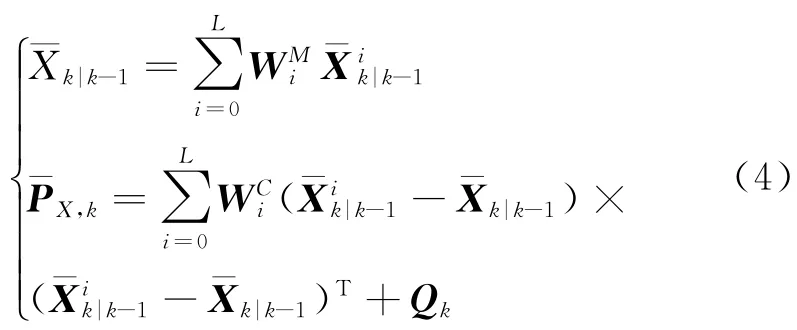
为状态预测均值和协方差矩阵;Qk为状态噪声。
2)测量预测

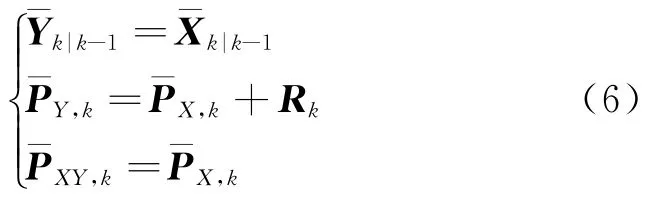
3)状态滤波为

2 滤波器自适应
滤波算法的输出是模型预测状态和实际观测状态的加权融合,由于所用运动模型并不能精确刻画目标运动状态,而测量过程也不可避免地出现各种测量误差,融合权值应该由测量精度和模型预测精度共同确定。一般通过输入滤波器的状态噪声和测量噪声方差来反映这种不确定性(精度),它们可先验给定,但通常很难获得对所有运动和测量情况普适的方差参数,因此这里引入噪声开窗统计策略。此外,由于导航系统根据月球探测器设定了三个解算段落,还需要给定不同解算段的自适应策略。
2.1 噪声自适应
设tk时刻统计窗内含l个采样点,记状态误差)的协方差;状态预测和估计误差协方差矩阵为和PX,k;状态噪声协方差为Qk;状态误差预测函数为f(·);根据Kalman滤波实现过程

引入衰减记忆因子αx(αx∈[0,1]),则

类似的,记tk时刻测量预测误差协方差矩阵,测量噪声矩阵Rk,窗口内测量误差的协方差ΣΔY,可得测量噪声协方差的自适应估计

其中:αY为衰减因子;的计算与式(8)类似。
2.2 运动模型自适应
表1给出了航天器不同飞行段落所用的运动模型,但实际工程中各段落间并没有明显的时间分割点。为了保证导航结果的平滑,在各段落交界范围内,我们设置一定的模型自适应区间。该区间内,滤波器采用交互多模的方式,备选模型有两类,即该区间两端飞行段落所对应的运动模型。模型交互方法可参考相关文献[9],这里不再赘述。稍有不同的是,为了实现飞行段落过渡,在每步滤波过程中,会将区间右侧模型的转移概率适当放大。设tk时刻转移概率矩阵为Pk=[p11,p12;p21,p22],0<α<1,则

3 “嫦娥5号”计算实例
“嫦娥5号”试验期间,星载GPS接收机共开机2次,分别是地月转移段的初期与月地返回段的末期,2次试验均成功获取了导航解(地固坐标系位置速度)以及伪距测量数据。本文采用的算法——自适应UKF算法对测量数据有一定的普适性。伪距和相位的数据预处理工作更加复杂,故没有作为算例给出。因此,这里主要利用GPS导航解数据进行计算分析,数据采样率1 Hz。本次任务环月段未安排GPS测量,故实际数据的处理工作还需在以后的研究中验证。以事后精密轨道确定结果为基准,初始状态噪声方差影响不大,这里选择对角线为10-8的单位矩阵,滤波噪声自适应参数的选取与实际问题有关,在月球探测器的仿真和实际处理中,通常选取(0.01,0.1],具体取值影响并不显著,这里选择为0.05。
两个段落的导航解误差如图2和图3所示,两段误差曲线均存在一些跳点和发散的现象。特别在离地球较远的段落,可视导航卫星数量少、信号弱,滤波器存在异常。即使滤波收敛后,其速度误差曲线仍然有很大的抖动,导航解平稳性有待加强。这是由于星载导航滤波结果是由滤波和单点定位组合而成,在滤波收敛不稳定的条件下,直接下传单点定位解,否则下传滤波结果。而滤波器所用运动模型相对简单,且自适应调节能力较差,需要一定的测量数据使得滤波趋于稳定,因此观测几何不好或动力学模型不准确时,可能会导致滤波收敛异常。
应用本文提出的自适应滤波算法,对GPS数据进行导航解算,结果表明,算法可以在20个采样点左右实现收敛,收敛后数据中断跳点现象可以被剔除,数据缺失的段落则能通过滤波器预测机制实现了平稳过渡。其中,月地返回段滤波结果如图4所示,可见本文方法能够自适应导航数据质量的变化,且误差曲线抖动较原始星载导航结果明显减小,表明导航结果的平稳性得到明显改善。由图4也发现,自适应方法引入之前,滤波结果因模型约束力较强,存在解算滞后现象,表现为误差峰值的后延,特别是左图的位置滤波结果尤其明显。此外,滤波器收敛后,估计结果与事后高精度轨道相差在百米以内,可以认为这里的导航算法达到了百米左右的估计精度。

图2 地月转移段星载GPS导航解误差Fig.2 Navigation error of the satellite-borne GPS for lunar transfer orbit
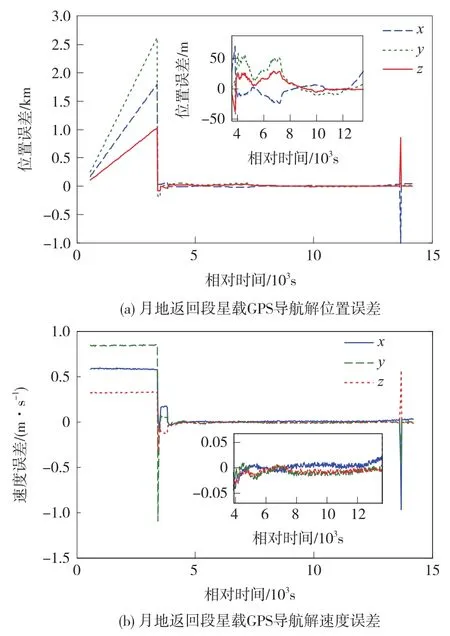
图3 月地返回段星载GPS导航解误差Fig.3 Navigation error of the satellite-borne GPS for circumlunar return orbit

图4 不同算法在月地返回段的导航误差Fig.4 Navigation errors of different algorithms for circumlunar return orbit
4 结束语
本文设计了一种自适应UKF滤波算法,可用于月球探测器实时导航算法。基于“嫦娥5号”搭载了GPS接收机的测量数据,获得了比现有导航解更加平稳的轨道实时估计结果,且精度也有一定的改善。受试验数据来源限制,本文的算法验证主要基于月球探测器地月转移段。后续将在仿真计算的基础上,寻找合适数据源,对其它飞行阶段以及各阶段的切换段落进行验证,为建立适应航天器全寿命的自适应的导航滤波器提供技术参考。
[1]陈明,张宇,曹建峰,等.嫦娥二号卫星轨道确定与测轨技术[J].科学通报,2012,57(9):689-696.[Chen M,Zhang Y,Cao J F,et al.Orbit determination and tracking technology of CE-2 satellite[J].Chinese Science Bulletin,2012,57(9):689-696.]
[2]Lichten S M,Estefan J A.High-precision orbit determination for high-earth elliptical orbiters using the global positioning system,AIAA-90-2954-cp[R].USA:AIAA.1990:664-673.
[3]Lemke N,Eissfeller B,Enderle W,et al.Tracking GPS above GPS satellite altitude:first results of the GPS experiment on the HEO mission Equator-S[C]∥Position Location and Navigation Symposium.Munich:IEEE,1998:243-249.
[4]Winternitz L,Bamford W A,Hechler G W.A GPS receiver for high-altitude satellite navigation[J].Journal of Selected Topics in Signal Processing,2009,3(4):541-556.
[5]Bampford W A,Hechler G W,Holt G N,et al.A GPS receiver for lunar missions[C]∥Proceedings of the 2008 National Technical Meeting of the ION.San Diego CA:[s.n],2008:268-278,
[6]刘海颖,王惠南.基于GPS的中、高轨道航天器定轨研究[J].空间科学学报,2005,25(4):293 297.[Liu H Y,Wang H N.Orbit determination of satellite on the middle-high earth orbit based on GPS[J].Chinese Joural of Space Science,2005,25(4):293-297.]
[7]Yang Y,Li J,Xu J,et al.Contribution of the compass satellite navigation system to global PNT users[J].Chinese Science Bulletin,2011,56(26):2813-2819.
[8]Julier S J,Uhlmann J K.A new extension of the Kalman filter to nonlinear systems[C]∥International Society for Optics and Photonics.Orlando:[s.n],1997:182-193.
[9]Li X R,Jilkov V P.A survey of maneuvering target tracking—Part V:multiple-model methods[J].IEEE Transactions on Aerospace and Electronic Systems,2003(11):1-57.
通信地址:北京市5130信箱120分箱(100094)
电话:(010)66362455
E-mail:liuye_new@sina.com
Navigation Algorithm for Lunar Probe Based on Satellite-Borne GPS Data
LIU Ye1,CAO Jianfeng1,2
(1.National Key Laboratory of Science and Technology on Aerospace Flight Dynamic,Beijing 100094,China;2.Beijing Aerospace Control Center,Beijing 100094,China)
To validate the navigation ability for high orbit spacecraft by side-lobe echo of GNSS,GPS receiver was fitted to the Chang’e-5 test vehicle.However,the system has not obtained an anticipant stationary position results.Therefore,a real-time navigation algorithm for lunar probe by satellite-borne GPS is suggested.The algorithm is developed by several UKF filter design according to different dynamic characters of the reentry test orbit.Adaptive technique is also introduced for filter switching and parameter selection.After the analysis of satellite-borne GPS,actual data from the circumlunar return of Chang’e-5 test vehicle is utilized for validating the feasibility and effectiveness of the algorithm.
satellite navigation;adaptive filter;Chang’e-5 test vehicle
V557.1
A
2095-7777(2015)04-0313-05
10.15982/j.issn.2095-7777.2015.04.003
刘也(1982—),男,博士,主要研究方向:航天器实时跟踪、数据处理及信息融合等。
[责任编辑:杨晓燕]
2015-09-21
2015-10-18

