地月平动点中继应用轨道维持

刘磊,曹建峰,胡松杰,唐歌实

(1.航天飞行动力学技术重点实验室,北京100094;2.北京航天飞行控制中心,北京100094)

地月平动点中继应用轨道维持

刘磊1,2,曹建峰1,2,胡松杰1,2,唐歌实1,2

(1.航天飞行动力学技术重点实验室,北京100094;2.北京航天飞行控制中心,北京100094)

地月平动点中继应用轨道对于月球背面探测具有十分重要的应用价值,由于地月平动点的不稳定性,必须进行轨道维持。文章研究了真实力模型下月球平动点中继应用轨道的维持。首先,基于限制性三体问题下平动点轨道的运动特性,研究了平动点轨道维持的数学模型与维持策略,提出了平动点轨道维持的连续环绕控制方法,并给出了轨道维持的Halo和Lissajous两种控制方式;其次,充分考虑各天体和光压摄动下,采用数值手段研究了不同幅值的地月平动点周期中继应用轨道的维持间隔与速度增量等。研究结果表明:Lissajous控制方式适用于月球平动点中继应用轨道的维持,在给定测控精度条件下,维持间隔约7.4 d,速度增量优于20 m/s/a。该方法已经成功应用于我国“嫦娥2号”日地平动点任务和“嫦娥5T1”地月平动点任务并获得了良好的控制效果,还可直接应用于我国未来“嫦娥4号”等月球背面探测任务。

平动点;轨道维持;限制性三体问题;Halo轨道;Lissajous轨道

0 引 言

当前,我国的深空探测活动主要集中在月球,“嫦娥1号”到“嫦娥3号”月球探测器已经圆满完成了任务,尤其是“嫦娥2号”在实现既定工程和科学目标的基础上,开展了日地平动点拓展任务和小行星飞越探测任务,取得了我国首次日地平动点飞行和世界上首次获取4179小行星近距离光学图像等多项突破性成果[1-4]。2014年下半年又开展了为后续“嫦娥5号”任务验证相关技术的“嫦娥5T1”再入返回飞行试验,之后进行了地月平动点探测飞行拓展任务[5]。虽然目前我国探月工程的着月点选择相对在地球始终可见的月球正面,但是人类探测较少的月球背面和两极地区,可能蕴含丰富资源,具有更高的探测价值,我国后续“嫦娥4号”将开展月球背面探测。受地月相对运动特性影响,在未来探测月球两极和背面区域时,必须考虑中继测控手段。

地月平动点相对于地球和月球位置始终固定,尤其是其中的L2点对于月球背面始终可见且距离月球较近,从而可以考虑设计月球L2点中继应用轨道,进行长期轨道维持使之始终保持与地球和月球背面的可见性,为月球探测器的留轨舱和着陆器提供中继通信和导航等服务。虽然当前平动点轨道动力学与控制等研究较为充分[610],不过平动点的应用目前仍集中于日地平动点,相对于日地平动点,地月平动点动力学特性较为复杂,其中太阳引力和光压对于轨道的摄动影响较大,且月球相对于地球运动具有一定偏心率,这些因素使得地月平动点轨道的稳定性较差,基于圆型限制性三体问题设计的周期轨道在真实力模型下很快发散,不再呈现周期运动特性。

为此,本文面向月球平动点中继应用,研究真实力模型下中继应用轨道的维持,给出相应的平动点轨道维持方法和策略,分析平动点中继应用轨道的维持频率和速度增量,确定不同幅值轨道的维持代价,为我国后续“嫦娥4号”和未来月球背面探测等任务提供借鉴。

1 轨道维持

1.1 数学模型

平动点属于限制性三体问题,即研究小天体在两大天体引力作用下的运动,设小天体的质量为m,其余两个大天体的质量分别为m1和m2,有m≪m2＜m1。首先单位归一化,大天体质量之和、大天体相互运动椭圆半长轴和角频率为1,以两大天体的共同质心为原点O,二者相对运动平面为xy平面,建立会合坐标系O-xyz,如图1所示。在研究平动点附近的运动时常将原点移至平动点处,即图1中的L1或L2。

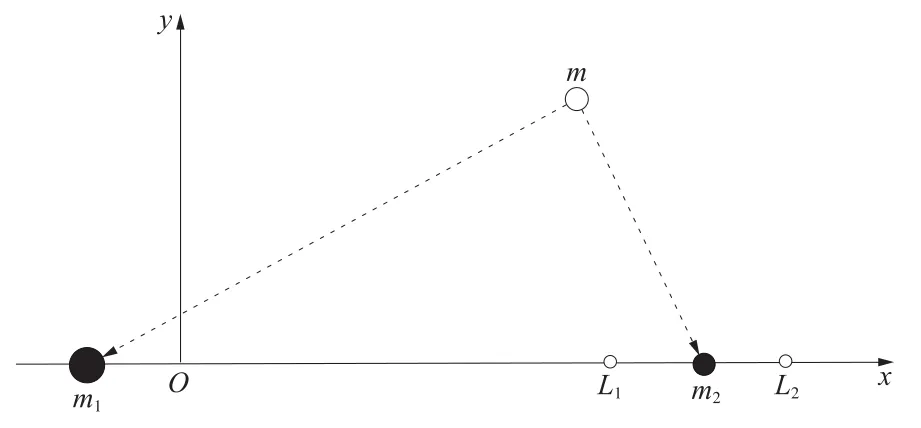
图1 会合坐标系Fig.1 Synodic coordinate

由小天体的动力学方程可得到O-xyz中共线平动点附近运动的一阶形式[9]

其中:Ax和Az分别为x和z方向的运动幅值;η和ζ分别为x和z方向的运动频率,一般为Lissajous轨道,在二者相等时即Halo轨道;φ和ψ分别为x和z方向的初始相位。

由式(1)可见,在一阶解析形式下,Halo轨道关于会合坐标系xz平面对称,且在xz平面附近运动方向垂直于xz平面,Lissajous轨道则在穿过xz平面时x方向速度为0,基于平动点轨道的运动特性,选择平动点轨道的理想末状态xd位于xz平面。由初始状态x0积分至Δy时刻的末状态一般与xd不相同,通过修正x0和t使得实际末状态接近xd。设x0和t的修正量分别为δx0和δt,则在一阶近似下有

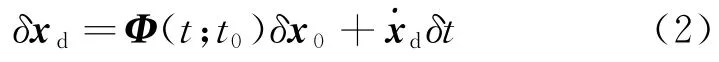
其中:Φ(t,t0)为转移轨道从初始t0时刻到t时刻的状态转移矩阵,即

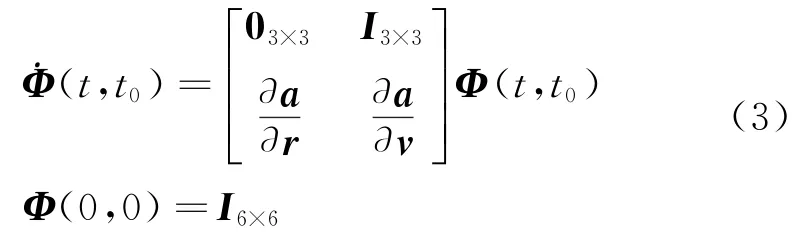
其中:r、v和a分别为卫星的位置矢量、速度矢量和加速度矢量,其中a的计算中考虑各种摄动因素即可反应该因素对转移轨道的影响。不过,在考虑摄动因素较多的情况下Φ(t,t0)的计算量较大,对于地月平动点轨道,因此仅考虑日地月质点引力和光压摄动即可满足计算精度和速度要求。

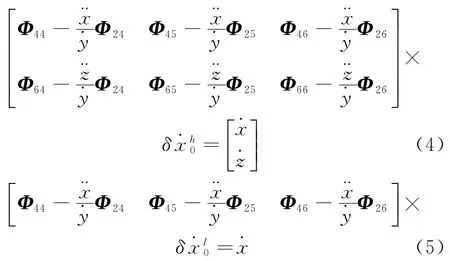
其中:Φij(i=2,4,6;j=1,3,5)表示Φ(t;t0)的第i行第j列个分量。

式(4)和式(5)即平动点轨道的连续环绕控制方法的两种形式,分别称为Halo控制方式和Lissajous控制方式,对于平动点周期轨道,两种形式均可采用,平动点拟周期轨道则采用后者。同时,式(4)和式(5)为基于平动点轨道一阶近似解的结果,因此需要采用微分修正方式进行多次迭代才可以获得理想的轨道末状态。

1.2 维持策略

1.1 小节的平动点轨道连续环绕控制方法,利用圆型限制性三体问题下平动点轨道的运动特性进行轨道维持,使得轨道末状态的x和(或)z方向速度为0。然而考虑到实际摄动力作用,轨道末状态的x和(或)z方向虽然接近0,但是并不严格为0,因此直接由式(4)和式(5)得到的维持速度增量将大于实际所需速度增量,且控后轨道偏离最优维持轨道,所以需制定相应的轨道维持策略。

为了利用式(4)和式(5)实现真实力模型下的平动点轨道维持,制定平动点轨道连续环绕控制策略,如图2所示。

图2中,LP为平动点,○和*分别表示轨道初始点和末端。首先定义平动点轨道由会合坐标系xz平面出发,再次到达xz平面为1/2圈,第3次到达xz平面则为1圈。轨道维持时,基于2.1小节的轨道维持模型式(4)和式(5),采用微分修正法改变轨道初始状态,使得积分1/2圈时x和(或)z方向速度为0,由此得到第1步修正后的轨道Corr1。虽然Corr1并非能量最省的平动点轨道,但是该轨道可以保持在平动点附近不会飞离平动点。然后再次修正初始状态,使得积分1圈时x和(或)z方向速度为0,得到修正后的轨道Corr2,该轨道进一步接近能量最优轨道。如此进一步延续下去得到修正后的轨道Corr3……,该策略即平动点轨道连续环绕控制策略。

图2 平动点轨道连续环绕控制策略Fig.2 Continue-circling method of the relay orbit maintenance

由此可见,上述连续环绕控制策略利用圆型限制性三体问题下平动点轨道的运动特性,通过逐步延长轨道弧段并渐进修正初始轨道状态,最终获得真实力模型下维持能量近似最优的平动点轨道。该策略有两处需要特别说明,其一,虽然图1中每步维持以1/2圈轨道增加,但是实际计算时可根据迭代收敛容限和具体三体系统进行调整,在收敛容限和轨道摄动较小情况下,平动点轨道维持间隔可适当放大;其二,理论上延续步骤越多,轨道维持的能量越接近最优。不过实际计算表明,在延续2圈以后,轨道的修正量已经极其微小,因此最大延续轨道弧段不应超过2圈,地月系平动点轨道则最大取1.5圈即可。

2 数值仿真

设计Az为5 000 km和30 000 km的地月L2点周期轨道作为月球平动点中继应用轨道,分别采用Halo和Lissajous控制方式进行长期维持,研究2种方式的有效性。仿真中考虑光压和大行星引力摄动,光压系数取1.3,行星位置采用JPLDE405星历。同时,为了分析2种方式的轨道维持能力,仿真中基于国内外目前的测控能力,设定两组大小不同的测控误差,较大的测控误差为位置精度5 km,速度精度为1 cm/s,控制精度为2%,同时考虑5 cm/s的剩余控制误差,较小的测控误差为位置精度1 km,速度精度为1 cm/s,控制精度为1%,无剩余控制误差。

2.1 Halo控制方式

在较大测控误差下,仿真Az为5 000 km的中继应用轨道维持,总时间为2年。采用蒙特卡洛打靶法分析,共进行200次仿真,各次仿真所需要的总速度增量Φ(t1;t0)和轨道周期(两次穿越xz平面的时间间隔)i变化如图3所示,上图横坐标n为仿真次数,下图横坐标nk为轨道维持圈次。由于误差和摄动影响,轨道维持间隔为1/2个轨道周期,延续控制最大时长为3/2圈,即使得第3次穿越xz平面时x和z方向速度小于1 m/s。

图3 较大测控误差下小幅值Halo轨道维持2年的情况(Halo方式)Fig.3 Orbit maintenance of the small Halo orbit for 2 years with the large TT&C errors(Halo style)

由图3可见,2年维持时间内,维持的总速度增量除极个别情况超过300 m/s,绝大多数不超过200 m/s,平均为155 m/s左右。轨道周期呈现周期变化,约为14～16 d。

给出仿真中总速度增量超过300 m/s的中继轨道在2年内的空间变化图,及其在会合坐标系各坐标平面的投影图,如图4所示。

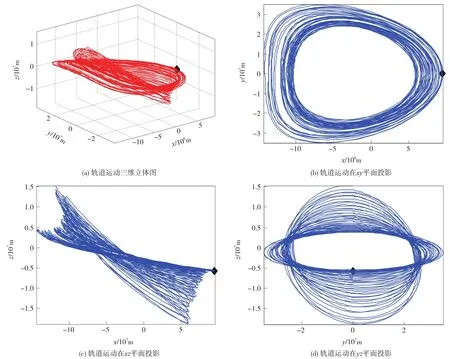
图4 较大测控误差下小幅值Halo轨道维持总速度增量最大的情况(Halo方式)Fig.4 Case with the maximum velocity increment of the small Halo orbit with the large TT&C errors(Halo style)

由图4可见,总速度增量超过300 m/s的情况下,中继应用轨道在空间中的位置变化较大,在z方向上的变化超过10 000 km,实际应用时,这一轨道变化可能会带来测控影响,如月球对中继应用通信的影响。不过从图4各平面投影图可见,轨道在各方向上与坐标原点的最小距离大于3 600 km,这表明月球不会形成直接遮挡,因而位置变化影响非常有限。尤其是由上述仿真可知,图4情况为极其特殊情况,一般情况下维持后的轨道不会有如此大的变化。

将仿真详细统计数据,与较小测控误差下的维持情况,以及较大测控误差下Az为30 000 km的中继应用轨道维持情况,列于表1所示。表1中ΔV、Δv、T和Δt分别为总速度增量、单次速度增量、轨道周期和维持间隔,每个参数分别给出最小值、最大值和平均值,上标b和s分别表示较大和较小的测控误差。由表1可见,在Halo控制方式下,对于小幅值中继应用轨道,如果测控精度提高,可以有效减小轨道维持代价。大幅值中继应用轨道的维持代价明显较大,说明Halo控制方式并不适用于大幅值轨道。

表1 中继应用轨道2年的维持情况(Halo方式)Table 1 Orbit maintenance of the relay orbit for 2 years(Halo style)

另外可见,大小幅值中继轨道的平均轨道周期均约为15 d左右,控制频率均约7 d左右。

2.2 Lissajous控制方式

利用Lissajous控制方式计算Az为5 000 km的Halo轨道维持1年的情况,进行100次蒙特卡洛打靶仿真,轨道维持间隔仍为1/2个轨道周期,延续控制最大时长为1圈,即使得第2次穿越xz平面时x和z方向速度小于1 m/s。总速度增量ΔVn和轨道周期Tnk变化如图5所示。

图5 较小测控误差下小幅值Halo轨道维持1年的情况(Lissajous方式)Fig.5 Orbit maintenance of the small Halo orbit for 1 years with the small TT&C errors(Lissajous style)

由图5可见,维持1年所需的速度增量均小于14 m/s,相对于Halo控制方式,维持速度增量大大降低。轨道周期依然呈现周期变化,不过变化幅值明显略有降低,保持在14～15.5 d之间。

维持速度增量最大的情况如图6所示。由图6可见,Lissajous控制方式维持后的轨道在z方向上的变化小于6 000 km,比Halo控制方式得到的轨道发散程度小。

将仿真统计数据,与较小测控误差下Az=30 000 km的中继应用轨道维持情况,列于表2所示。

表2 中继应用轨道1年的维持情况(Lissajous方式)Table 2 Orbit maintenance of the relay orbit for 1 year(Lissajous style)

由表2可见,在Lissajous控制方式下,大小幅值中继应用轨道的维持代价相当,均为十几米每秒,而且该方式的控后轨道与Halo控制方式的周期和维持频率基本相同。同时,将表2和表1对比可见,Lissajous控制方式明显优于Halo控制方式。

从目前国外在月球平动点轨道的维持应用来看,文献[10]中给出的ARTEMIS任务的最好仿真结果为12.27 m/s/a,平均为0.28 m/s,平均维持间隔为7.3 d,由此可见,本文给出的Lissajous轨道控制方式的维持代价与之相当。

此外还需指出,文章中的连续环绕轨道控制方法及其策略已经应用于我国“嫦娥2号”日地平动点拓展任务和“嫦娥5T1”拓展任务,基于文中方法得到的“嫦娥2号”中途修正速度增量仅为3.15 m/s,日地Lissajous轨道维持速度增量仅为3.19 m/s,维持间隔约3个月,控制效果非常好。

图6 较小测控误差下小幅值Halo轨道维持总速度增量最大的情况(Lissajous方式)Fig.6 Case with the maximum velocity increment of the small Halo orbit with the small TT&C errors(Lissajous style)

3 结 论

文章研究了月球平动点中继应用轨道的维持,在基于目前国内外测控能力的测控误差下,Lissajous轨道控制方式对平动点轨道的维持效果较好,轨道维持频率为大约每7.4 d维持一次,每年的维持速度增量可小于20 m/s,与国外ARTEMIS任务的维持代价相当。此外,需要说明,文章中轨道维持间隔相对固定,便于实际工程应用,若综合考虑地面测控和星载推力器能力,还可以进一步增大轨道维持间隔,降低维持频率。文章研究可直接应用于我国“嫦娥4号”和未来月球背面探测任务。

[1]Liu L,Liu Y,Cao J F,et al.CHANG’E-2 lunar escape maneuvers to the sun-earth L2 libration point mission[J].Acta Astronautica,2014(93):390-399.

[2]刘磊,刘勇,曹建峰,等.“嫦娥二号”探测小行星任务转移轨道设计[J].宇航学报,2014,35(3):262-268.[Liu L,Liu Y,Cao J F,et al.Mission design of the CHANG’E-2 asteroid exploration[J].Journal of Astronautics,2014,93:262-268.]

[3]Wu W R,Liu Y,Liu L,et al.Pre-LOI trajectory maneuvers of CHANG’E-2 libration point mission[J].Science in China Series F:Information Sciences,2012,55(6):1249-1258.

[4]乔栋,黄江川,崔平远,等.嫦娥二号卫星飞越探测小行星的目标选择[J].中国科学:技术科学,2013,43(6):602-608.[Qiao D,Huang J C,Cui P Y,et al.Target choice of the CHANG’E-2 asteroid exploration[J].Scientia Sinica Technologica,2013,43(6):602-608.]

[5]刘磊,唐歌实,胡松杰,等.月球探测再入返回试验后续飞行方案研究[J].宇航学报,2015,36(1):9-17.[Liu L,Tang G S,Hu SJ,et al.Follow-up flight scheme for the reentry test of china lunar exploration[J].Journal of Astronautics,2015,36(1):9-17.]

[6]Keeter T M.Station-keeping strategies for librationpoint orbits:target point and floquet mode approaches[D].West Lafayete,USA:Purdue University,1994.

[7]Kulkarni J,Campbell M.Asymptotic stabilization of motionabout an unstable orbit:application to spacecraft in halo orbit[C]∥Proceeding of the 2004 American Control Conference.Boston,Massachusetts:IEEE,2004:1025-1030.

[8]Moore A,Ober-Blöbaum S,Marsden J E.Optimization of spacecraft trajectories:a method combining invariant manifold techniques and discrete mechanics and optimal control[C]∥The 19th AAS/AIAA Spaceflight Mechanics Meeting.Savannah,Georgia:AIAA,2009.

[9]Howell K C,Pernicka H J.Numerical determination of Lissajous trajectories in the restricted three-body problem[J].Celestial Mechanics,1988,41:107-124.

[10]Folta D C,Woodard M A,Cosgrove D.Stationkeeping of the first earth-moon librationorbiters:the ARTEMIS mission[C]∥AAS11-515.[S.l]:AIAA,2011.

通信地址:北京5130信箱120#(100094)

电话:(010)66362455

E-mail:llbacc@139.com

Maintenance of Relay Orbit About the Earth-Moon Collinear Libration Points

LIU Lei1,2,CAO Jianfeng1,2,HU Songjie1,2,TANG Geshi1,2
(1.National Key Laboratory of Science and Technology on Aerospace Flight Dynamics Laboratory,Beijing 100094,China;2.Beijing Aerospace Control Center,Beijing 100094,China)

Relay orbits about the Earth-Moon collinear libration point shave significant valueon the exploration of the lunar farside,but have complex kinetic characteristics in the nature,thus the orbit maintenance has always been focused in the deep space navigation and control field.This paper explores orbit maintenance technology of the relay orbit about the collinear Earth-Moon libration points under the real dynamical conditions.First,based on the restricted three-body problem,the mathematic model of relay orbit station-keeping with the real dynamical model is analyzed.The continue-circling method is presented for the relay orbit maintenance with the two control styles,i.e.,the Halo style and the Lissajous style.Second,with the third-body gravitation and the solar radiation pressure perturbations considered,the method is tested and analyzed by using the numerical simulations to achieve the control frequency and the corresponding velocity increment required by the relay orbits with different amplitudes.According to the simulations,the Lissajous style is suitable to the orbit maintenance with a control interval of 7.4 days and a velocity increment less than 20 m/s/a.Furthermore,the method has been successfully applied in Chang’e-2 and Chang’e-5T1 extended missions and can provide a beneficial reference for the future Chang’e-4 mission.

libration point;orbit maintenance;restricted three-body problem;Halo orbit;Lissajous orbit

V412.4+1

A

2095-7777(2015)04-0318-07

10.15982/j.issn.2095-7777.2015.04.004

刘磊(1980—),男,工程师,主要研究方向:深空探测轨道设计与控制。

[责任编辑:宋宏]

2015-09-28

2015-10-20

国家自然科学基金资助项目(11303001,11203003,11373013,11173005,61573049)