严格对角占优M-矩阵最小特征值的新界

李艳艳,王东政

(1.文山学院数学学院,云南文山　663000;2.大连理工大学电子信息与电气工程学院,辽宁大连　116024)



严格对角占优M-矩阵最小特征值的新界

李艳艳1,王东政2

(1.文山学院数学学院,云南文山663000;2.大连理工大学电子信息与电气工程学院,辽宁大连116024)

摘要:利用严格对角占优M-矩阵A的逆矩阵A-1非主对角元素的估计式,首先给出了A-1的主对角元素的上下界,然后利用这个新界得到了最小特征值τ(A)的新估计式.理论证明和数值算例都说明新的估计式改进了李朝迁2013年给出的结果.

关键词:严格对角占优矩阵; M-矩阵; 最小特征值; 估计式;界

首先给出一些定义与记号:

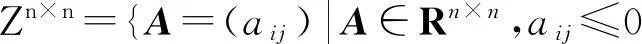
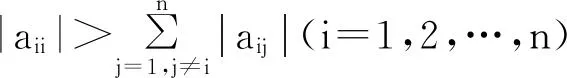
M-矩阵A分裂为A=D-C(D=diag(a11,a22,…,ann)),称JA=D-1C为A的迭代矩阵;

引理1[1]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则

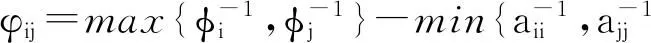
引理2[2]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则

引理3[2]设M=(βij)是非奇异的M-矩阵,N=(γij)是与M具有相同阶数的非负矩阵,N=M-A,则M-1N=JA,且满足如下不等式:

引理4[3]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则A-1=(αij)存在,且

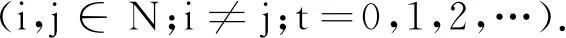
引理5[3]设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则∀i,j∈N,j≠i,t=0,1,2,…,如下两式成立:

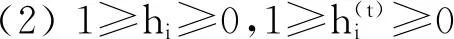
1　主要结果

下面首先利用行严格对角占优M-矩阵非主对角元素的估计式,给出主对角元素的上下界,然后给出最小特征值τ(A)的一些改进的下界.

定理1设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则A-1=(αij)存在,且

证明由引理4知,对任意的i∈N,t=1,2,…,有

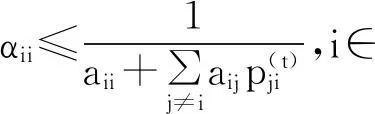
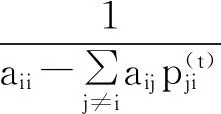
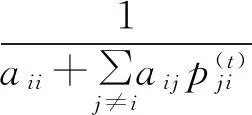
定理3设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则

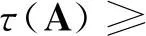
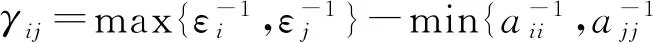
将上式代入引理2,有

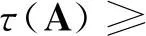
采用与定理3同样的方法可得如下定理.

定理4设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则

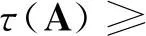
式中,}.

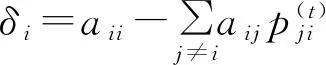
从而

即

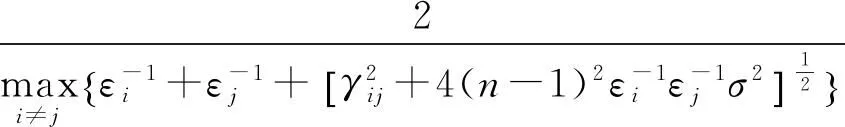
因此,式(6)提高了式(5),即定理4优于定理3.

推论设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则

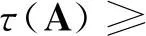
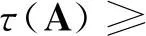
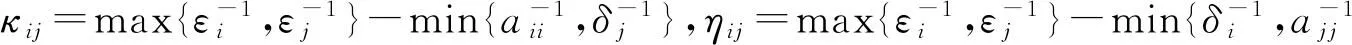
注3:由定理2知,当t=0,1,2,…时,式(5)～式(8)是严格单调递增的且以τ(A)为上界,因而该序列是收敛的.

如下定理利用了不等式证明的综合法[4],证明定理4提高了引理1.

定理5设A=(aij)∈Rn×n是行严格对角占优M-矩阵,则

τ(A)≥

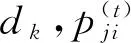
即

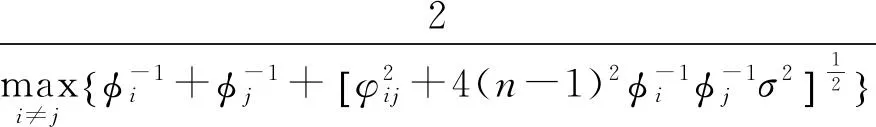
因为注1已经证明了

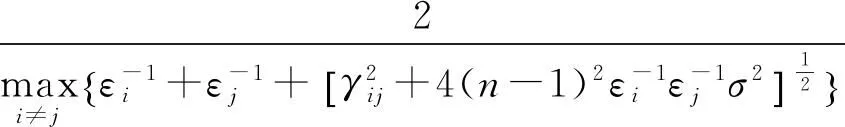
所以结合这两方面知结论成立.

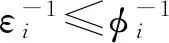
则

即推论中的式(7)、式(8)也提高了引理1.

2　数值算例

设

容易验证A是非奇异的M-矩阵,应用式(1)知τ(A)≥0.00688007.

应用本文的估计式知,当迭代次数t增大时,会得到逐步递增的下界.如表1所示.

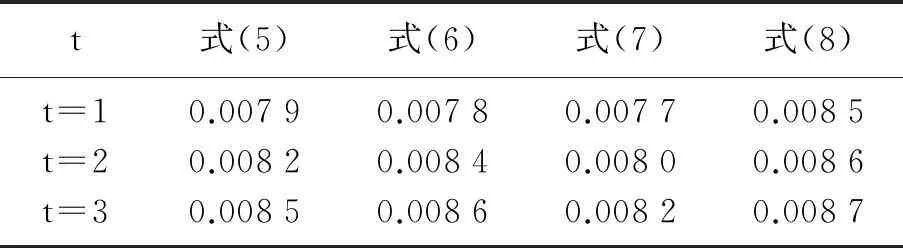
表1　应用估计式得到的下界

该算例进一步说明了本文估计式的有效性和可行性,并且这些新的估计式确实提高了文献[1]中的相应结果,故本文所得结论是对相关文献的一个有益补充.

参考文献:

[1]LiChaoqian,LiYaotang,ZhaoRuijuan.NewInequalitiesfortheMinimumEigenvalueofM-Matrices[J].LinearandMultilinearAlgebra, 2013,61(9):1267-1279.

[2]TianGuixian,HuangTingzhu.InequalitiesfortheMinimumEigenvalueofM-Matrices[J].ElectronicJournalofLinearAlgebra, 2010,20(3):291-302.

[3]赵建兴.M-矩阵(张量)最小特征值估计及其相关问题研究[D]. 昆明:云南大学, 2014:8-14.

(ZhaoJianxing.EstimationofMinimumEigenvalueofM-Matrix(tensor)anditsRelatedResearches[D].Kunming:YunnanUniversity, 2014:8-14.)

[4]王跃华,王洁英. 关于不等式几种常见证明方法的探究[J]. 沈阳大学学报:自然科学版, 2013,25(5):428-430.

【责任编辑:李艳】

(WangYuehua,WangJieying.SeveralCommonMethodsofProofofInequality[J].JournalofShenyangUniversity:NaturalScience, 2013,25(5):428-430.)

NewBoundsofMinimumEigenvalueofStrictlyDiagonallyDominantM-Matrix

Li Yanyan1,WangDongzheng2

(1.SchoolofMathematics,WenshanUniversity,Wenshan663000,China; 2.FacultyofElectronicInformationandElectricalEngineering,DalianUniversityofTechnology,Dalian116024,China)

Abstract:Using the estimators of the non-diagonally elements of strictly diagonally dominant M-matrix, the upper and lower bounds of the elements of the principal diagonal are given; secondly; using the new bounds, the new estimators of the minimum eigenvalue τ(A) are obtained. Theoretical proof shows new estimators improve the results given by Li Chaoqian in 2013, and numerical examples are presented to further verify the results.

Key words:strictly diagonally dominant matrix; M-matrix; minimum eigenvalue; estimator; bound

作者简介:李艳艳(1982-),女,甘肃庆阳人,文山学院讲师,硕士.

基金项目:国家自然科学基金资助项目(11361074);云南省教育厅科学研究基金资助项目(2013Y585);文山学院重点学科数学建设资助项目(No.12WSXK01).

收稿日期:2014-11-30

文章编号:2095-5456(2015)03-0255-04

中图分类号:O151.21

文献标志码:A