带有不可用区间、工件可拒绝的单机生产与运输协调调度问题

谢　谢,吴星瑶,李晓丽,孔祥玉

(1.沈阳大学装备制造综合自动化重点实验室,辽宁沈阳　110044;

2.浙江大学计算机科学与技术学院,浙江杭州310058;3.吉林省双辽市职业高级中学,吉林双辽136400)



带有不可用区间、工件可拒绝的单机生产与运输协调调度问题

谢谢1,吴星瑶2,李晓丽3,孔祥玉1

(1.沈阳大学装备制造综合自动化重点实验室,辽宁沈阳110044;

2.浙江大学计算机科学与技术学院,浙江杭州310058;3.吉林省双辽市职业高级中学,吉林双辽136400)

摘要:从生产实际提炼出一类单机生产与运输协调调度问题,即当工件在机器加工结束后由一辆容量受限的车运到配送中心.与经典调度问题不同的是,加工机器带有不可用区间,且可以拒绝加工某些工件,但拒绝产生惩罚.目标函数是最后一批完工工件到达配送中心的时间与拒绝工件的惩罚和.由于该问题是NP-难的,提出了一个多项式时间内可解的启发式算法,并证明该算法的最坏性能比为6.

关键词:调度; 不可用区间; 拒绝工件; 启发式算法

传统的生产调度和运输调度是分开研究的,通常都是将生产放在首要位置而运输放在一个从属的地位,即先安排生产调度,然后再相应进行运输物流调度.然而在实际生产中,由于运输工具数量和能力的限制,而使工序之间物料的传递受到了限制,在不考虑运输情况的生产调度即使是最优调度也难以有效的执行.所以将生产调度和运输物流调度协调进行研究,有助于提高运输工具的利用率,使得生产与运输之间的时间衔接更加精确,从而有效地降低生产和运输的物流总费用.此外,生产调度问题在过去的几十年中,大多都是假设机器可以连续运作,同时所有工件都必须接受加工.然而,由于生产过程的突发等非确定性因素,往往导致机器不能连续运作.同时生产商考虑到企业的现有资源往往会将一些工件采用外包的方式而拒绝加工,外包的同时要支付一定的外包费用.因此,本文从生产实际提炼出一类单机生产与运输协调调度问题,生产阶段有一台加工机器,机器带有不可用区间、工件加工可以被拒绝,但拒绝产生惩罚.当工件加工完成后被运输阶段的一台车运往指定的配送中心,该车辆每次最多可装载K个工件.目标函数为最小化最后一批完工工件到达配送中心的时间与拒绝工件惩罚和.

有关生产与运输协调调度问题首次由Hall和Potts[1]提出,其中运输的方式可以是直接的运输方式或考虑路径优化的运输方式,同时运输阶段考虑了原材料的供给与产成品的配送.在Hall和Potts的基础上,Chang和Lee[2]考虑了加工后的工件具有不同的物理大小,所以在运输的过程将考虑装箱问题,并且假设运输的目的地的地理位置不同,针对此类问题他们提出一个启发式算法并给出最坏性能分析.He等[3]考虑了单机生产与运输协调调度问题,且运输过程仅由一辆车辆完成,目标函数是最小化工件最大完工时间,即最后一个加工完成的工件到达客户指定位置且车辆返回加工中心的时间,通过提出一个启发式算法求解,并证明该算法的最坏性能为5/3.Wang和Cheng[4]考虑了生产与运输协调调度问题,在生产环节机器带有不可用区间,且车辆的最大容量为k个工件,目标函数是最大完工时间,这里最大完工时间是指最后一批加工完成的工件到达配送中心的时间,首先证明此类问题为NP-难的,然后提出启发式算法求解并证明最坏性能分析.

工件可拒绝的调度问题首次被Bartal等[5]提出,目标函数是最小化加工工件的最大时间表长与拒绝工件惩罚和,采用设计全多项式时间近似方案(FPTAS)求解.后来,Zhang等[6]考虑了工件可拒绝的单机调度问题,且每个工件带有不同的释放时间,目标函数是最小化加工工件的最大完工时间与拒绝工件惩罚和,采用启发式算法求解,并证明该算法的最坏性能为2,为了使得问题可以在多项式时间内求得近似解,最后设计一个全多项式时间近似方案(FPTAS),此方案的运算时间是O(n3/ε).

机器带有不可用区间的调度问题首次由Adiri等[7]提出,分别针对具有确定的不可用区间和随机性的不可用区间两种情况进行分析,目标函数是最小化工件的总完工时间和,首先证明此类问题为NP-难的,同时证明应用经典的SPT算法求解的最坏性能为2/7.后来,Kacem和Mahjoub[8]考虑了带有不可用区间的单机调度问题,目标函数是工件的总完工时间和,尝试设计一个全多项式时间近似方案(FPTAS)求解,使得问题可以在多项式时间内求解.Kacem和Kellerer[9]考虑了带有不可用区间的单机调度问题,且每个工件都有不同的释放时间,考虑到问题的复杂性,采用启发式算法求解,并证明该算法的最坏性能为2.由此看出,大多数学者针对带有不可用区间或工件可拒绝的调度问题的研究,很少有人将不可用区间工件可拒绝两种约束同时考虑.

结合以上文献可以看出,大多数学者仅考虑运输阶段的各种限制,很少考虑生产阶段的约束,或者仅考虑生产阶段的约束而没有将运输一起考虑,如谢等[10].因此,本文考虑一类带有不可用区间、工件可拒绝的生产与运输协调调度问题,针对该问题的复杂性,提出了多项式时间内求解问题的启发式算法,并进一步证明了该算法的最坏性能比为6.

1　问题参数及描述

问题描述如下:给定n个工件的集合N={J1,J2,…,Jn}.要求接收加工的工件首先在机器上加工,加工完成后运往配送中心.在工件的生产阶段存在两种约束:①生产商考虑到自己的利益,在安排生产之前可能会拒绝某些工件的加工,但相应需要支付一定惩罚;②机器在加工的过程中由于定期维护带来一段时间不可用.不失一般性本章涉及的所有参数都为正整数,各参数如下:

pj为工件Jj的加工时间;

wj为工件Jj的拒绝惩罚值;

[T1,T2]为机器由于维修、保养带来的一段作业时间受限区间;

Δ=T2-T1为机器受限时间间隔;

σ为工件集N的一个可行排序即工件的加工顺序;

Bk为第k次配送批次;

α(Bk)为配送批次Bk的最后一个工件的加工完成时间;

C(Bk)为车辆返回加工中心准备运输Bk的时间;

q1和q2有n=Kq1+q2,且q1和q2为整数,0≤q2≤K;

φ=[B1,B2,…,Bm],运输方案q1+1≤m≤n;

(σ,φ)为生产与运输调度的可行方案;

C(σ,φ)为(σ,φ)的最后一批工件运送到配送中心且车辆返回加工中心的最大完工时间;

C*(σ,φ)为最优方案的最大完工时间;

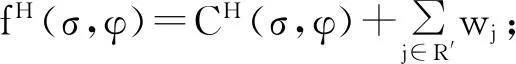
2　启发式算法及最坏性能分析

为了较快的得到较好的近似解,给出如下满足最优解的性质以加快解的搜索过程:

①工件加工尽可能早,且加工无空闲;②先加工完的工件先运输;③当有K个工件加工完时车辆的运输不能空闲必须立即运往配送中心.

(2) 对于一个最优调度方案,满批运输方案一定最优,即q1+1=m且|B1|=q2,|B2|=…=|Bq+1|=K.

(3) 对于已经分批的工件,早加工完成的配送批先运输.

根据以上性质,启发式算法H的具体步骤如下:

第1步按照SPT规则即按pj不减的顺序对工件进行加工,并将其可行排序记为σ1.

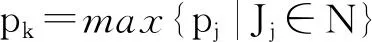
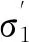
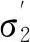
第5步按照性质5、6对第一步与第二步的工件确定运输方案,将分别产生两个运输方案φ1,φ2.

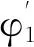
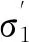
由于第1步运算的时间为O(nlogn),且为该算法的主要步骤,因此,该算法的运算时间为O(nlogn).

又因为wj≤pj,所以有

因此,所提出的启发式算法的最坏性能比为6.

3　结　　论

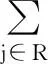
参考文献:

[1]HallNG,PottsCN.SupplyChainScheduling:BatchingandDelivery[J].OperationResearch, 2003,51(4):566-583.

[2]ChangYC,LeeCY.MachineSchedulingwithJobDeliveryCoordination[J].EuropeanJournalOperationResearch, 2004,158(2):470-487.

[3]HeYong,ZhongWeiya,GuHuikun.ImprovedAlgorithmsforTwoSingleMachineSchedulingProblems[J].TheoreticalComputerScience, 2006,363(3):257-265.

[4]WangXL,ChengTCE.MachineSchedulingwithanAvailabilityConstraintandJobDeliveryCoordination[J].NavalResearchLogistics, 2007,54(1):11-20.

[5]BartalY,LeonardiS,SpaccamelaAM,etal.Multi-ProcessorSchedulingwithRejection[J].SIAMJournalonDiscreteMathematics, 2000,13(1):64-78.

[6]ZhangLQ,LuLF,YuanJJ.SingleMachineSchedulingwithReleaseDatesandRejection[J].EuropeanJournalofOperationResearch, 2009,198(3):975-978.

[7]AdiriI,BrunoJ,FrostigE,etal.SingleMachineFlow-TimeSchedulingwithaSingleBreakdown[J].ActaInformatica, 1989,26(7):679-696.

[8]KacemI,MahjoubAR.FullyPolynomialTimeApproximationSchemefortheWeightedFlow-TimeMinimizationonaSingleMachinewithaFixedNon-AvailabilityInterval[J].ComputersandIndustrialEngineering, 2009,56(4):1708-1712.

[9]KacemI,KellererH.FastApproximationAlgorithmstoMinimizeaSpecialWeightedFlow-TimeCriteriononaSingleMachinewithaNon-AvailabilityIntervalandReleaseDates[J].JournalofScheduling, 2011,14(3):257-265.

[10]谢谢,李晓丽,孔祥玉. 带有不可用区间、工件可拒绝的单机调度问题[J]. 沈阳大学学报:自然科学版, 2015,27(1):34-39.

【责任编辑:胡天慧】

(XieXie,LiXiaoli,KongXiangyu.SingleMachineSchedulingProblemwithUnavailabilityIntervalandRejection[J].JournalofShenyangUniversity:NaturalScienceEdition, 2015,27(1):34-39.)

ProductionandTransportationCoordinatedSingleMachineSchedulingProblemswithUnavailabilityIntervalandRejection

Xie Xie1,WuXingyao2,LiXiaoli3,KongXiangyu1

(1.KeyLaboratoryofManufacturingIndustrialandIntegratedAutomation,ShenyangUniversity,Shenyang110044,China; 2.CollegeofComputerScienceandTechnology,ZhejiangUniversity,Hangzhou310058,China; 2.ShuangliaoVocationalHighSchoolofJilinProvince,Shuangliao136400,China)

Abstract:A production and transportation coordinated single machine scheduling problem is abstracted from practical production, which is, the workpieces can be transported to the distribution center by a capacity constrained vehicle after machining. Different from the classical scheduling problem, the processing machine has unavailable interval and rejection, and can refuse to produce punishment. The objective function is the sum of the arrival time of last delivery batch to the distribution center and penalties of the rejected jobs. For the problem is NP-hard, a polynomial time solvable heuristic algorithm is proposed, and further demonstrate the worst case bound 6. It is proved that the algorithm’s worst-case performance ratio is 6.

Key words:scheduling; unavailable interval; rejection job; heuristic algorithm

作者简介:谢谢(1981-),女,辽宁沈阳人,沈阳大学副教授,博士.

基金项目:国家自然科学基金资助项目(71201104);辽宁省高等学校杰出青年学者成长计划项目(LJQ2014133).

收稿日期:2014-12-23

文章编号:2095-5456(2015)03-0222-04

中图分类号:TP30

文献标志码:A