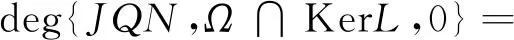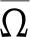离散Lotka-Volterra偏害模型周期正解的存在性

陈凤德,张茂石,韩荣玉

(福州大学数学与计算机科学学院,福建福州　350116)



离散Lotka-Volterra偏害模型周期正解的存在性

陈凤德,张茂石,韩荣玉

(福州大学数学与计算机科学学院,福建福州350116)

摘要:研究了一类非自治离散Lotka-Volterra偏害模型,借助重合度理论得到了一组保证系统存在周期正解的充分性条件.

关键词:偏害作用; 重合度; 周期正解

1　预备知识

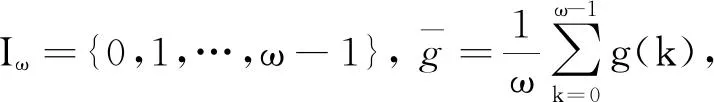
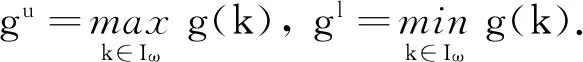
借助向量场分析的方法研究了系统(2)的轨线走向问题.式中,x≥0,y≥0,a1>0,a2>0,b1<0,c1<0,c2<0均为常数. 最近,韩荣玉等[6]认为生态系统是随着季节变化而变化的,故需要考虑时变的非自治系统,他们提出了如下两种群偏害关系模型:

(3)

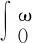
如文献[3]所言,对生命短、世代不重叠的种群,或者虽然是生命长、世代重叠的种群, 但在其数量比较少时,用差分方程(或者说离散动力模型)来表示更为合理. 因此,本文提出了与系统(3)相对应的离散的两种群偏害模型:

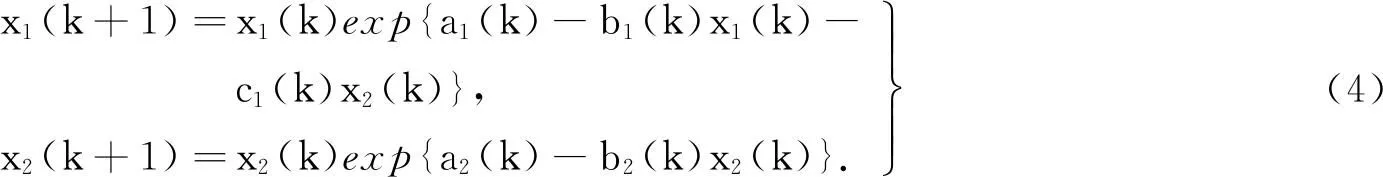
2　主要结果

为了证明周期正解的存在性, 引入重合度理论中的延拓定理.

(a) 对任意的λ∈(0,1),方程Lx=λNx的解满足x∉∂Ω∩domL,

(b) 对任意的x∈∂Ω∩KerL,QNx≠0而且deg{JQN,Ω∩KerL,0}≠0,

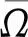
引理3[8]设g:Z→R为ω-周期序列,即g(k+ω)=g(k),则对任意固定的k1,k2∈Iω及k∈Z,有：

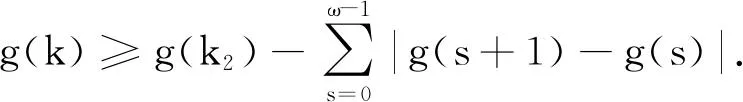
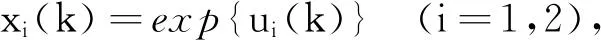
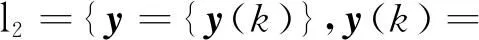
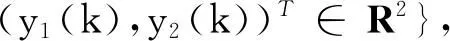
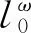
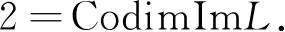
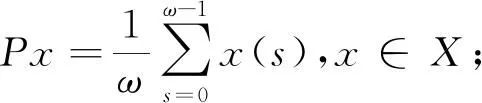
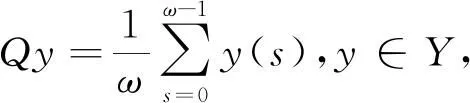
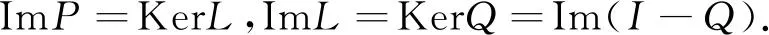
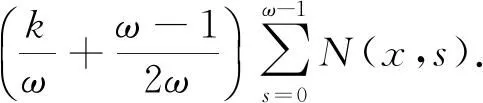
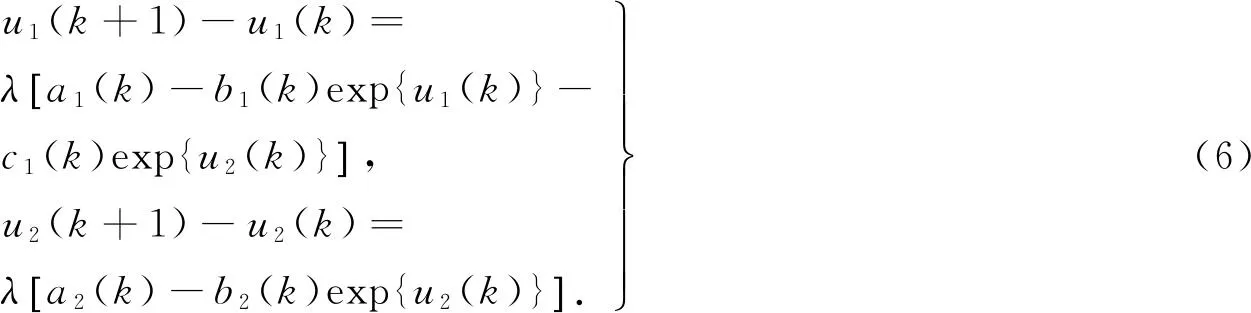
设u=u(k)∈X是系统(6)的对应于某个λ∈(0,1)的解,将式(6)两端同时从0到ω-1关于k求和,得到:

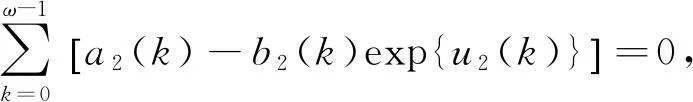
由式(7)和式(8),有

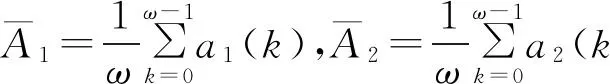
由式(8)有

即

从而由式(9)、式(11)和引理3可得

由式(8)也有

即

从而由式(9)、式(13)和引理3可得

由式(12)和式(14)有

由式(7)有

由此可知

从而由式(9)、式(16)和引理3可得

由式(7)和式(12)也有

注意到定理的条件,有

于是

从而有

由式(17)和式(19)有

显然,Hi(i=1,2)的选取与λ的选取无关.由定理的已知条件知,代数方程组

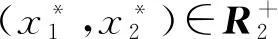
令H=H1+H2+H3,其中,H3>0充分大,使得

令

Ω={u(k)=(u1(k),u2(k))T∈X:‖u‖

则Ω满足引理1中的条件(a).当u∈∂Ω∩KerL=∂Ω∩R2时,u是R2中的常值向量且‖u‖=H,于是

因为式(21)存在唯一的正解,由已知条件直接计算知

注定理表明: 当第一个种群的内禀增长率足够大、第二个种群的种内密度制约因素足够大而内禀增长率不大(这表明第二个种群的种群数量不可能太大,从而其对第一个种群的影响也就有限)时,两个种群能以周期震荡的形式共存.

参考文献:

[1]王海娜,陈凤德,陈婉琳,等. 具有反馈控制的非自治两种群浮游生物相克系统的持久性和全局吸引性[J]. 沈阳大学学报:自然科学版, 2013,25(3):173-176.

(WangHaina,ChenFengde,ChenWanlin,etal.PermanenceandGlobalAttractivityofNon-AutonomousAllelopathicPhytoplanktonModelforTwoSpecieswithFeedbackControls[J].JournalofShenyangUniversity:NaturalScience, 2013,25(3):173-176.)

[2]林玉花,陈凤德,王海娜,等. 一类非自治两种群浮游生物相克模型的持久性和全局吸引性[J]. 沈阳大学学报:自然科学版, 2012,24(6):7-10.

(LinYuhua,ChenFengde,WangHaina,etal.PermanenceandGlobalAttractivityofaNon-AutonomousTwoSpeciesAllelopathicPhytoplanktonModel[J].JournalofShenyangUniversity:NaturalScience, 2012,24(6):7-10.)

[3]陈凤德,谢向东. 合作种群模型动力学研究[M]. 北京: 科学出版社, 2014.

(ChenFengde,XieXiangdong,StudyontheDynamicBehaviorsofCooperativePopulation[M].Beijing:SciencePress, 2014.)

[4]孙广才. 两种群偏害作用模型的定性分析[J]. 佳木斯大学学报:自然科学版, 2003,21(3):283-286.

(SunGuangcai.QualitativeAnalysisonTwoPopulationsAmensalismModel[J].JournalofJiamusiUniversity:NaturalScienceEdition, 2003,21(3):283-286.)

[5]祝占法,陈巧灵. 偏害关系的Lotka-Volterra模型的数学研究[J]. 鸡西大学学报, 2008,8(5):100-101.

(ZhuZhanfa,ChenQiaoling.MathematicalAnalysisonCommensalismLotaka-VolterraModelofPopulations[J].JournalofJixiUniversity, 2008,8(5):100-101.)

[6]韩荣玉,薛亚龙,杨丽娅,等. 具有偏害关系的L-V模型周期正解的存在性[J]. 龙岩学院学报, 2015(2).

(HanRongyu,XueYalong,YangLiya,etal.GlobalExistenceofPositivePeriodicSolutionofaNonautonomousTwoPopulationsAmensalismModel[J].JournalofLongyanUniversity, 2015(2).)

[7]GainesRE,MawhinJL.CoincidenceDegreeandNonlinearDifferentialEquations[M].Berlin:Springer-Verlag,1977:40.

[8]FanM,WangK.PeriodicSolutionsofaDiscreteTimeNonautonomousRatio-DependentPredator-PreySystem[J].MathematicalandComputersModelling, 2002,35(9/10):951-961.

【责任编辑:李艳】

ExistenceofPositivePeriodicSolutionofaDiscreteLotka-VolterraAmensalismModel

Chen Fengde, Zhang Maoshi, Han Rongyu

(CollegeofMathematicsandComputerScience,FuzhouUniversity,Fuzhou350116,China)

Abstract:A non-autonomous discrete Lotka-Volterra amensalism model is studied. By using a theorem of coincidence degree, a set of sufficient conditions which guarantee the global existence of positive periodic solutions of the system is obtained.

Key words:amensalism model; coincidence degree; positive periodic solution

作者简介:陈凤德(1974-),男,福建屏南人,福州大学教授.

基金项目:国家自然科学基金资助项目(11201075,11361068);福建省自然科学基金资助项目(2013J01011).

收稿日期:2015-01-20

文章编号:2095-5456(2015)03-0251-04

中图分类号:O175.14

文献标志码:A