一种改进的OMP高光谱稀疏解混算法

赵春晖,肖健钰,齐　滨

(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨　150001)



一种改进的OMP高光谱稀疏解混算法

赵春晖,肖健钰,齐滨

(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001)

摘要:正交匹配追踪算法是稀疏求解中常用的方法,用于噪声影响下的高光谱数据稀疏解混时,其解混效果不理想.针对这一问题,提出了全约束DOMP算法.通过引入广义Dice系数代替内积作为匹配度量准则,更充分地利用了光谱信息,提高了算法的抗噪能力.同时,为了满足丰度的“非负”及“和为1”的性质,对丰度系数进行了全约束,进一步改善了解混效果.模拟及真实数据仿真结果显示,改进算法明显提高了解混精确度,验证了算法的有效性.

关键词:高光谱图像; 稀疏解混; 正交匹配追踪; 广义Dice系数; 丰度约束

随着遥感技术的发展,高光谱遥感图像在越来越多的领域中得到应用.由于受到大气传输混合效应、地物复杂度、高光谱成像仪的空间分辨率较低等因素的影响,混合像元在高光谱数据中大量存在,严重阻碍了高光谱图像的应用及发展[1].因此,高光谱图像混合像元分解技术的研究,对于高光谱遥感技术的进一步发展具有重要意义.线性光谱解混算法通常分为端元提取和丰度反演两个步骤,先通过端元提取算法找到纯像元,再利用端元提取得到的端元光谱信息进行丰度反演.近年来,Iordache和Dias等将稀疏的思想引入高光谱解混算法[2],用光谱库代替线性光谱混合模型中的端元矩阵,使混合像元在光谱库下的丰度向量具有稀疏性,这种利用稀疏性的解混算法称为稀疏解混算法[3].这类算法的优势是无须假设纯像元的存在,避免了端元提取这一步骤可能引入的误差.代表性的稀疏解混算法有Dias等提出的SUnSAL算法[4]及其改进的SUnSAL-TV算法[5],Iordache等提出的OMP、ISMA[6],史振威等提出的SMP[7]等匹配追踪类算法[8].

正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法用于稀疏解混,可保证每次迭代后光谱库的端元集与混合像元残差光谱正交,从而获取最优解[9].然而,当高光谱数据受噪声影响较大时,基于OMP的稀疏解混算法的丰度反演效果并不理想.针对这一问题,本文提出了全约束DOMP稀疏解混算法,用广义Dice系数法[10]代替内积作为光谱匹配准则,并对丰度系数加入了“非负”及“和为1”的全约束,使其满足丰度的约束条件.为验证改进算法的有效性,本文利用合成高光谱数据及真实的高光谱遥感试验区农田数据进行了高光谱解混仿真实验.

1　基于OMP的稀疏解混算法

1.1稀疏的线性光谱混合模型

基于稀疏的高光谱解混算法,引入了一个有效的光谱库,并将观测到的光谱曲线表示成光谱库中各地物的线性组合的形式[11].该方法与传统的高光谱解混算法相比,不需要假设纯像元的存在,避免了端元提取步骤可能带来的误差.同时,丰度反演的效果不再取决于高光谱图像中是否存在纯像元,而是如何从光谱库中找到可以线性表示混合像元的最优子集[12].

高光谱稀疏解混问题可以理解为已知一个过完备光谱库的情况下,寻找方程最简单解的问题.用D表示成像光谱仪采集到的光谱库,将高光谱图像中的像元x表示为光谱库D中各光谱响应曲线线性组合的形式,得到如下基于稀疏的线性光谱的混合模型:

式中,高光谱图像中的像元x∈L×1,光谱库矩阵D∈L×p,α表示丰度系数,n为误差项,L为波段数,p为光谱库D中所包含的光谱曲线的数目.

由于α是稀疏的,可以将式(1)等价为一个l0范数最小化问题,则有:

式中,‖·‖0表示l0范数,代表丰度向量α中非零元素的个数.实际应用中,涉及建模、噪声等原因,可能会存在一定的误差.因此,将式(3)用不等式约束形式来表示:

式中,δ表示极小的常量.

l0范数的优化问题是一个NP难问题,需要通过遍历寻找全局最优解.匹配追踪类算法是解决这类问题的主要方法.OMP算法每次迭代后的混合像元残差与端元集正交[13],具有每次迭代都能快速找到最优解、算法复杂度较低的优势,是一种较为经典的高光谱稀疏解混算法.

1.2传统的OMP稀疏解混算法

OMP稀疏解混算法利用迭代的方式实现了混合像元光谱的重构.用内积度量光谱匹配度,根据光谱匹配程度,从光谱库中选取用来表示混合像元的端元,构造混合像元光谱的稀疏线性逼近[14].每次迭代能保证选择的端元与当前混合像元光谱残差有最大的相关性,同时能保证混合像元残差光谱与从光谱库中选出的端元集正交,并不断地更新残差向量,当迭代次数为稀疏度N时,停止迭代.具体来说,OMP稀疏解混算法的流程如下.

输入:光谱库D=[d1,d2,…,dp],混合像元x,稀疏度N.

初始化:r0=x,索引集Λ0=∅,循环次数k=1.

过程:在第k次循环中

(1) 利用内积计算获得相关的端元索引:

(2) 获得的端元索引加入索引集:

(3) 更新残差:

(4)k=k+1,返回步骤(1),直到达到迭代终止条件:循环次数k=N;

从OMP稀疏解混算法流程中可以看到,残差rk始终正交于DΛk,所以在迭代寻优过程中,每次迭代,OMP算法都会寻找到新的匹配端元,端元不会被重复地找到,具有较高的收敛速度,缩短了计算时间.

2　OMP稀疏解混的改进算法

2.1DOMP稀疏解混算法

对OMP稀疏解混算法的研究可知,从光谱库中选出最佳匹配端元与混合像元残差项匹配的步骤在稀疏解混算法中起到了重要作用.如果最佳匹配端元的选取不够准确,那么必然影响丰度反演的最终效果.用内积作为匹配准则,只考虑了混合像元残差项光谱与光谱库端元光谱的相关性,光谱内其他信息没有得到体现.当高光谱数据受到噪声等外界因素影响较大时,仅利用相关性作为光谱匹配程度的度量可能会导致端元选取不合理.为了进一步提高OMP稀疏解混算法的性能,本文采用更优的端元选取方法,用广义Dice系数法代替常用的内积度量光谱匹配程度.内积度量端元和混合像元残差项光谱相似性的公式如下:

由于内积度量光谱匹配程度时,更多考虑地是光谱的相关性,光谱中的其他信息也没有得到显著放大.为了更好地利用光谱信息,本文提出如下Dice系数准则度量光谱匹配程度公式:

式中,r∈L×1表示混合像元残差项光谱,d∈L×1表示光谱库中的一条端元光谱曲线,L表示波段数.与式(5)相比,式(6)考虑了光谱的算术平均值,更能够突出光谱本身包含的信息,所以Dice系数准则能够更加准确地从光谱库中挑选出合适的端元与残余光谱匹配.当高光谱数据受噪声影响较大时,混合像元残差项光谱与端元光谱算术平均值的加入,也可以一定程度上对噪声起到抑制作用,因此,该算法在信噪比低的情况下具有更好的高光谱解混效果.本文将这种以Dice系数作为光谱匹配准则的稀疏解混算法称为DOMP稀疏解混算法.同时,由于DOMP算法与OMP算法相比仅改变了光谱库与混合像元残差光谱的匹配准则,因此仍然具有收敛性.

2.2全约束的DOMP稀疏解混算法

传统的OMP稀疏解混算法未进行丰度约束,计算得到的丰度系数中包含负数,且每个像元的丰度系数的和不为1.由于丰度系数表示的是高光谱混合像元中各地物所占的比例,应该满足“非负”及“和为1”的约束[14].传统的OMP稀疏解混算法得到的丰度系数不满足丰度的约束条件,必然导致最终的反演效果不理想.因此,本文提出了全约束的DOMP稀疏解混算法,使得最终得到的丰度系数满足丰度的约束条件.在式(1)的基础上,可以得到基于稀疏的线性光谱混合模型的非负模型及全约束模型,如下所示:

式中,x表示高光谱图像中的一个像元,D表示光谱库矩阵,α是丰度系数矩阵,αi表示光谱库中的i端元在混合像元对应的丰度系数,n为误差项,p为光谱库D中所包含的光谱曲线的数目.

为了在改进算法中实现丰度约束,考虑将丰度约束最小二乘算法的思想引入残差更新的计算中.对于全约束的DOMP算法,采用全约束最小二乘算法对信号进行逼近,更新残差项公式修改为

全丰度系数输出为

为了保证混合像元残差光谱与光谱库的端元光谱正交,需要将进行全约束后得到的残差光谱投影到端元索引集DΛk的正交子集上.具体公式如下:

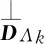
由于某些高光谱解混算法中丰度系数加入非负约束与加入全约束的解混效果相近,为了提高运算速度,可以只考虑丰度的非负性,因此,本文对非负约束的DOMP算法也进行了研究,并同FDOMP算法进行了分析比较.

类似地,采用非负约束最小二乘算法对信号进行逼近,更新残差项公式修改为

非负约束丰度系数输出为

2.3FDOMP稀疏解混算法流程

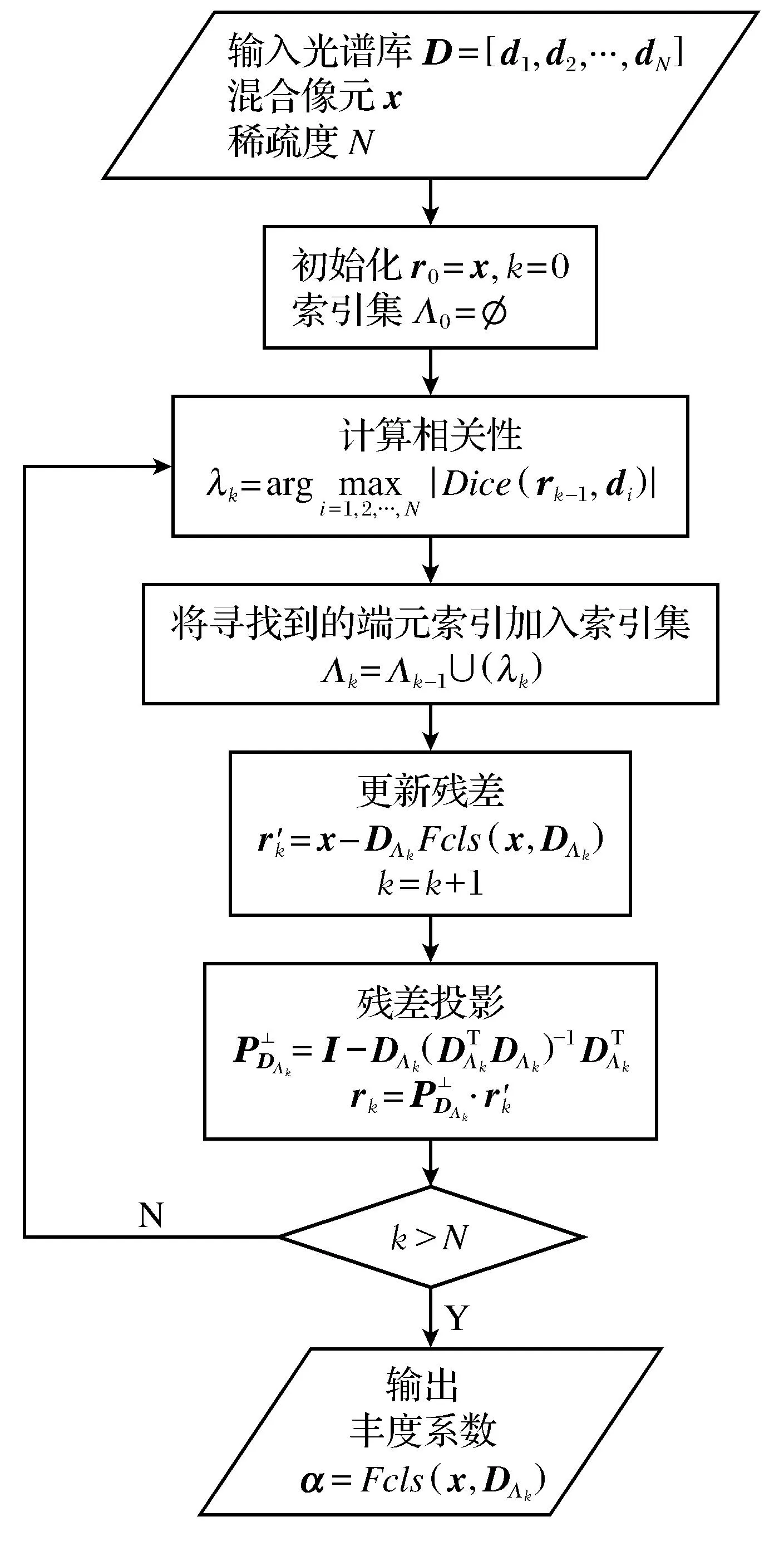
图1　FDOMP算法流程图

3　仿真实验分析

关于高光谱解混效果的评价指标很多,基于稀疏的混合像元分解方法通常采用丰度的均方根误差来衡量解混效果[15].根据定义,每个端元的丰度均方根误差如下式所示:

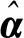
3.1模拟数据仿真实验及分析

模拟数据的光谱库是从美国地质勘探局USGS的光谱库中选择光谱角较大的60条光谱曲线生成的.这些光谱曲线包括224个波段,均匀分布在0.4～2.5μm之间.从光谱库中选择铵长石、高岭石、白云母3种矿物的光谱曲线作为端元,分别编号1、2、3,根据丰度系数的“非负”及“和为1”的性质构造丰度系数矩阵,并生成高光谱混合像元模拟数据.应用传统的OMP算法及DOMP、NDOMP、FDOMP算法对高光谱混合像元模拟数据进行实验仿真,以验证FDOMP算法的有效性.分别添加信噪比为20、25、30、35、40dB的高斯噪声,计算丰度反演算法丰度的RMSE值,具体实验结果如表1所示.

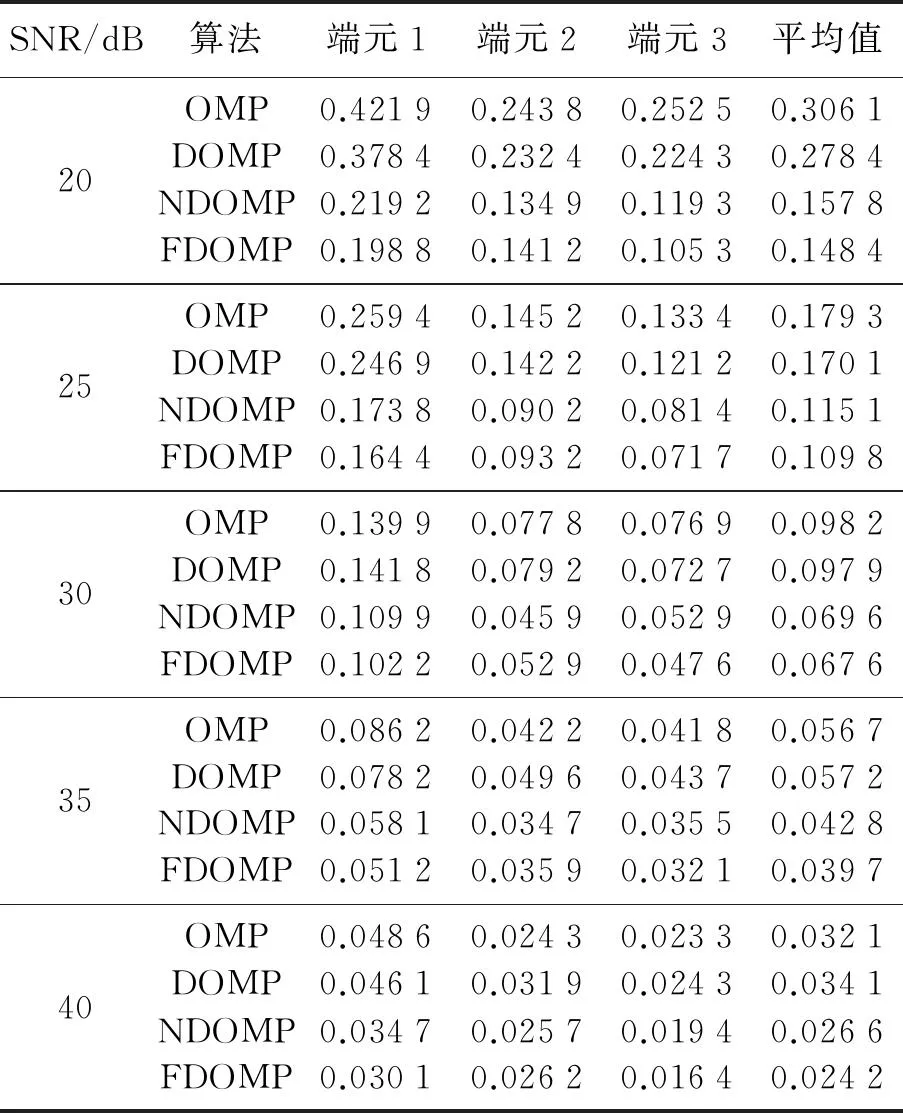
表1中记录了3种地物端元在不同信噪比下,各稀疏解混算法得到的丰度RMSE值,同时记录了每种算法在不同信噪比下的丰度的平均RMSE值.分析实验结果可知,在不同信噪比的情况下,全约束的DOMP算法都对反演效果有较大的改善.同时,在低信噪比的情况下,DOMP与OMP算法相比,获得的丰度值更接近真实结果,验证了DOMP算法的抗噪性能.由于DOMP算法在进行混合像元光谱与光谱库中的端元光谱匹配时,不仅关注光谱间的相关性,更考虑到了光谱本身包含的信息,因此在噪声较大的条件下获得了更好的反演效果.FDOMP算法在DOMP算法的基础上加入了全约束,使丰度值满足“非负”及“和为1”的性质,反演效果应该会得到大幅度的提升,仿真实验结果也验证了这一点.通过比较FDOMP与NDOMP的RMSE值,FDOMP算法的丰度的误差更小,因此,加入“和为1”的约束在本算法中是有意义的.随着信噪比的增加,改进算法的优势逐渐减小.在信噪比较高的条件下,OMP算法及改进算法的稀疏解混效果都比较好,但改进算法仍更具优势.

图2是不同信噪比下各稀疏解混算法丰度的平均RMSE值.从图2中可以更直观地看到,FDOMP改进算法的解混精度显著提高.同时,在噪声较高的情况下,DOMP与OMP算法相比,效果改进比较明显.FDOMP与NDOMP算法相比,丰度的平均RMSE值更低,得到的丰度值更接近真实值,因此,本文提出的算法采用全约束很有必要.

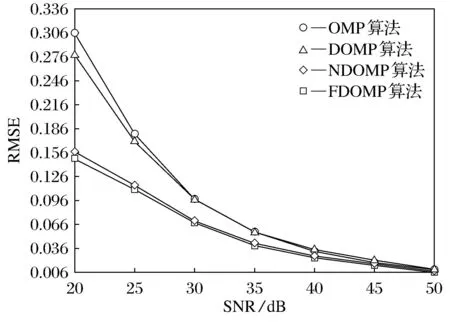
图2　 不同信噪比下稀疏解混算法丰度的

图3从正确反演混合像元数目的角度,对比了不同算法的解混效果.图3中显示了信噪比为30dB时混合像元的丰度误差,横轴表示丰度的RMSE值,纵轴表示混合像元的个数.RMSE值在0.1以下的混合像元的个数越多,说明正确反演的像元数越多,解混效果越好.从图3中可以看出,本文提出的FDOMP算法大部分混合像元的丰度RMSE值在0.1以下,并且有大量像元的RMSE值接近0,即大部分像元解混得到的丰度与真实丰度非常接近.FDOMP算法同传统的OMP算法相比,正确反演的像元个数具有明显优势.DOMP算法得到的丰度RMSE值在0.05以下的混合像元数比OMP算法更多,正确反演的像元数也比OMP算法多.同时,将本文提出的算法与NDOMP算法相比,混合像元正确反演方面明显更具有优势.本实验通过分析每个混合像元的丰度误差,再次说明了改进算法在丰度反演效果上的明显提升.

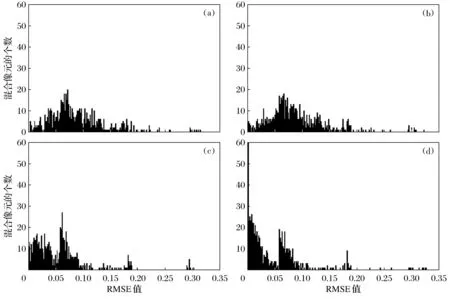
图3　模拟数据像元的丰度RMSE值

为了更直观地观察稀疏解混算法得到的每个端元对应的丰度向量的准确程度,采用生成丰度图像的方式比较解混效果.图4是合成数据三个端元对应的真实的丰度图像,作为其他稀疏解混算法丰度图像的对比图.图5~图8分别为OMP、DOMP、NDOMP、FDOMP稀疏解混算法在信噪比为40dB时得到的丰度图像.图5的OMP稀疏解混算法与图6的DOMP稀疏解混算法丰度图上的解混效果相近,但DOMP算法端元1和端元3的丰度图层次更清晰,更加接近真实的丰度图像.图8中,FDOMP稀疏解混算法除个别丰度值外,与真实丰度图像非常相近,较传统的算法效果改善明显,再次证明了全约束DOMP算法的有效性.通过分析解混丰度图,可以直观地观察到,改进算法的丰度反演结果更准确.当信噪比不断降低时,也可以通过丰度图观察到改进算法的优势更加明显.

图4　模拟数据真实的丰度图像

图6　DOMP算法解混的丰度图像

图7　NDOMP算法解混的丰度图像

图8　FDOMP算法解混的丰度图像

3.2真实数据仿真实验及分析

为了验证本文提出的改进算法在实际应用中的有效性,采用真实的AVIRIS高光谱遥感图像进行仿真实验.该图像数据是于1992年6月在美国印第安纳州西北部印第安遥感试验区拍摄得到的.实验所用的高光谱图像数据共包含100个波段,含有多种地物光谱.从图像中选择了玉米、灌木、干草3类地物的混合像元构成了混合像元矩阵.根据图像中的地物光谱信息生成了端元光谱库.OMP及其改进的稀疏解混算法对应得到的端元丰度RMSE值及平均丰度RMSE值如表2所示.

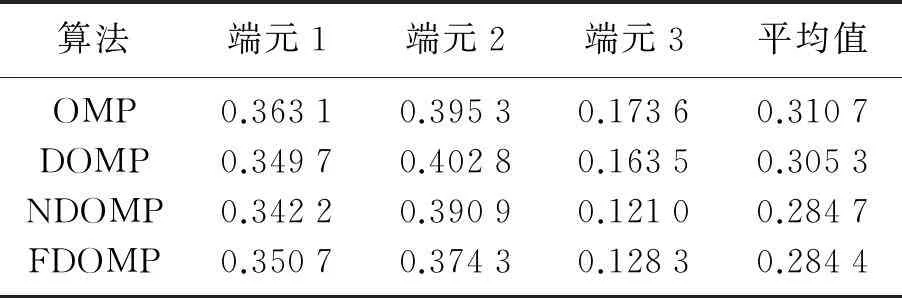
表2　稀疏解混算法的丰度RMSE值的对比

通过表2的真实高光谱图像的仿真实验结果可以看出,FDOMP改进算法明显地提高了稀疏解混的精确度,证明了该算法在高光谱数据实际应用中的有效性.改进算法在模拟数据和真实数据仿真实验中,都明显改善了解混效果,这也说明了DOMP算法与丰度全约束思想相结合的FDOMP算法在稀疏解混算法中具有实际应用价值.

图9是稀疏解混算法得到的端元3的丰度图对比.丰度值为1时,灰度图像上显示为白色.图9a中,白色区域是端元3丰度值为1的区域,通过观察对比图像,可以分析各稀疏解混算法反演丰度值完全正确的个数.从图9可以看到,FDOMP算法正确反演的个数相对较多,而OMP与DOMP算法丰度正确反演的个数相近,这也与RMSE的计算结果相符,再次验证了改进算法的有效性.

图9　端元3的丰度图对比

图10为实验所用真实高光谱数据混合像元的丰度误差,横轴表示丰度的RMSE值,纵轴表示混合像元的个数.RMSE值越小,说明混合像元反演得到的丰度越接近真实值.从图10中可以看到,FDOMP算法的RMSE值在0.1以下的像元个数更多,即正确反演的混合像元的个数更多.通过比较正确反演的像元个数,可以看到仍然是全约束DOMP算法的解混效果最好.图10从正确反演像元个数的角度验证了改进算法应用于稀疏解混的有效性.

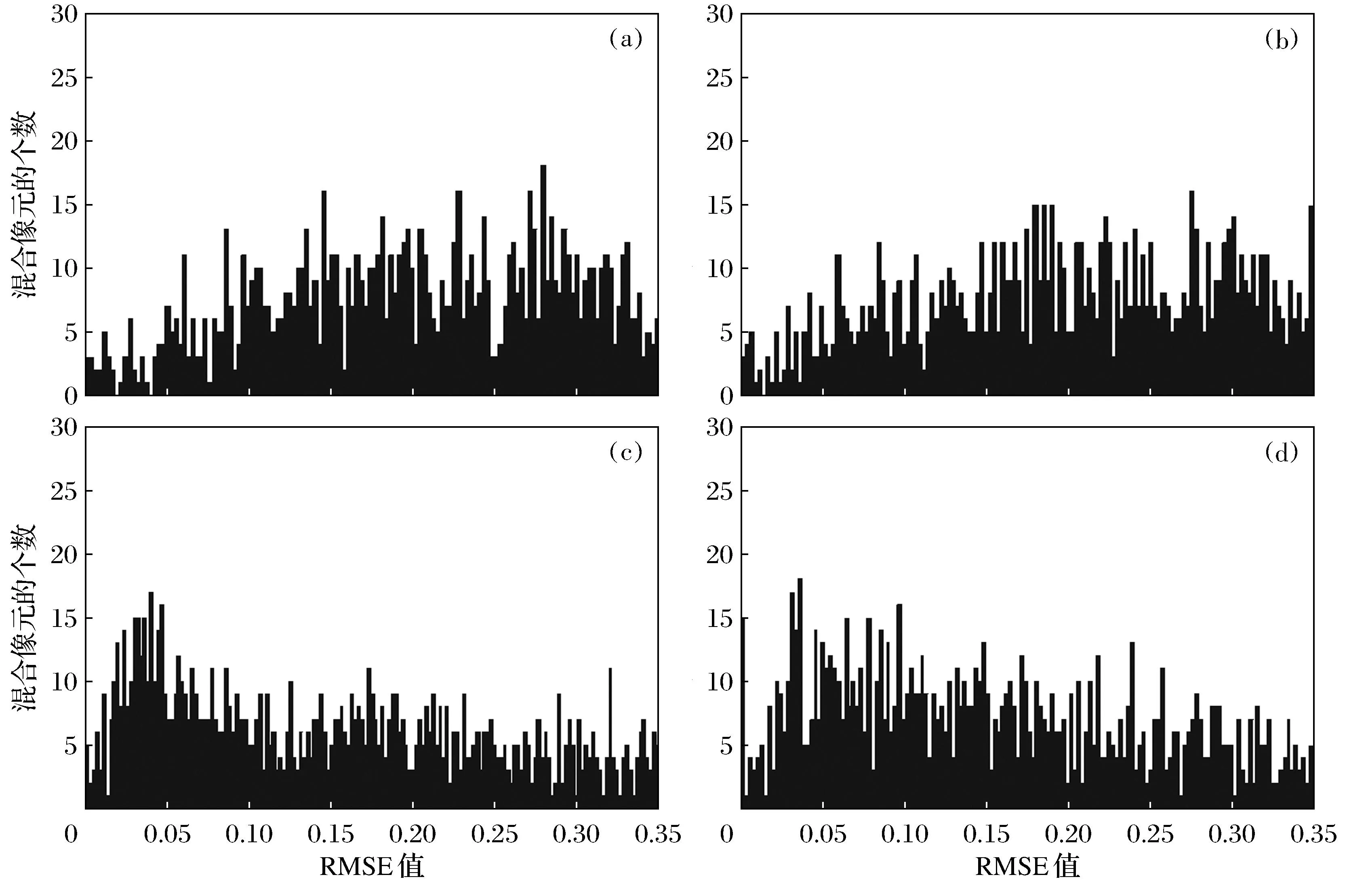
图10　真实数据像元的丰度RMSE

4　结　　语

在OMP稀疏解混算法的基础上,本文提出了全约束DOMP稀疏解混算法.采用Dice系数替代内积度量光谱匹配度,有效地减少了噪声对解混算法的影响.同时,在更新残差的计算过程中,引入了全约束最小二乘算法,使获得的丰度系数满足“非负”及“和为1”的性质,提高了稀疏解混算法的精确度.通过模拟和真实数据仿真实验,全约束DOMP算法的解混效果明显提升,验证了算法的有效性.但由于光谱库的选取对于稀疏解混的结果影响较大,因此,如何针对本算法更好地选择光谱库,使算法得到更好的应用,是今后研究的主要方向.

参考文献:

[1]王立国,赵春晖. 高光谱图像处理技术[M]. 北京:国防工业出版社, 2013:1-15.

(WangLiguo,ZhaoChunhui.ProcessingTechniquesofHyperspectralImagery[M].Beijing:NationalDefenseIndustryPress, 2013:1-15.)

[2]IordacheMD,DiasJB,PlazaA.UnmixingSparseHyperspectralMixtures[C]∥GeoscienceandRemoteSensingSymposium.CapeTown, 2009,4:85-88.

[3]IordacheMD,PlazaA,DiasJB.OntheUseofSpectralLibrariestoPerformSparseUnmixingofHyperspectralData[C]∥IEEEGRSSWorkshoponHyperspectralImageandSignalProcessing:EvolutioninRemoteSensing.Reykjavik:IEEEPress, 2010:1-4.

[4]DiasJB.AlternatingDirectionAlgorithmsforConstrainedSparseRegression:ApplicationtoHyperspectralUnmixing[C]∥The1stIEEEGRSSWorkshoponHyperspectralImageandSignalProcessing.Grenoble:IEEEPress, 2010:1-4.

[5]IordacheMD,DiasJB,PlazaA.TotalVariationSpatialRegularizationforSparseHyperspectralUnmixing[J].IEEETransactionsGeoscienceandRemoteSensing, 2012,50(11):4484-4502.

[6]IordacheMD,PlazaA,DiasJB.RecentDevelopmentsinSparseHyperspectralUnmixing[C]∥IEEEInternationalGeoscienceandRemoteSensingSymposium.Honolulu, 2010:1281-1284.

[7]ShiZW,TangW,DurenZ,etal.SubspaceMatchingPursuitforSparseUnmixingofHyperspectralData[J].IEEETransactionsonGeoscienceandRemoteSensing, 2014,52(6):3256-3274.

[8]IordacheMD,DiasJB,PlazaA.SparseUnmixingofHyperspectralData[J].IEEETransactionsGeoscienceandRemoteSensing, 2011,49(6):2014-2039.

[9]RaksuntornN,QianD,YounanN.OrthogonalMatchingPursuitforNonlinearUnmixingofHyperspectralImagery[C]∥The2ndIEEEChinaSummit&InternationalConferenceonSignalandInformationProcessing(ChinaSIP).Xi’an, 2014:157-161.

[10]张宇,刘雨东,计钊. 向量相似度测度方法[J]. 声学技术, 2009,28(4):532-536.

(ZhangYu,LiuYudong,JiZhao.VectorSimilarityMeasurementMethod[J].TechnicalAcoustics, 2009,28(4):532-536.)

[11]TangW,ShiZW,WuY.RegularizedSimultaneousForward-backwardGreedyAlgorithmforSparseUnmixingofHyperspectralData[J].IEEETransactionsGeoscienceandRemoteSensing, 2014,52(9):5271-5288.

[12]EhlerM,HirnM.SparseEndmemberExtractionandDemixing[C]∥GeoscienceandRemoteSensingSymposium.Munich, 2012:1385-1388.

[13]MohammadGA,ThomasSH.AFastOrthogonalMatchingPursuitAlgorithm[C]∥IEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing.Seattle,1998,3:1389-1392.

[14]AkhtarN,ShafaitF,MianA.FuturisticGreedyApproachtoSparseUnmixingofHyperspectralData[J].IEEETransactionsonGeoscienceandRemoteSensing, 2015,53(4):2157-2174.

[15]赵春晖,成宝芝,杨伟超. 利用约束非负矩阵分解的高光谱解混算法[J]. 哈尔滨工程大学学报, 2012,33(3):377-382.

【责任编辑:李艳】

(ZhaoChunhui,ChengBaozhi,YangWeichao.AlgorithmforHyperspectralUnmixingUsingConstrainedNonnegativeMatrixFactorization[J].JournalofHarbinEngineeringUniversity, 2012,33(3):377-382.)

AnImprovedOMPAlgorithmforHyperspectralSparseUnmixing

Zhao Chunhui, Xiao Jianyu, Qi Bin

(CollegeofInformationandCommunicationEngineering,HarbinEngineeringUniversity,Harbin150001,China)

Abstract:It will lead to undesirable unmixing results when OMP algorithm is used for noisy hyperspectral sparse unmixing. In order to solve this problem, a new constraint DOMP-based sparse unmixing algorithm is proposed, where the important spectral information could be highlighted by introducing Dice coefficient as the matching measurement criteria instead of inner product. Also considering constraints of abundance non-negativity and abundance sum-to-one, imposing “fully constraints” on the abundance values which improved the unmixing results. Experiments on both simulated and real hyperspectral data show that the proposed algorithms outperform the OMP sparse unmixing algorithm, the feasibility of the algorithms is proved.

Key words:hyperspectral imagery; sparse unmixing; orthogonal matching pursuit; generalized Dice coefficient; abundance constraints

作者简介:赵春晖(1965-),男,黑龙江汤原人,哈尔滨工程大学教授,博士生导师.

基金项目:国家自然科学基金资助项目(61405041);黑龙江省自然科学基金重点资助项目(ZD201216);哈尔滨市优秀学科带头人基金资助项目(RC2013XK009003);中国博士后科学基金资助项目(2014M551221).

收稿日期:2014-12-23

文章编号:2095-5456(2015)03-0206-08

中图分类号:TN911.2

文献标志码:A