关于双圈图的Harary指数*
邢抱花
(安庆师范学院 数学与计算科学学院,安徽 安庆246133)
1 预备知识
连通图G的Harary指数是一个很重要的拓扑参数,是在1993年由Plav¯sic′[1]等和Ivanciuc[2]等在刻划分子结构图时各自独立提出,且为了纪念Frank.Harary七十大寿而命名的.该拓扑指数被提出之后,许多学者对它进行了大量地研究,有关它的文章被陆续发表,部分结论可参见文献[4~8],其中文献[6]给出了n阶单圈图和n阶双圈图的Harary指数的上界以及相应的极图.本文主要研究双圈图去掉一条割边或添加一条边后其Harary指数的上界问题,并刻画了达到上界的极值图.
文中所涉及的图都是有限简单连通无向图,双圈图是具有n个点和n+1条边的连通图.设图G是一个简单连通图,V(G),E(G)分别是它的顶点集和边集,|V(G)|表示图G的阶,即顶点个数.图G的Harar y指数定义为图G中所有点对的距离的倒数之和,即

其中dG(u,v)是图G中顶点u,v之间的距离,即连接顶点u,v的最短路长度.在n阶星图Sn的两个悬挂点间添加一条边e后得到的新图,记为Sn+e.设e∈E(G),若图G-e的连通分支数大于图G连通分支数,则称e为G的一条割边.∀v∈V(G),v的距离是指图G中其余顶点到顶点v的距离之和,记为DG(v).文中没有被定义的其他术语和符号,读者可参见文献[3].
2 引理与主要结论

图1 连通图(n,3,3)与(n,3,3)
引理1[4]设G1,G2是连通图G的两个连通分支,V(G1)∩V(G2)={v},令G=G1v G2,则

引理2[5]设G是一个连通图,Tn和Sn分别是阶为n的一棵树和星图,V(H1)∩V(Tl)={}v,则

等号成立当且仅当Tn为Sn,其中在Gv Sn中v与星图Sn的中心粘合(等同).
引理3[6]设μ1(n)表示n阶单圈图的全体,G∈μ1(n),则等号成立当且仅当G为Sn+e.
引理4[6]设μ2(n)表示n阶双圈图的全体,G∈μ2(n),则等号成立当且仅当G为(n,3,3)或G为(n,3,3).(n,3,3)(n,3,3)见图1)
证明:设双圈图G=G1v G2,其中V(G1)∩V(G2)={v},且G1,G2分别是s,t阶单圈图,s+t=n+1,则由引理1和引理3,得:

等号成立当且仅当G1为s阶星图,G2为t阶星图,且v是G1与G2的中心,即等号成立当且仅当G=(n,3,3).经计算故结论成立.
定理1 设G∈μ2(n),G*表示G-e,其中e为割边,则

等式成立当且仅当G*是由两个连通分支S n2+e和S n2+e所构成的图或G*是由两个连通分支和所构成的图或G*是由两个连通分支和所构成的图.
证明:∀G∈μ2(n),图G*=G-e的两个连通分支的情况可能是:1)一个双圈图G1和一棵树T1;2)两个单圈图G2,G3.
对于情况(1),设V(T1)=x,V(G1)=n-x,则由引理2和4得:

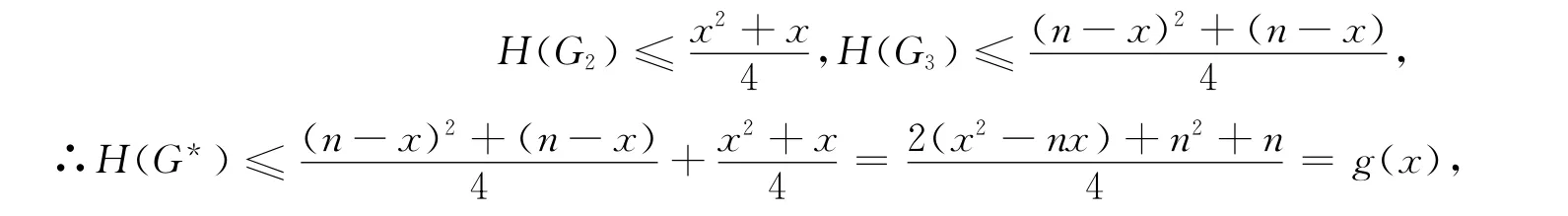
定理2 设G∈μ2(n),G**表示在图G中添加一条边e后得到的新图,e∉E(G),则等号成立当且仅当G**是星图Sn添加两条边后得到的图.

证明:由题意知,图G**是n阶三圈图,可以把它看成是一个n1阶单圈图G1与一个n2阶双圈图G2的粘图,即G**=G1v G2,V(G1)∩V(G2)={v},且n1+n2=n+1.
由引理3和引理4得,

等号成立当且仅当G1为Sn1+e;G2为(n2,3,3)或G2为G*2(n2,3,3).
等号成立当且仅当在图G1中,v是图G1=Sn1+e中度最大的顶点,在图G2中,v是图G2=(n2,3,3)中度最大的顶点或v是图G2=(n2,3,3)中度最大的顶点.故

等号成立当且仅当G**=(Sn1+e)v(n2,3,3))或G**=(Sn1+e)v(n2,3,3)),且此时顶点v是图G1=Sn1+e中度最大的顶点,同时,顶点v又是图G2=(n2,3,3)中度最大的顶点或图G2=(n2,3,3)中度最大的顶点,故三圈图G**可看成星图Sn添加两条边后得到的图.
[1]Plavi D,Nikoli S,Trinajstin,etal.On t he Harar y index f or the characterization of chemical graphs[J].Math Chem,1993,12:235-250.
[2]Ivanciuc O,Balaban S T,Balaban T A.Reciprocal diatance matrix,related local vertex invariants and topological indices[J].Math Chem,1993,12:309-318.
[3]Bondy A,Mmurty U S R.Graph Theory with Application[M].New York:Mac millan Press,1976.
[4]K.Xu,N.Trinajstic.Hyper-Wiener and Harary indices of graphs with cut edges[J].Util.Math.,2011,84:153-163.
[5]K.Xu.Trees wit h the seven s mallest and eight greatest Harar y indices[J].Discrete Applied Mathematics,2012,160(3):321-331.
[6]K.Xu,K.C.Das.Extremal Unicyclic and Bicyclic Graphs with Respect to Harary Index[J].Bull.Malays.Math.Sci.Soc(2),2013,36(2):373-383.
[7]李小新,査淑萍,范益政.连通图的Harary指数上界及其极图[J].中国科学技术大学学报,2014,44(2):96-100.
[8]肖金环,赵飚.固定直径的树的Harary指数[J].曲阜师范大学学报(自然科学版),2014,40(3):30-34.

