基于S7-200 PLC自整定PID控制系统的设计与仿真

王 超李 斌

（1,2.昌吉学院物理系 新疆 昌吉 831100）

引言

工业生产中，一般采用闭环控制方式来控制温度、压力、流量等连续变化的模拟量，使用最多的就是PID控制，PID控制器结构典型，程序设计简单，各个参数具有明确的物理意义，比较容易实现多回路、串级等复杂控制[1-2]。但是，如果仅仅依靠常规的PID来实现，控制系统的“稳、快、准”要求难以实现。将PID与自整定算法结合起来，使得PID控制具有了更为强大的生命力，控制系统的性能指标也较为容易达到要求。

1 PID控制器参数自整定原理

1.1 PID控制器

典型PID模拟量控制系统如图1所示，SP（t）为设定值，PV（t）为过程变量，C（t）为被控量，M（t）为PID输出量，PID调节器的输入输出关系为[3]：

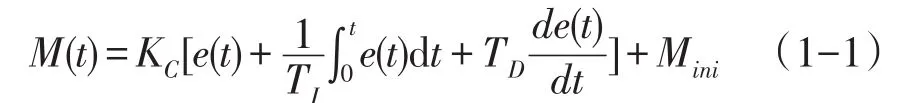
连续的PID运算需要数字化后才能在S7-200PLC中进行处理，式（1-1）中的积分项用矩形法数值积分代替，微分用一阶后向差分近似代替，得到第n次采样时控制器的输出为[4]：

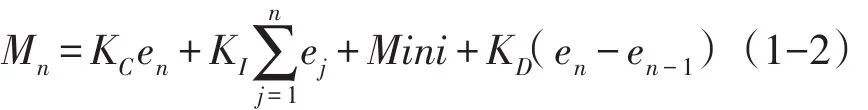
在用PID编写程序时，需要把过程变量PV转换为0.0—1.0之间的标准化数值，PID运算完成后，需要把回路输出转换为整数，直接用PID指令编程繁杂，用编程软件中随带的PID指令向导可以减少编写PID控制程序的难度，非常便于使用。

1.2 PID控制器自整定原理

S7-200使用的自整定算法是基于继电反馈算法，可以用于正作用和反作用的P、PI、PD、PID回路的自整定，它用继电特性的非线性环节代替ZN法中的纯比例控制器，使系统出现极限环，从而获取所需要的临界值。其基本思想是在控制系统中设置两种模态：测试模态和调节模态，在测试模态下，由一个继电非线性环节来测试系统的振荡频率和增益，在调节模态下，有系统的特征参数首先得到PID控制器，然后由此控制器对系统的动态性能进行调节，如果系统的参数发生变化，则需要重新进入测试模态进行测试，测试完毕后再回到调节模态进行控制[3]。

2 S7-200PLC的PID参数自整定调试

2.1 被控对象建立

被控对象的数学模型由式（1-3）式确定[5]，由三个串联的惯性环节，时间常数分别为TIM1—TIM3，GAIN为增益，可以根据需要将某一个时间常数设置为0。

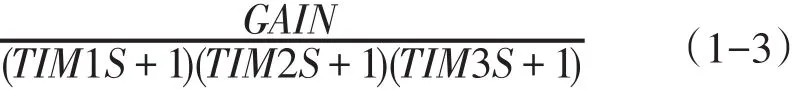
在STEP7-Micro/Win编程软件中，用软件完成被控对象的模拟，如图2所示，其中GAIN=3.0，TIM1=5000，TIM2=2000，TIM3=0，构建的被控对象数学模型为：

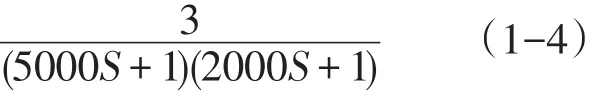
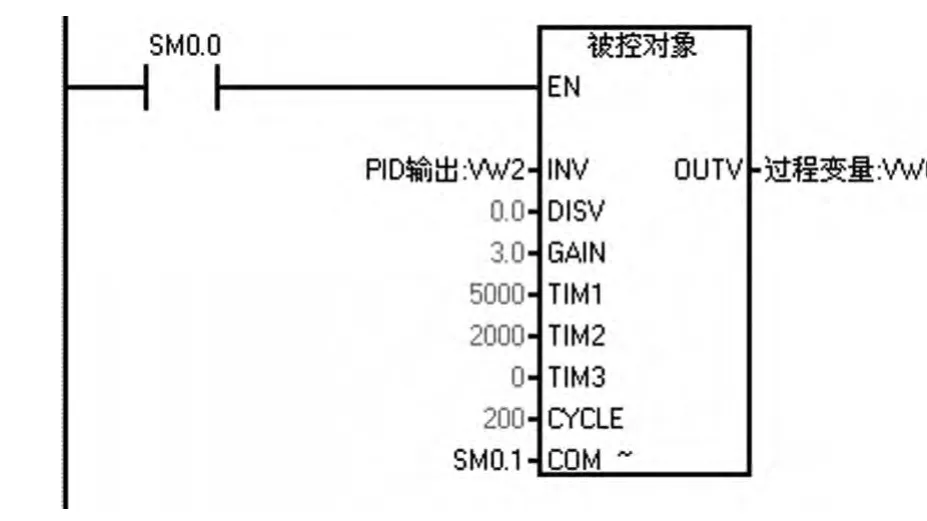
图2 被控对象模拟

2.2 PID向导建立PID指令

在STEP7-Micro/Win编程软件中可以使用PID向导自动生成子程序PID_INI和PID_EXE，PID_INI用于初始化PID控制的变量，CPU按照PID向导中组态的采样周期调用PID中断程序PID_EXE，在PID_EXE中执行PID运算，PID程序如图3所示，PV_I是过程变量（反馈值），Setpoint_R为给定值，Auto_Manual为手动/自动模式切换，ManualOutput是手动模式时标准化的实数输入值，Output是PID控制器的输出值，High Alarm是上限报警，可以根据需要在向导生成过程中选择，当I0.0由0变为1时，由手动方式调整为自动方式。

图3 PID指令

2.3 PID控制系统调试

在STEP7-Micro/Win编程软件下，单击工具PID调节面板，既可以打开PID调节面板，如图4所示，该调节面板主要由以下几部分组成：过程变量、当前值区、图形显示区、调节参数区等。用户通过图形显示区观察输出曲线的变化，输出的曲线用不同颜色分别表示过程量、给定值和输出值。PID参数自整定之前，控制过程应该处于稳定状态，过程变量接近设定值，并且输出没有不规律的变化，开始自整定时，理想的情况是回路输出值在控制范围的中点附近，可以通过手动调节使控制过程接近稳定。

图4 PID调节面板

2.3.1 确定比例增益KC

首先去掉PID积分项和微分项，即积分时间为INF，微分时间为0，不断修改KC的值（由0增加到15），直至出现振荡。之后，在逐渐减小KC直至看不出振荡，记下此时的KC值为5，但仍然存在稳态误差，如图5所示。

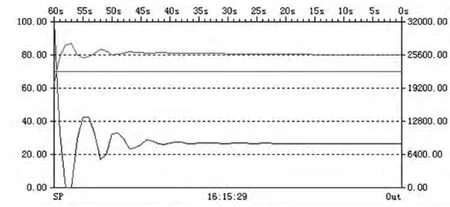
图5 KC=5阶跃曲线

2.3.2 确定积分时间常数Ti

在比例增益KC确定后，在此基础上引入一个较强的积分环节，因积分常数与时间成反比，先设置Ti=0.01，Td=0，让系统产生振荡，之后在逐渐增大积分时间常数Ti，使系统不产生振荡，此时可以记下参数Ti的数值为0.1，过程变量逐渐靠近给定值SP，这说明积分的作用可以消除稳态误差，提高系统的控制精度，如图6所示。

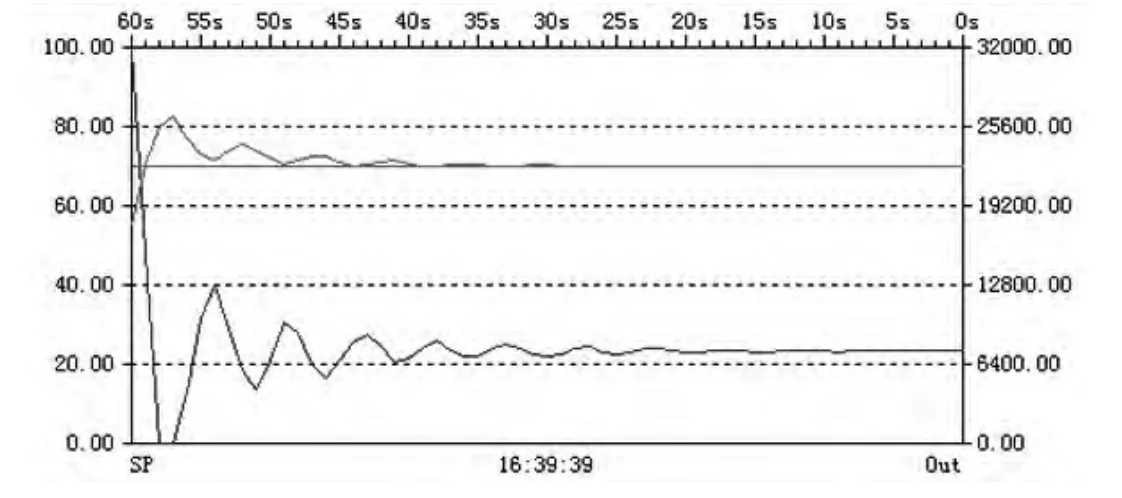
图6 KC=5，Ti=0.1阶跃曲线

2.3.3 确定微分时间常数Td

微分部分具有超前调节和预测误差的作用，增大Td可以改善系统动态性能、减小超调量，但是抑制高频干扰能力降低。整定时，可以先设置较大的Td，让系统产生振荡，之后逐渐减小，记下临界时的Td值，如图7所示，此时Td为0.008。

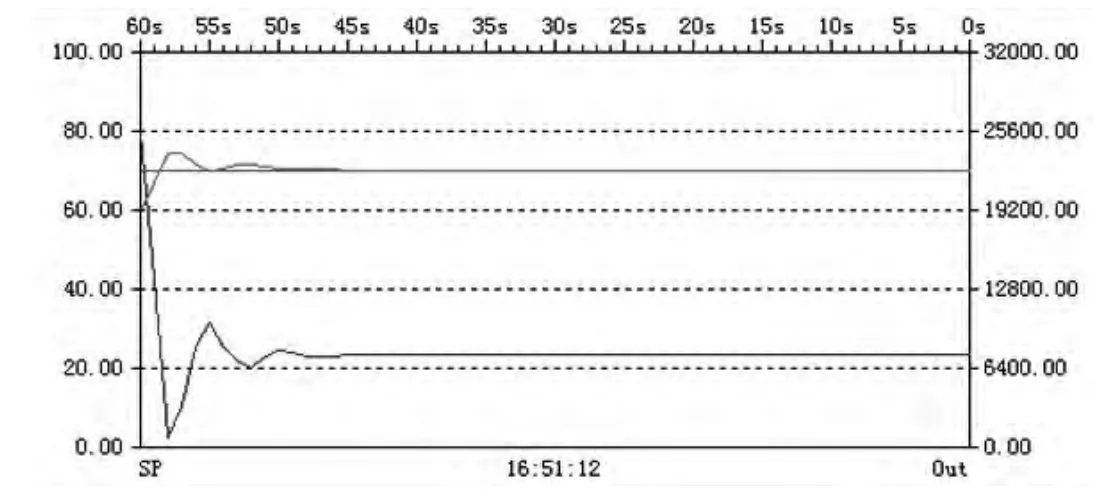
图7 KC=5，Ti=0.1,Td=0.008阶跃曲线

2.3.4 PID参数自整定

在系统稳定输出后，单击“开始自动调节”按钮，系统启动参数自整定过程，面板右下部分的区域显示“PLC正在计算滞后死区值和偏差”，滞后计算结束后，显示“PLC正在调节PID0”，PID的输出按照方波变化，PV的波形沿着SP水平线上下波动，如图8所示。

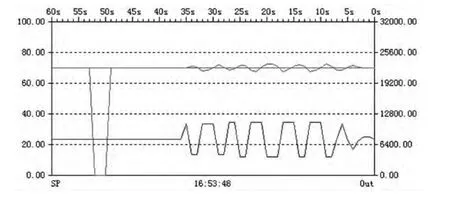
图8 PID自整定调节PID0曲线

显示“调节算法正常完成，算法建议的调节参数已经可用”时，进入正常的PID控制，PID输出的波形由方波变为平滑曲线，PV的波形逐渐趋于设定值SP，如图9所示，“调节参数区”给出了PID参数的建议值。

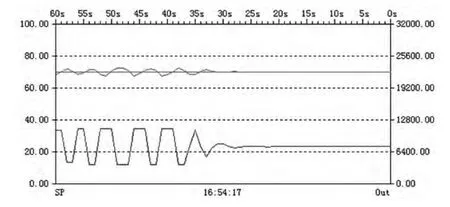
图9 PID自整定调节算法完成曲线

单击“更新PLC”按钮，既可以将自整定得到的推荐参数写到CPU中，KC=3.401，Ti=0.0433，Td=0.0158，如图10所示。动态指标很好地满足了要求，即PID自整定算法推荐了接近最优的增益、积分时间和微分时间。

图10 PID自整定曲线

3 结论

将S7-200自整定PID引入到闭环控制系统中，借助PID调节控制面板，采用手动调节和PID算法自整定功能相结合，使用户能够轻松地实现PID的参数自整定，可以获得接近最优的增益、积分时间和微分时间，对实际工程PID参数整定具有一定的参考价值。

［1］廖常初.PLC编程及应用［M］.北京：机械工业出版社，2015.

［2］刘金琨.先进PIK控制MATLAB仿真（第3版）［M］.北京电子工业出版社，2012.

［3］曾喜娟，庄其仁.基于S7-200PLC的PID参数自整定法［J］.控制与检测，2010，(1):47-50.

［4］穆帅欢，王洪诚.基于S7-200的液位PID控制系统设计［J］.自动化应用，2014，（2）：50-52.

［5］杨津听，熊浩.S7-200PLCde PID自整定算法剖析［J］.工业控制计算机,2012,25(5):9-11.