圆锥曲线一般方程化最简方程的系数公式——公式法化简圆锥曲线一般方程

雷崇耀

（昌吉学院 新疆 昌吉 831100）

16世纪法国人韦达在初等数学的教学中，发现了一元二次方程的根和系数间的关系，今天被人们称做韦达定理，成为法兰西民族对人类文明的一大贡献。在二元二次方程的教学中，我们发现了圆锥曲线一般方程与最简方程系数间的关系，推导出了圆锥曲线一般方程化最简方程的一整套公式。

定理：设圆锥曲线的一般方程为Ax2+Bxy+Cy2+Dx+Ey+F=0，令

Δ1叫做曲线态的判别式，Δ2叫做曲线型的判别式，则我们有如下结论：

（1）当Δ1=0时为变态曲线，即曲线退缩为直线或点，或无轨迹。

（2）当Δ2≠0时为有心曲线。先用坐标平移变换消去一次项。后用坐标旋转变换消去交叉项。曲线可化为最简方程：

其系数公式为：

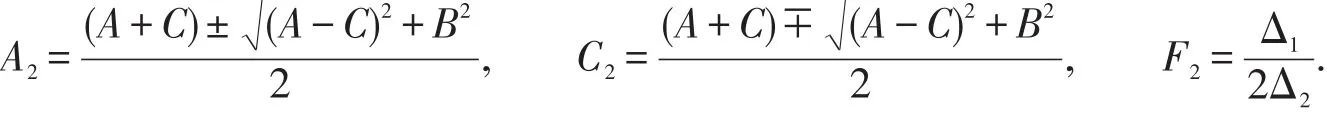
（3）当Δ2=0时为无心曲线。先用坐标旋转变换消去交叉项，后用坐标平移变换消去适当项，曲线可化为最简方程：

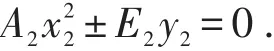
其系数公式为：

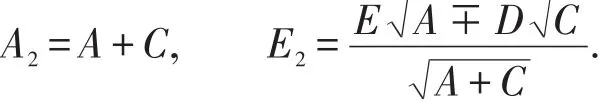
以上公式中，B≥0时取上符号，B〈0时取下符号。证明

第一步先用坐标平移变换消去方程中一次项。

把移轴公式x=x1+x0，y=y1+y0代入方程：

展开后合并同类项，得

令（2）中两个一次项系数为0，解方程组：

求得新原点的坐标：

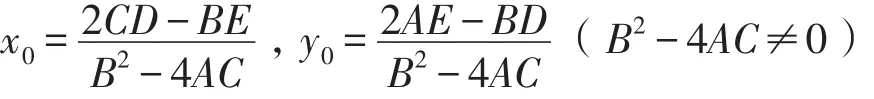
将新原点的坐标值代入（2），得

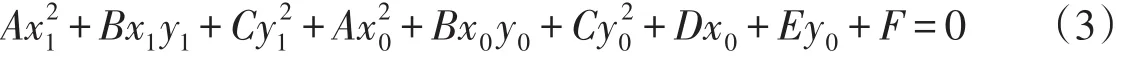
经坐标平移后方程中各项系数依次为：A1=A,B1=B,C1=C,D1=E1=0,常数项:

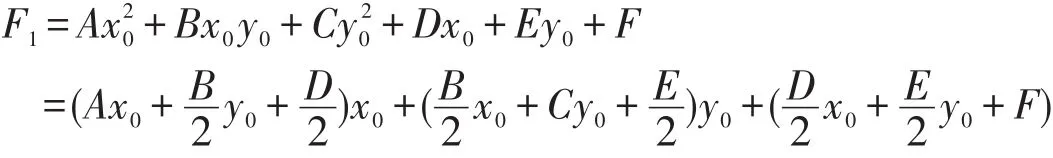
因为x0,y0的值满足前方程组，所以

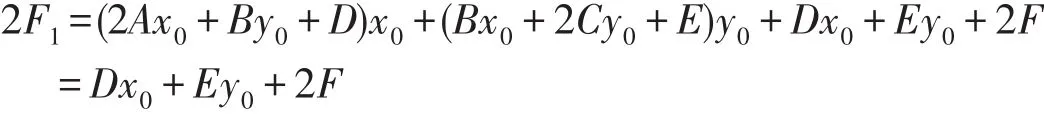
故（3）中常数项

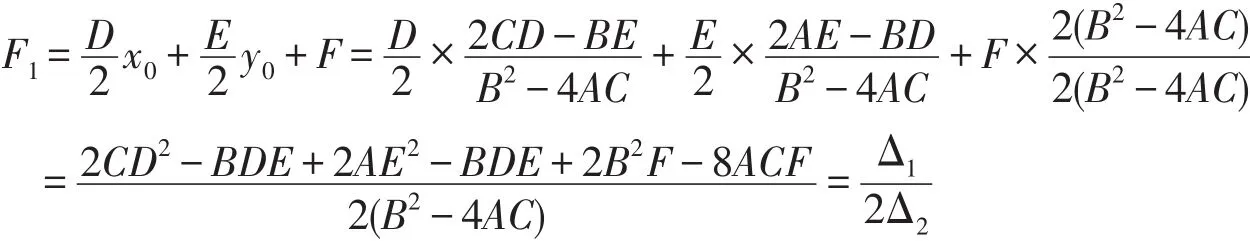
经过坐标平移后方程（1）化为：

第二步后用坐标旋转变换消去方程（4）中交叉项x1y1。

把转轴公式 x1=x2cosα-y2sinα和 y1=x2sinα+y2cosα代入（4）中，得

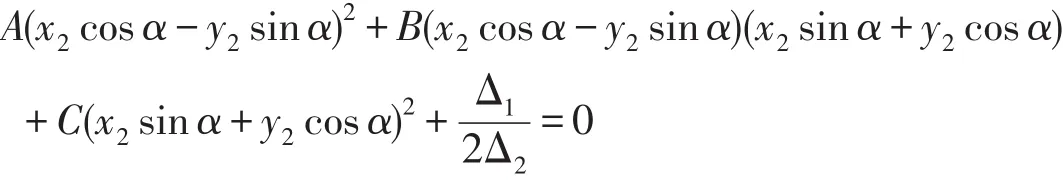
展开，合并同类项，可得下列形式的方程：

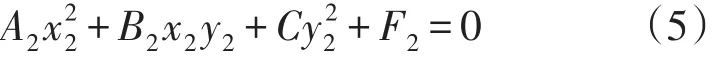
其中，各项系数依次为：

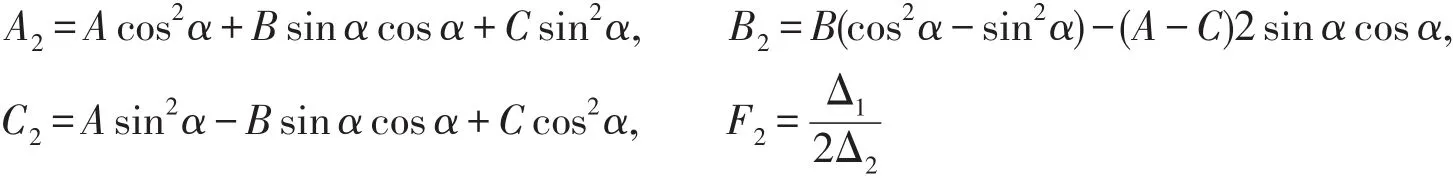
为了确定α使得交叉项x2y2消失，令B2=0，即令

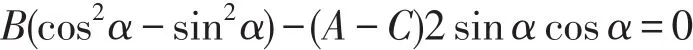
根据三角公式cos2α-sin2α=cos2α和2sinαcosα=sin2α，可得

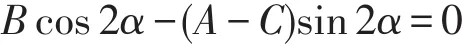
从而求得

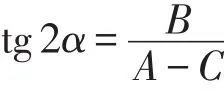
再利用三角公式

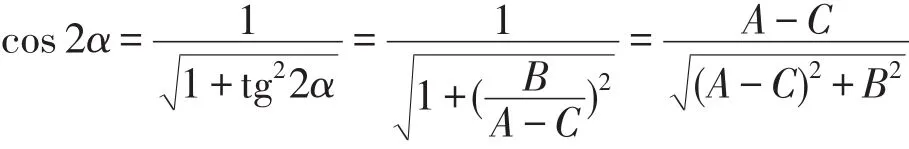
从而求得

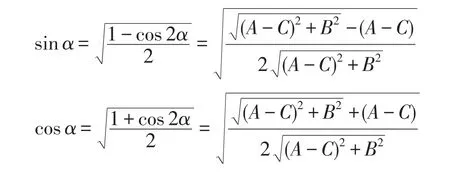
先用坐标平移变换，后用坐标旋转变换后（5）式化为最简方程：

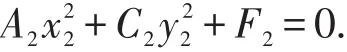
其系数公式为:

公式(1)中B≥0时取上符号，B〈0时取下符号。

结论

第一步先用坐标旋转变换消去交叉项。

把转轴公式x=x1cosα-y1sinα和y=x1sinα+y1cosα代入方程

展开后合并同类项，可得下列形式的方程：

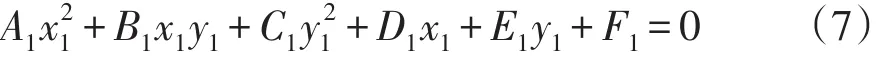
方程中各项系数依次为：

为了确定α使得交叉项x1y1消失，令B1=0，即令

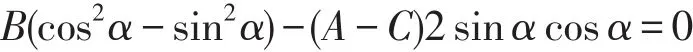
根据三角公式cos2α-sin2α=cos2α和2sinαcosα=sin2α，可得B cos2α-(A-C)sin2α=0

从而求得

再利用三角公式

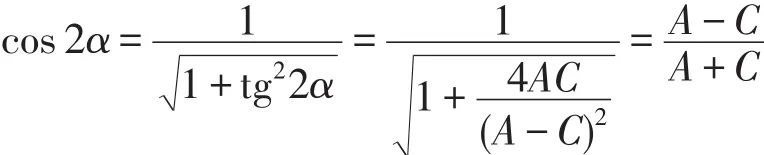
从而求得

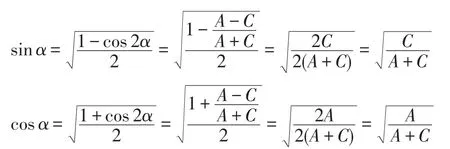
将求得的sinα和cosα的值代入（7），得到各系数为：

经过坐标旋转变换后方程化为：

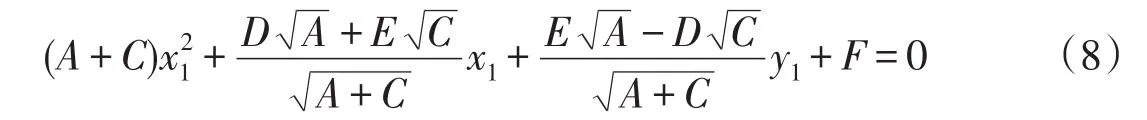
第二步后用坐标平移变换消去适当项。

将移轴公式 x1=x2+x0和 y1=y2+y0代入（8），得

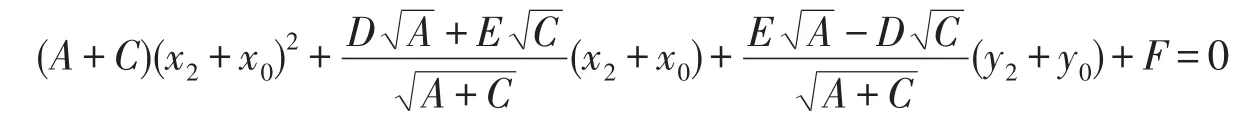
展开后合并同类项，可得下列形式的方程：

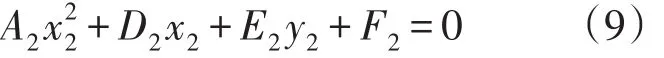
方程中各项系数为：

为了求出新坐标系的原点坐标，令一次项x2的系数D2和常数项F2为0，解方程组：

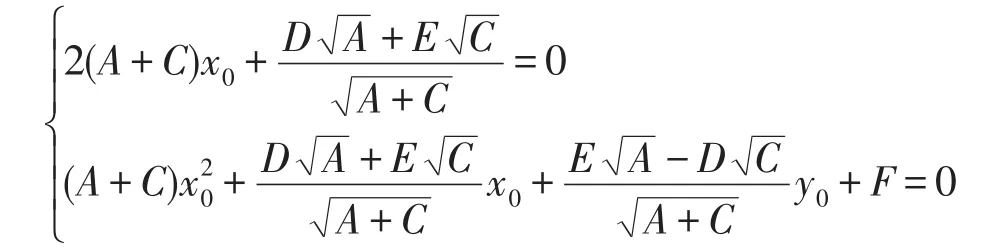
求得新原点的坐标为：

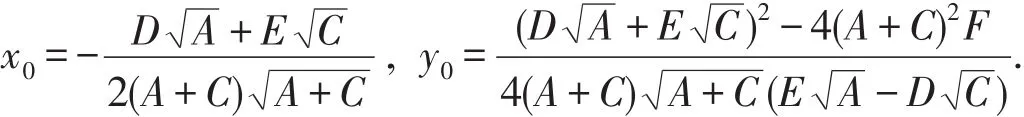
将新原点的坐标值代入（9）式，可化为最简方程：

其系数公式为:

方程中B≥0时取上符号，B〈0时取下符号。

［1］樊咉川等编.高等数学讲义［M］.北京:高等教育出版社，1965.

［2］吴光磊,丁石孙,姜伯驹,田畴等编.解析几何［M］.北京:人民教育出版社，1978.