非等温粘弹性流体充模的SPH方法建模探究
摘 要:充模过程是注塑成型过程中最复杂最重要的阶段。目前充模过程的大部分数值模拟研究都是基于网格类方法,而网格类方法在处理复杂自由面时存在一定的困难。因此,该文对无网格SPH方法在非等温聚合物充模问题中的应用进行了试探性研究。首先阐述了SPH方法在非等温流动模拟方面的发展现状及其存在的问题,然后以粘弹性XPP流体为例,建立了非等温聚合物充模问题的SPH离散模型,最后通过基准算例验证了所建立的非等温粘弹性模型的有效性和准确性。
关键词:光滑粒子动力学(SPH)方法 非等温 粘弹性流体 充模过程
中图分类号:O35 文献标识码:A 文章编号:1674-098X(2015)09(c)-0007-02
1 非等温流动的SPH方法研究现状
众所周知,充模过程是注塑成型过程中最复杂最重要的阶段。此过程一般要求熔体快速充满模腔,不可避免地形成了喷流痕、气穴、填充不足等诸多注塑成型缺陷。这些缺陷严重影响了塑料制品的表面质量、光学性能和力学性能。然而充模过程中模腔始终保持封闭状态,人们难以观察到熔体在模腔内的流动情况。因此,数值模拟技术成为一种有效预测充模过程的强有力手段。
目前已发展了多种数值方法[1]研究充模过程,如有限差分法(FDM)、有限体积法(FVM)、有限元方法(FEM)等。然而,上述方法都是基于网格的方法,在处理复杂自由面流动问题时存在一些困难,如FDM、FVM均是基于Euler描述的网格类方法,不能直接追踪自由表面、运动物质交界面等,需要引入额外的界面捕捉技术(如MAC方法、VOF方法、Level Set方法等),FEM模拟大变形问题时容易出现网格扭曲、程序实施较复杂等。与有限元类似的数值方法是边界元方法(Boundary Element Method, BEM),BEM在计算过程中需要不断进行网格重构。此外,上述方法中网格生成是一项十分耗时的工作,对于复杂形体的网格划分十分困难,求解过程中常出现网格畸变严重的情况,从而导致求解精度低甚至发散。因此,人们发展了无网格方法来研究具有复杂自由面的流动问题。
光滑粒子流体动力学(Smoothed Particle Hydrodynamics)方法[2]是一种基于Lagrange描述的无网格粒子法,此方法在计算中不需要网格,避免了大变形问题中网格重构、网格畸变等问题,其计算精度不受结构变形程度的影响。由于SPH方法的纯Lagrange特性及粒子特性,可以通过粒子本身的位置自动追踪运动界面,SPH方法自提出后受到了众多研究者的广泛关注,并广泛应用于计算流体力学各个领域。然而,SPH方法却很少应用于非等温粘弹性流体充模过程的流动模拟方面。一方面,粘弹性流体控制方程的非线性性质远强于牛顿流体,其数值模拟对数值格式的要求远高于牛顿流体。目前已有的SPH离散格式不适合这类聚合物充模过程的模拟。若要得到比较稳定的SPH解,只能选择非常小的时间步长,计算效率太低。因此,传统SPH方法被认为不适合模拟聚合物充模过程。为了提高传统SPH方法的数值精度和数值稳定性,人们提出了多种改进SPH方法[3],如RKPM、CSPM、MSPH,SSPH,FPM等。然而这些改进方法提高了传统SPH方法的数值精度和稳定性的同时,也引入了其它问题,如实施过程繁琐、计算量大、局部矩阵容易发生奇异等,不易推广应用,从而未被广泛应用于流体力学领域。另一方面,聚合物充模过程是一个非等温过程,具有对流扩散性质的温度方程的离散方式及求解对充填结果有很大影响,而目前关于非等温粘弹性流体流动模拟的SPH离散模型还未建立。
基于上述原因,该文针对非等温粘弹性流体充模问题,试探性地建立非等温粘弹性流体充模问题的改进SPH离散模型。首先阐述非等温粘弹性流体流动的控制方程,然后对控制方程尤其是温度控制方程进行SPH离散,从而建立非等温粘弹性流体充模过程的SPH离散模型。最后通过简单的数值算例验证了所建立模型的收敛性、有效性。
2 非等温粘弹性流体充模过程的SPH离散模型的建立
二维情况下,流体控制方程为
(1)
(2)
其中為外力,包括重力及约束力等。为应力张量,当熔体为非等温非牛顿粘性流体时,。当熔体为粘弹性流体时,,其中为各向异性压力,为非牛顿聚合物溶剂贡献的偏应力。该文考虑非等温粘弹性XPP流体的简化模型Oldroyd-B模型的充模过程,XPP本构模型的表达式为
(3)
其中为单位张量,形变率张量,,
,为速度梯度张量,为速度梯度张量的转置。、分别表示聚合物分子链的取向和拉伸松弛时间,为线性松弛模量,为各向异性无关的参数,拉伸量,。总粘度,其中,,。当和时,XPP模型退化为Oldroyd-B模型。
温度控制方程为
(4)
其中是熔体温度,、和分别表示熔体的密度、比热容和导热系数。熔体粘度与温度的关系用下列热幂律模型来描述[3]。
为了能够对聚合物充模过程进行数值模拟,下面对流体控制方程进行SPH离散。密度的求解仍采用连续性方程
(5)
而对于动量方程离散,该文推广文献[2]中非牛顿粘性流体的动量离散形式,考虑弹性的影响,从而有
(6)
其中。
对于粘弹性本构方程,则采取如下的离散方式
,
(7)
(8)
对于温度控制方程(4)的SPH离散,作者及其合作者在参考文献[2]中针对非等温粘性流体充模过程提出了非牛顿粘性熔体的改进SPH温度离散模型,即
(9)
其中,,,为修正核梯度。
可以看出,式(9)未考虑聚合物熔体的弹性对熔体流动和温度的影响。于是,推广上面非牛顿粘性流体的SPH温度离散模型(9),考虑熔体弹性对流体的流动和温度的影响,则得到如下的粘弹性流体的改进SPH温度离散模型
(10)
其中,,。
式(5)~(8)和式(10)构成了非等温粘弹性熔体充模过程的SPH离散模型。
3 数值验证
为了验证所建立的非等温粘弹性流体充模过程的SPH离散模型的有效性,本小节模拟非等温粘弹性Oldroyd-B流体的Poiseuille流。采用的参数为:密度为 ,熔体初始粘度 ,壁面温度 ,熔体温度 ,温度依赖参数,比热容 ,导热系数 ,,,,幂律指数,力 ,时间步长 。
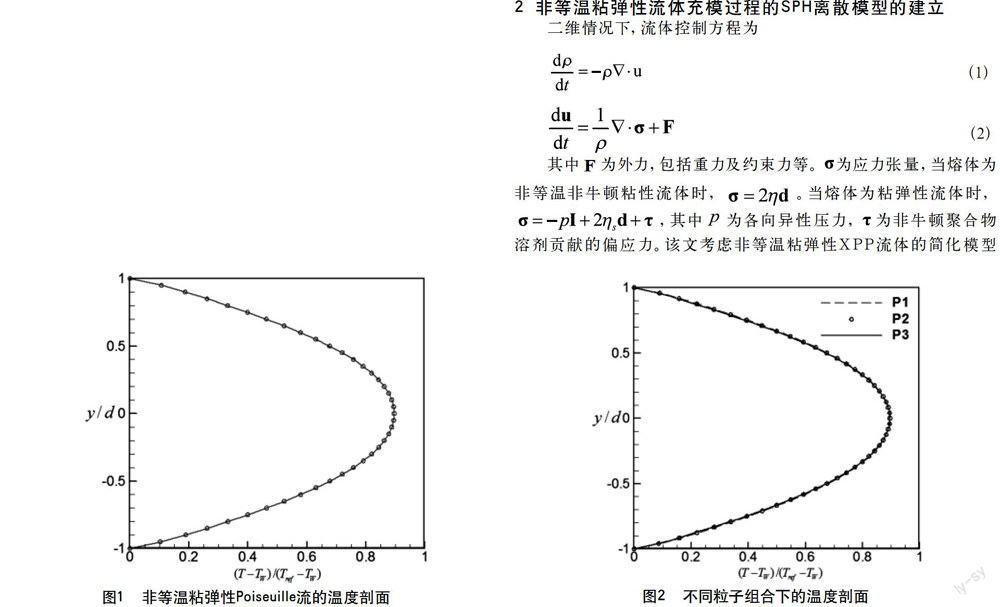
图1给出了非等温粘弹性Poiseuille流在速度达到稳态时的温度剖面。可以看出,所得温度剖面呈抛物形,与文献[4]中给出的温度的变化趋势类似,这说明给出的粘弹性温度离散模型是有效的。由于该文与文献[4]中所采用的本构方程、参数等条件不同会造成温度值的差异,所以这里仅做定性比较。
图2给出了3种不同粒子数下的温度剖面。采用的3种粒子组合分别为P1:P2:和P3:。由图2可以看出,三种不同粒子数下得到的温度剖面变化趋势一致,说明给出的粘弹性SPH温度离散模型收敛。
图1与图2的数值结果表明,该文建立的非等温粘弹性流动的SPH离散模型是收敛、有效的。
4 结语
该文首先对SPH方法应用于非等温聚合物流动问题的研究现状进行了阐述,分析了SPH方法很少用于非等溫聚合物充模问题的原因,然后根据相关文献及作者的数值模拟经验建立了非等温粘弹性流体充模过程的SPH离散模型,最后通过非等温粘弹性Poiseuille流数值算例的模拟,验证了所建立的非等温粘弹性流体的SPH离散模型的有效性和收敛性。
值得注意的是,该文没有对非等温粘弹性流体充模问题进行数值模拟和分析,后续作者将对此问题进行研究讨论。
参考文献
[1] JinlianRen,JieOuyang,Tao Jiang.Simulation of complex filling process based on the generalized Newtonian fluid model using a corrected SPH scheme[J].Computational Mechanics,2012,49:643-665.
[2] 蒋涛,任金莲,徐磊,等.非等温非牛顿黏性流体流动问题的修正光滑粒子动力学方法模拟[J].物理学报,2014,63(21):22-34.
[3] 任金莲.SPH方法改进及其在聚合物充模问题中的应用研究[D].西安:西北工业大学,2014.
[4] A.Ahsan.Evaporation,Condensation and Heat transfer,Croatia:InTech,2011.