无线传感器网络中APIT—HR定位算法*

周礼争，张乙竹，唐 瑞，余 敏

(1.江西师范大学计算机信息工程学院，江西南昌330022;2.江西师范大学软件学院，江西南昌330022)

0 引言

节点定位技术一直是学术界研究的重点。在室外，一般有基于全球定位系统(GPS)定位技术、基于移动蜂窝网络定位技术、基于无线传感器网络(wireless sensor networks，WSNs)定位技术［1］。在室内，一般有基于接收信号强度指示(received signal strength indication，RSSI)定位技术、航位推算定位技术［2］。然而，WSNs因其具有随机部署、网络自组织、覆盖范围广等优点，故其应用非常广泛，如生态农业检测、智能安防、现代信息化作战等。

WSNs节点定位方法分为基于测距(range-based)和基于非测距(ranged-free)两类［3，4］。基于测距的方法需测量彼此间的绝对距离或角度，再用相关方法估算节点位置信息［5，6］，如 TOA，TDOA 等。基于非测距的测量法是以节点间连通性、相邻特性求解节点位置信息，如质心法、近似四面体内点(approximate point-in-tetrahedron，APIT)、凸规划法等［7，8］。基于测距的定位技术定位精度较高，但对WSNs节点的硬件要求较高，因此，在WSNs的现发展阶段性价比不算高。而基于非测距的定位算法定位精度虽然不理想，但能够满足大多数应用的定位需求。APIT算法相对其他基于非测距定位算法，在定位精度、硬件成本、节点分布等方面性能较好。

文献［7］提出基于RSSI的加权质心定位算法，定位精度有所提高。文献［8］提出基于三角形角度的加权质心算法，能较好地改善定位精度。文献［9］提出基于区域的非测距APIT定位算法，但算法通信开销大、定位精度低。文献［10］提出基于垂直平分线的区域定位算法，文献［11］提出改进的APIT(IAPIT)定位算法均力图提高定位精度。

在上述文献基础上，本文提出基于RSSI值折半的APIT(APIT—HR)质心定位算法，以RSSI值比较进行区域约束划分，以节点存在区域质心作为定位结果。

1 相关算法描述

1.1 RSSI损耗模型

无线信号传播较为常用的模型是Shadowing模型，该模型参考式为

其中，RSSId为接收到的信号强度值;d为收发端的实际距离;d0为参考距离;RSSId0为距离为d0时的信号强度;n为信道衰减指数，由传输环境决定;Xσ是方差为σ、均值为0的高斯随机变量。由式(1)变形可得d与RSSId之间一阶导数和二阶导数关系

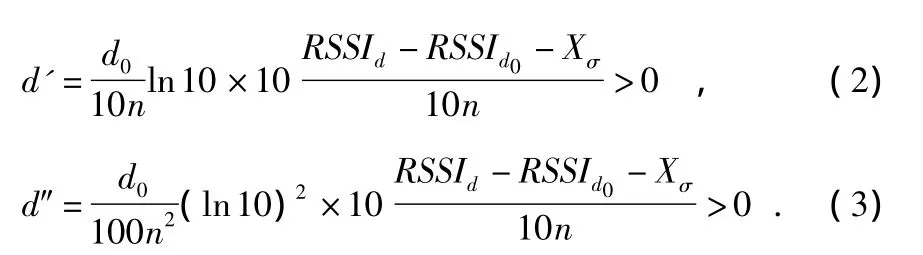
由式(1)～式(3)可知，若RSSI1值对应的距离d1时，则值对应的距离

1.2 APIT算法分析

该算法的核心思想:任取3个锚节点组成三角形，再以某种方法［10］判断未知节点是否在该三角形内部，若在，则称三角形约束区域包含未知节点。以此类推，求所有符合要求的三角形约束区域交集的质心作为未知节点近似坐标。APIT算法的基础是PIT测试定理［10］。PIT测试中，通常以RSSI的强弱来判断远离或靠近锚节点。

APIT算法存在以下缺陷:

1)在判断未知节点是否在三角形区域内部时，易产生InToOut和OutToIn错误。如图1(a)，当节点M从位置1模拟移动到位置2时，收到来自A，B，C的信号强度同时变弱，节点M同时远离A，B，C点，就判定为M在三角形外，即In-ToOut error。同理，图1(b)，当节点M从位置1模拟移动到位置2时，根据信号强度测得节点M就远离了B，并靠近了A，C点，就判定为M在三角形内，即OutToIn error。

2)在节点密度低时，定位精度较低，当未知节点可感知的锚节点数小于3或节点数不小于3且不存在符合PIT测试的三角形时，无法进行APIT定位。故在锚节点稀疏时APIT算法的定位覆盖率是很低的。

图1 两种误判情况Fig 1 Two situations of misjudgement

3)在求三角形约束区域交集质心时，算法复杂度高，效率低下。

1.3 APIT—HR 算法设计

针对APIT算法存在上述缺陷，本文提出APIT—HR质心定位算法。算法做以下完善:1)以面积规则定性的判断是否存在InToOut和OutToIn错误;2)以圆交域质心定位算法提高定位覆盖率;3)以RSSI值折半区域法代替三角形约束区域交集质心法，降低计算复杂度。

1.3.1 面积规则

针对判断一个点是否在三角形内部，本文采用面积规则来判断，即外部较大三角形面积等于3个内部较小三角形面积和。由信号损耗模型可知距离值和RSSI差值是一一对应的正函数关系，故可用RSSI差值代替距离值作定性分析。设三角形3个顶点为A，B，C，未知节点为U，则它们之间距离值 dAB=|RSSIBA-RSSIAA|，dAC=|RSSICARSSIAA|，dBC=|RSSIBC-RSSICC|，其中，RSSIij表示 i节点感知 j节点的RSSI值，若i=j，则根据功率和RSSI关系转换求得，WSNs中节点是同规格的。

由△ABC的面积SABC如式(4)所示

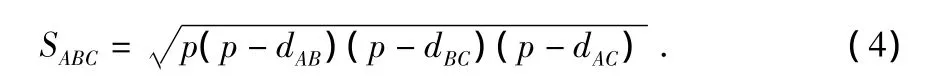
类似的，可求SABU，SACU，SBCU，若满足面积规则，判定 U点在△ABC内，否则，在△ABC外。

1.3.2 APIT—HR定位算法

APIT—HR算法流程图如图2所示，步骤如下:

1)初始化网络，锚节点返回自己被未知节点感知确认消息。

2)未知节点将可感知的锚节点存入锚节点集合M_set(数组构成)中。从M_set任取不重复的3个锚节点组成三角形，并执行PIT测试［10］，若未知节点在三角形内，则把该组合存入三角形集合T_set中;否则，舍弃。

3)若T_set为空，执行圆交域质心定位算法;否则，从T_set中取出一个元素，执行区域缩减与质心坐标求解，步骤如下:

a.取T_set一个元素，设三角形顶点为A，B，C，未知节点为U，然后取A，B，C的3个顶点中的1个(设为A)作为圆心，同时，余下的2个顶点B，C和未知节点U分别把各自感知圆心处锚节点的RSSI值(设为RSSIBA，RSSICA，RSSIUA)报送给圆心锚节点，再分别用与 RSSIUA比 较。若 RSSIUA＞，则说明U在以A点为圆心，半径为的圆与三角形交汇区域;若，则说明U在以A点为圆心，半径为的圆与三角形交汇区域;若，则说明以该点为圆心的圆约束不了U。

b.重复步骤(a)，其他2个锚节点进行类似处理。若约束圆个数为0，如图3(a)所示，则将三角形质心作为初步定位坐标;若约束圆数等于1，则把该圆与三角形交汇区域的质心作为初步定位坐标。如图3(b)所示，未知节点被1个圆约束，求Sa1或Sa2区域质心。若约束圆数(圆心不同的圆)等于2，则求这2个约束圆交域与三角形的交域的质心作为初步定位坐标，如图3(c)所示。

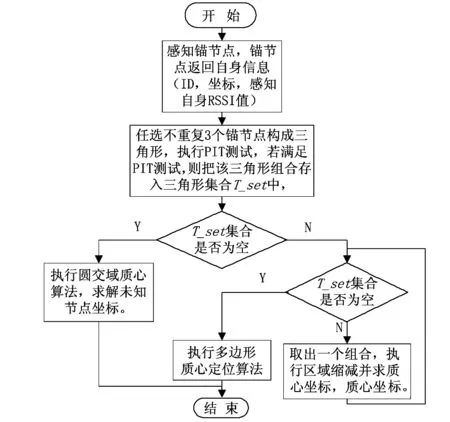
图2 APIT—HR算法流程图Fig 2 Flow chart of APIT—HR algorithm

4)由步骤(3)中的初步定位坐标组成多边形，然后求多边形质心作为未知节点定位结果。

2 仿真实验与分析

为了验证APIT—HR算法的性能，以Matlab对算法进行仿真。仿真环境为200 m×200 m的正方形区域随机部署500节点，随机选派未知节点。为降低偶然性误差，以100次实验均值为结果。以锚节点个数变化来对比分析APIT—HR和原始的APIT算法性能。

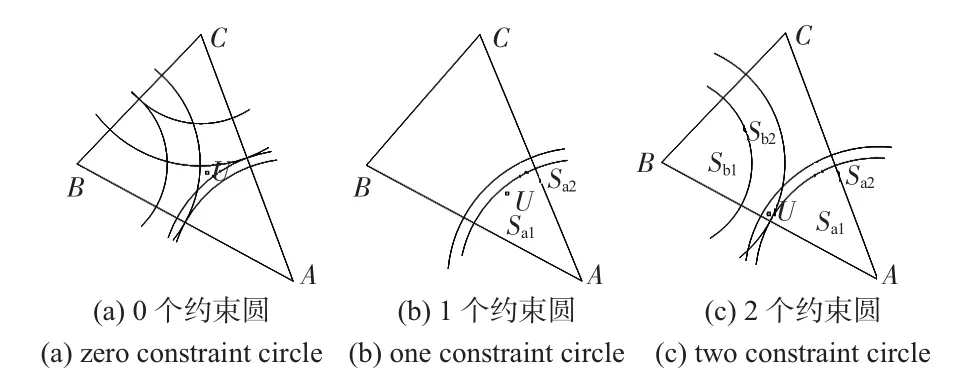
图3 约束圆示意图Fig 3 Diagram of constraint circles

2.1 定位覆盖率分析

定位覆盖率与锚节点数关系如图4所示。当锚节点数小于100时，而 APIT—HR定位覆盖率比 APIT算法高出20%左右。当锚节点数大于100时，APIT—HR的定位覆盖率达到86%左右，比APIT高出约17%。这说明APIT—HR算法的定位覆盖率总体上都要比原APIT算法好。

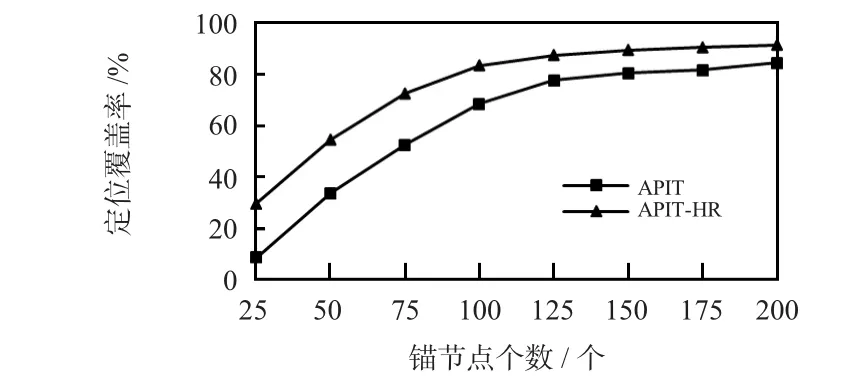
图4 锚节点个数和定位覆盖率关系Fig 4 Relationship between localization coverage rate and number of beacon nodes

2.2 定位误差分析

定位误差和锚节点数关系如图5所示。当锚节点数在25左右时，APIT—HR算法的定位误差比APIT大，这是因为引入的圆交域质心定位算法定位精度差。当锚节点数在50左右时，两种算法定位误差相当。而随着锚节点数继续增加，APIT—HR算法优胜于APIT，这是由于使用了本文提出改进措施减少了InToOut和OutToIn error出现，同时又以RSSI值折半比较对未知节点存在区域进行缩小。从图6看出:在锚节点个数较少时，APIT—HR算法的定位最大误差比APIT算法大，而后最大误差都渐渐减小，并明显优于APIT，这得益于区域缩减方案。

图5 定位平均误差Fig 5 Location average error

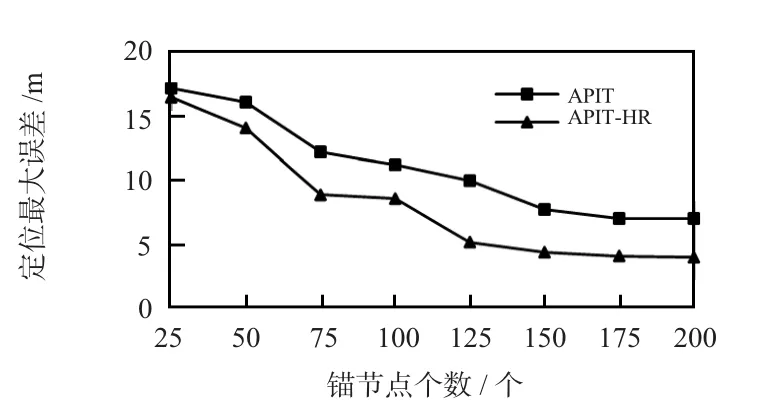
图6 定位最大误差Fig 6 Location maximum error

3 结论

本文以经典的APIT质心定位算法为基础，针对该算法存在的问题进行改进，提出APIT—HR算法。通过仿真实验，对比原始的APIT算法在计算复杂度和定位误差方面的优劣。结果显示:APIT—HR克服锚节点数量较低情况下无法定位问题，同时根据RSSI值缩减未知节点存在区域，提高定位精度。APIT—HR算法在计算复杂度和定位精度均达到理想效果，计算复杂度明显降低，定位误差缩减了22.8%，是一种性能优良的质心定位算法。

［1］金 辉.位置服务和移动定位技术研究［D］.南京:东南大学，2006.

［2］赵 锐，钟 榜，朱祖礼，等.室内定位技术及应用综述［J］.电子科技，2014(3):154-157.

［3］信召建，胡 屏，王 玲，等.基于RSSI值的WSNs节点测距算法改进和定位实现［J］.传感器与微系统，2014，33(6):133-136.

［4］王佩琦，李艳萍，陈相南，等.基于RSSI距离修正的WSNs定位算法［J］.传感器与微系统，2014，33(5):135-137.

［5］肖 竹，谭光华，李仁发，等.无线传感器网络中基于超宽带的TOA/AOA联合定位研究［J］.计算机研究与发展，2013，50(3):453-460.

［6］杨小凤，陈铁军，刘 峰.基于TOA-DOA联合估计的无线定位新方法［J］.数据采集与处理，2014，29(6):1036-1040.

［7］花 超，吉小军，蔡 萍，等.基于RSSI差分修正的加权质心定位算法［J］.传感器与微系统，2012，31(5):139-144.

［8］刘 瑾.基于测距的无线传感器网络的定位算法的研究［J］.航空计算技术，2009，39(6):124-126.

［9］陈锐标.无线传感器网络APIT质心定位算法研究［D］.广州:暨南大学，2008:24-32.

［10］戴佩华，薛小平，邵玉华.基于垂直平分线的区域定位算法［J］.计算机工程，2009，35(2):105-108.

［11］周四清，陈锐标.无线传感器网络APIT定位算法及其改进［J］.计算机工程，2009，35(7):87-89.