锂离子电池新型SOC安时积分实时估算方法

邓 涛，孙 欢

(重庆交通大学机电与汽车工程学院，重庆 400074)

电池荷电状态SOC(state of charge)估算作为动力电池技术研究的一个核心关键问题已经成为企业、科研院所关注的热点［1－5］。由于在实际估算时受到诸如电压、电流、温度、内阻等因素的影响，SOC值很难直接由电池本身得到，只能通过其影响因素间接推算出来。而这些影响因素又是随着电池使用情况变化的，中间存在许多不确定因素，因此为动力电池SOC实时估算带来巨大的困难。如何确定一种精确且能实时估算SOC的方法成为电池技术的一个难点。当前已有的诸多传统SOC估算方法都存在精确度不高等不同程度的缺陷，一些先进的SOC估算方法虽能保证精确度，但运算量大，对硬件要求较高，导致成本成倍增加，所以企业的研发热情较低。

传统的开路电压法很难单独进行SOC动态估算，但是可以较精确地得到电池初始SOC状态。安时积分法虽然能实时估算电池SOC，但是很难精确得到电池初始SOC状态。因此考虑将开路电压法与安时积分法结合起来，前者用于估算SOC初始状态，后者用于SOC实时估算。在电池放电过程中，由于内阻的存在，负载电压和开路电压必定不相等。在放电过程中可以用负载电压法估算出SOC用于修正开路电压法和安时积分法得到的SOC，这使得估算结果更加精确。基于此，本文提出一种将安时积分法、开路电压法、负载电压法3种方法结合起来，综合考虑对充放电效率、温度等因素的补偿措施的新型安时积分法来估算动力电池SOC。该方法对硬件要求较低，但估算精度较高，在满足SOC估算需求的情况下节约了成本［6］。

1 新型SOC安时积分实时估算方法

动力电池SOC是反映电池剩余电量的一个重要参数，通常人们通过电量来定义电池的SOC。电池的荷电状态是电池剩余容量占电池容量的比值。

式(1)中:Q为电池的消耗电量;QN为电池额定容量。

1.1 开路电压法

锂离子电池在其性能完全稳定时，它的荷电状态与它的开路电压在一定范围内有线性关系，而且这种线性关系受到温度和电池老化因素的影响很小，所以在电池开始充放电时，在满足一定条件下，可以通过检测电池两端的开路电压得到电池的初始容量SOC0［7］。则

式(2)中:U0为电池开路电压;m和n为系数。

1.2 安时积分法结合开路电压法

结合开路电压法和安时积分法估算 SOC，则有

式(3)中:QN为电池的额定容量;I为充放电电流(充电时电流为负值，放电时电流为正值);K为与温度和充放电效率因子有关的常数，

其中:Kt为温度修正系数;η为充放电效率因子，可以由Peukert方程求得。

1)Kt的确定

目前常用的温度补偿公式为［8］

式(5)中:Ta为标准温度;T为设定温度。

2)η的确定

由Peukert方程可得可用电量与放电电流存在的关系公式为

式(6)中:I为放电电流;A为与活性物质有关的电池常数。只要初始条件相同，则A和n是相同的，所以

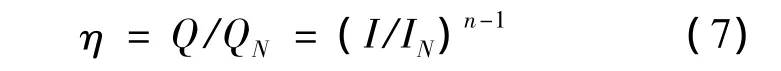
式(7)中IN为额定电流。只要测出两组Q和I就可以求出A和n(n为与电池结构特别是极板厚度有关的常数，其值为1.15～1.42)。Peukert方程表明放电电流越大，电池容量越小，当电池电流很小时就不适用了。但是本文是锂离子电池，放电电流一般比较大，所以 Peukert方程适用［9－10］。

1.3 负载电压法

基于采用开路电压估算SOC的方法，可以采用负载电压法来估算SOC，其原理如图1所示。在电池组内阻和电流已知的情况下求出负载两端的电压，此时的负载电压在电池性能稳定时同样与它的荷电状态呈一定的线性关系。此方法在理论上弥补了开路电压法不能实时估测SOC的缺点，因此当电池处于放电状态时，可以通过其负载端电压来估算电池的SOC1。当放电超过一定时间时，可以用端电压预测的SOC1来校正前面用安时积分法结合开路电压法求得的SOC。

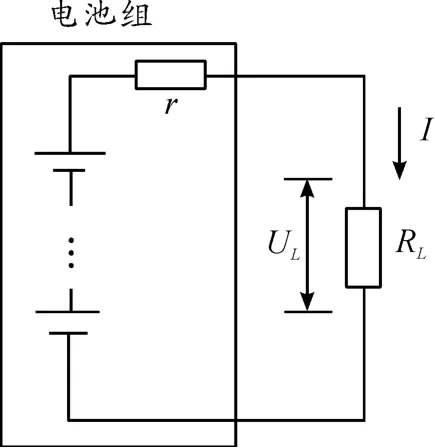
图1 负载电压法原理

1.4 新型安时积分实时估算SOC

由式(2)和(6)可得

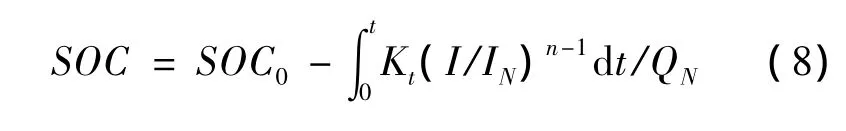
式(8)是安时积分法结合开路电压法，再考虑温度和充放电效率估算出的电池荷电状态。而由本文可知可用负载电压法预测得的SOC1来校正式(8)求得的SOC，从而得到最后结果:

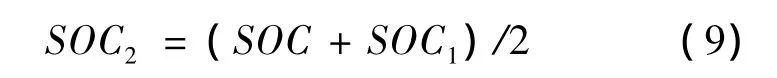
本文以安时积分法、开路电压法、负载电压法结合为主，并且综合考虑对充放电效率、温度等因素的补偿措施来估算电荷状态。此方案实验阶段需要测量的参数有开路电压、负载电压、恒定充放电电流、充放电时间、温度。而在实际使用中需要测量的参数有开路电压、负载电压、动态电流、温度。新型SOC安时积分实时估算流程如图2和图3所示。

2 新型SOC安时积分实时估算方法建模仿真

2.1 SOC估算建模

根据SOC估算流程，利用Simulink工具包分别建立了SOC估算充放电模型。

SOC估算充电模型如图4所示，其中add的上面部分是根据开路电压与SOC关系曲线构造的经验公式建立的，通过开路电压得到电池SOC并且输出;add的下面部分是通过安时积分法建立的，输入变量为电流，通过积分计算出SOC并且输出［11－12］。

图2 SOC放电估算流程

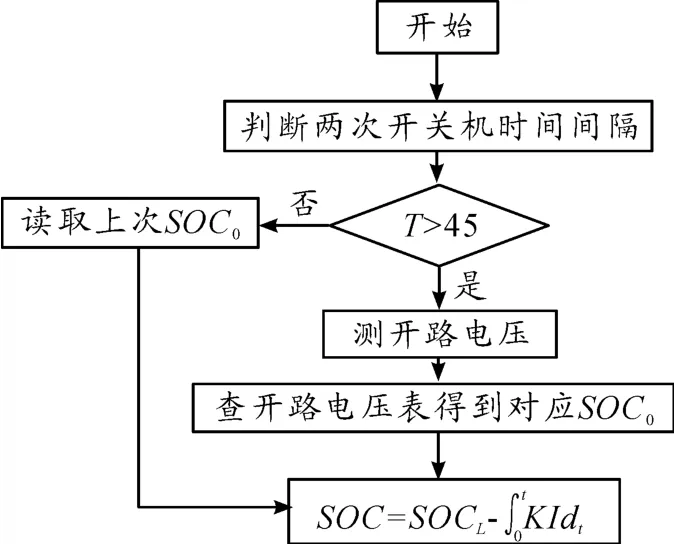
图3 SOC充电估算流程

SOC估算放电模型如图5所示，其中add左边同充电模型相同，add右边是根据负载电压与SOC关系曲线构造的经验公式建立，通过负载电压得到电池SOC，对左边求得的SOC做一个简单的修正。

2.2 仿真分析

假设电池的工作温度为25℃，SOC充放电模型分别在1 C的恒定电流下进行充放电仿真，其输出SOC曲线如图6所示。由图中可以看出，该模型充放电输出的SOC曲线都为线性的，这是因为进行SOC仿真时将温度和充放电电流设为定值，该线性SOC曲线是符合本文估算方法的。但是电池实际工作过程中SOC的估算受到电流、温度、内阻、电压等因素影响，电池实际工作SOC曲线应该是波动的，因此仿真曲线必定和实际实验曲线不同，即仿真结果和实际结果存在一定误差。

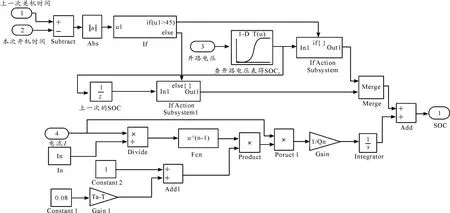
图4 电池充电SOC估算模型

图5 电池放电SOC估算模型

图6 1C恒定电流下充放电仿真结果

3 新型SOC安时积分实时估算方法试验

为验证提出的新型SOC安时积分实时估算方法的准确性和实用性，搭建锂离子电池充电实验平台进行SOC估算方法验证实验。整个实验台包括电池测试系统、实验电池系统、数据采集系统等。锂离子电池实验台负责给动力电池充电以及吸收电池放出的能量。锂离子电池实验台采集的电池数据通过 RS485上传到控制计算机［13－15］。实验台布置如图7所示。

图7 锂离子电池充放电实验台

电池的开路电压特性通过《PNGV电池试验手册》［11－12］中的 HPPC 实验获得。实验方法如下:①用恒流0.5 C限压3.6 V将电池充满;②用1 C电流放出10%DOD的电量;③静置1 h;④重复步骤①～③，在电流放出90%DOD处进行最后实验;⑤ 将电池放置到100%DOD;⑥ 静置1 h。开路电压是在不同SOC电池HPPC实验之间的搁置时间末测量得到。

开路电压的特性是指电池开路电压与放电电流、电池工作温度和电池容量的函数关系。这种函数关系可表示如下［13］:

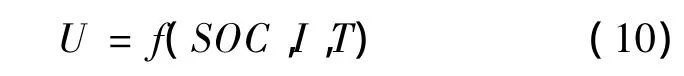
充电实验:在25℃通风环境条件下，以1 C恒电流放电至电池组容量为30%，搁置30 min，分别以1 C恒电流充电到电池组容量为100%。测量充电时间，计算充电功率，并重点关注总电压、总电流、电池模块电压和电池温度等。结果如图8所示。

图8 锂电池单体SOC与开路电压曲线

放电实验:在25℃通风环境条件下，以1 C恒电流放电至电池组容量为30%，搁置30 min，再以1 C电流进行恒电流充电到电池组容量为100%，搁置30 min，然后以1 C电流进行恒电流放电到电池组容量为30%，测量充电时间，计算充电功率，并重点关注总电压、总电流、电池模块电压、电池温度等。结果如图9所示。

图9 电池充电电压、电流

通过电池充放电实验采集到充放电过程中的电流电压，计算得到电池SOC并绘制其与时间关系的SOC曲线。对比分析仿真和实验结果，可得充放电SOC随时间变化的曲线，如图10所示。

图10 电池放电电压、电流

对仿真实验结果和电池充放电实验结果进行比较，可以计算出利用新型实时安时积分法估算的电池SOC的相对误差，计算公式为

通过计算得到的相对误差可以绘制出新型安时积分法估算SOC的相对误差曲线，如图11和12所示。

由SOC相对误差曲线可见:在充电过程中，SOC在30% ～50%，相对误差变化较大，但是也基本保持在3%以内;SOC在50% ～95%，其相对误差基本在1.5%以内;放电过程其SOC变化也基本在3%以内。图12表明，新型实时安时积分可以较精确地估算出电池当前的SOC状态［16－17］。

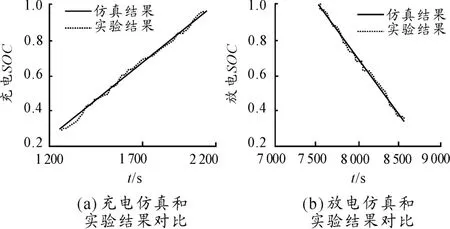
图11 充放电输出仿真与实验所得SOC曲线

图12 SOC相对误差曲线

4 结束语

本文根据传统安时积分法、开路电压法及负载电压法，综合考虑充放电效率、温度等因素的补偿措施，提出了一种新型实时安时积分法来估算动力电池SOC。搭建了SOC充放电仿真模型，通过仿真得到了充放电SOC线性曲线，从理论上验证了该方法的可行性。搭建了锂离子电池充放电实验平台对动力电池进行了充放电实验，记录充放电过程的电压、电流等信息，计算出不同时段的SOC值并且绘制出充放电SOC曲线。通过仿真结果和实验结果的对比，计算出SOC相对误差并绘制曲线，表明其误差偏差基本在3%以内，证明了新型实时安时积分法具有较高的精确度。

［1］胡林，谷正气，黄晶，等.电动汽车的关键技术分析［J］.机械制造，2005，43(10):43－45.

［2］何代杰，王泽京，李庆东，等.微型纯电动汽车电池管理系统的设计与研究［J］.西南大学学报:自然科学版，2012，34(9):136－140.

［3］赵国才，周莎.重庆市电动汽车商业运行模式［J］.重庆理工大学学报:自然科学，2014(4):15－23，49.

［4］赵孟娜，米林，冯勇.基于神经网络的二次开发电动汽车电池SOC测试软件设计［J］.四川兵工学报，2012(8):95－98.

［5］仝瑞军，张志国，张泱渊.一种新型纯电动城市客车锂电池组的PACK及管理［J］.客车技术与研究，2013(6):35－37.

［6］曹贵华，陈智家，王卓.镍氢动力电池SOC估算方法［J］.汽车工程师，2009(9):41－44.

［7］李司光，张承宁.锂离子电池荷电状态预测方法研究［J］.北京理工大学学报，2012(2):2－4.

［8］Oshitani M，Watada M，Kaorietal S D.Effect of Lanthanide oxide additives on the high temperature charge acceptance characteristics of pasted nickel electrodes［J］.Journal of the Electrochemical Society，2001，148(1):A67－A73.

［9］Xiaosong Hu，Fengchun Sun，Yuan Zou.Comparison between two model-based algorithms for Li-ion battery SOC estimation in electric vehicles［J］.Simulation Modeling Practice and Theory，2013(34):1－11.

［10］Yao He，XingTao Liu，ChenBin Zhang，et al.A new model for State-of-Charge(SOC)estimation for high-power Liion batteries ［J］.Applied Energy，2013(101):808－814.

［11］吴友字，肖婷，雷冬波.电动汽车用动力镍氢电池SOC建模与仿真［J］.武汉理工大学学报，2008，30(1):55－58.

［12］Minxin Zheng.Dynamic model for characteristics of Liion battery on electric vehicle［Z］.［S.l.］:ICIEA ，2009:2967－2870.

［13］胡建军，税江，秦大同，等.混合动力电动汽车NIMH电池放电性能试验分析［J］.重庆大学学报，2006，30(10):2－6.

［14］胡明辉，秦大同.混合动力汽车镍氢电池组的充放电效率分析［J］.重庆大学学报，2009，32(3):279－282.

［15］Alliance B E.Battery test manual for plug-In hybrid electric vehicles revision［J］.Department of Energy National Laboratory，2008(3):22－29.

［16］蒋新华.锂离子电池组管理系统研究［D］.上海:中国科学院上海微系统与信息技术研究所，2005:79－80.

［17］Sato N，Ya K.Thermal Behavior Analysis of nickel metal hydride batteries for electric vehicles［J］.JSAE Review，2001(21):205－211.