模拟电路单故障与多故障诊断的提升小波和RBF方法
隆腾舞,刘红,邢永桢,高学潮,王琪
(长春理工大学 光电工程学院,长春 130022)
为了保证电子仪器等设备的正常运作,模拟电路故障诊断技术起着关键作用,但由于模拟电路输出响应的连续性,且受到非线性、容差性等因素的制约,模拟电路故障诊断已成为现代电子系统发展的瓶颈问题,是电子系统进一步向集成化迈进亟待攻克的技术难关,所以及时发现故障并保证系统能够安全、可靠地运行已成为现今比较重要的课题之一[1]。近几十年来,国内外专家学者不断攻关,相继提出了模糊理论[2-4]、遗传算法[5,6]、神经网络[7-10]、小波分析[11-14]等现代故障诊断的方法,并取得了良好效果。但上述方法主要对象为电路中的单一故障,对电路中多故障的诊断尚未过多涉及。本文提出了基于提升小波和RBF神经网络算法的故障诊断方法,不仅实现了单故障的高效、精确诊断,而且可以实现模拟电路的多故障诊断。
1 提升小波
提升小波是由Sweldens等人提出的,它与传统小波的区别在于不对傅里叶变换产生依赖,只需要在时域内就可以完成小波变换。基于Mallat算法的传统小波变换的思想为:在分辨率为2m的情况下,信号 f的近似系数为Am,那么,Am能够继续分解成 f在分辨率为2m-1下的近似系数Am-1和在分辨率为2m-1与2m之内的细节系数Dm-1之和。相比于传统小波,提升小波算法十分简单,且运算速度迅速、对内存的需求小、能够本位操作进行运算。提升小波变换过程由分裂、预测、更新三步组成。
(1)分裂:分裂(Split)是将原始信号 sj={sj,k}分裂为两个平行的子集,大多是分裂成奇数序列oj-1和偶数序列ej-1,且分裂后子集的空间长度是原来的一半,即:

(2)预测:预测(Predict)是根据奇数序列与偶数序列具有相关性这一特点,就可以用一个序列来预测另一个序列(通常是用偶数序列ej-1来预测奇数序列oj-1)。P(⋅)为预测器。预测结果为细节信号,过程如下:

(3)更新:原始数据在分裂过程后形成的子集,其某种整体的特性或许与原始数据不相符,为了使原始数据的这些特性得以维持,所以更新(Update)步骤必不可缺。其中U(⋅)为更新器,过程如下:

式中,sj-1为sj的低频部分。构成故障的N维特征向量
有时由于得到的特征向量集的数量级有比较大的差别,所以需做归一化处理。
信号sj经过提升小波变换后,被分解为低频信息sj-1和高频信息dj-1;再次通过分裂、预测和更新,低频部分sj-1则再一次被分解为低频信息sj-2和高频信息dj-2;照此类推,原始信号sj通过n次分解后,其小波表示方法为{sj-n,dj-n,dj-n+1,…,dj-1}。小波提升过程如图1表示,其中 P(⋅)为预测器,U(⋅)为更新器。
提升小波与传统小波相比,由于提升小波在提升计算过程时,是采取了替换的方法,所以能够节省丰富的空间;对子表达式的反复利用,在很大程度上减少了运算,因此在工作效率上有了大大的提升。
利用提升小波来求取故障电路的特征向量集,其本质是对故障电路的输出响应作多层提升小波分解,得到低频和高频信号,再将能够表达各种故障的频率集合提取出来,作为故障的特征向量集。其过程为:
(1)选择合适的提升小波基,对各种故障的输出响应信号进行N尺度分解。
(2)提取每层的低频系数cai(i=1,…,N),组成N层低频系数的集合{ca1,ca2,…,caN}。
2 RBF神经网络

图1 提升小波过程
RBF神经网络又叫径向基函数神经网络,结构类型是前馈网络。此网络的结构由输入层、隐含层、输出层三部分组成。因其以径向基函数作为隐含层单元而得名,基函数的功能是将输入数据从低维空间映射到高维空间,解决原来数据线性不可分问题。由于它结构十分简单、训练步骤迅速且与初始权值无关,所以在模拟电路故障诊断中将其作为分类器具有十分理想的效果。其网络拓扑结构如图2所示。

图2 RBF神经网络拓扑结构

ci为基函数中心,为函数方差。
由于输出层学习速度快,利用线性优化策略来调节隐含层数据的连接权值,可得到输出结果yk(x):

输出向量和输入向量的关系如下:
第i径向基函数模型为:
其中,m是输出个数,wjk是后两层的连接权值。
3 仿真实例
3.1 诊断电路
将本文提出的提升小波和RBF神经网络应用于实际的模拟故障电路诊断。以Sallen-Key带通滤波器作为待诊断电路,如图3所示。其中心频率为25KHz,在Dual-Core 2.1GHz、2G内存的PC机上,ORCAD9.2和MATLABR2009a环境下对电路进行仿真和实现电路故障诊断。
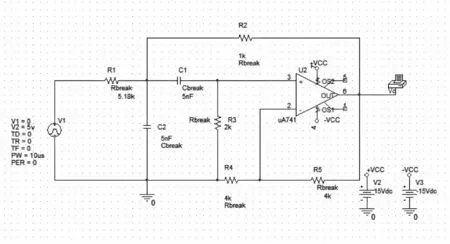
图3 Sallen-Key带通滤波器
在电路中,设电阻和电容的正常容差范围为标称值的5%。本文设定四种单故障和一种多故障。单故障分别为C1偏小40%、R4偏小50%、R5偏大60%,正常情况也属于单故障的一种,多故障为C1偏大40%且R5偏小60%。各种故障类型及编码如表1所示,符号↑代表故障元器件的值偏大,符号↓代表故障元器件的值偏小。
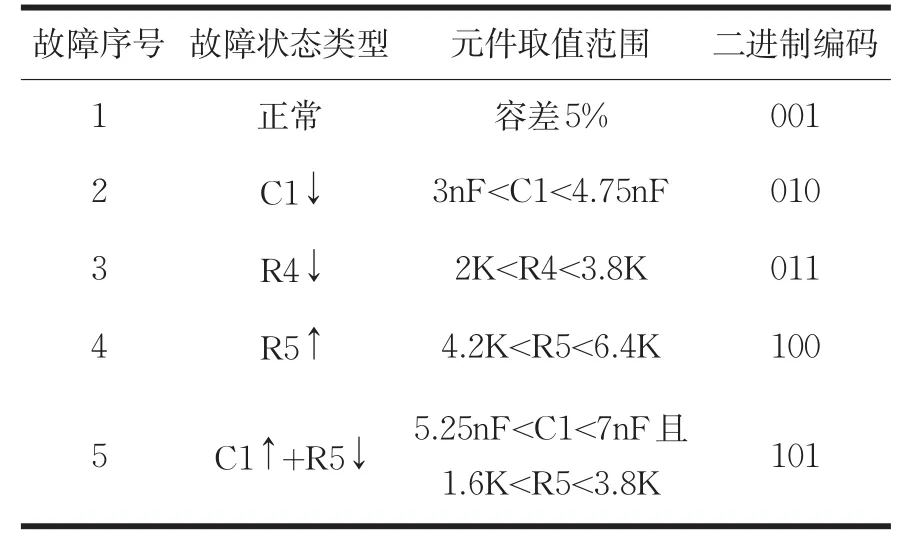
表1 故障集及对应编码
3.2 输出电压提取
用Pspice仿真各种故障状态下的输出响应,激励信号为宽度10μs、幅度5V的单脉冲信号,每种故障各做50次MC仿真,对每一次仿真结果取其200μs内的2001个电压点,采样时间为0.1μs。提取电路输出的原始电压数据,从每种故障的50次MC仿真中各取一次,对五种故障作横向对比,如图4所示。

图4 五种故障输出电压对比图
3.3 特征提取
对每种故障下50次MC仿真用bior1.5小波进行6层提升小波分解,提取6层的低频系数,取每层低频系数的首个元素作为故障电路的特征向量,正常和多故障响应信号6层bior1.5提升小波分解对比如图5所示。可得到每种故障下的50组特征向量,将25组作为训练样本集,训练RBF神经网络,另25组作为测试样本集。表2为提升小波提取的故障特征向量值。

表2 电路故障特征向量值

图5 正常信号和多故障响应信号的6层bior1.5提升小波分解对比图
3.4 训练RBF神经网络
将各种故障的25组特征向量作为训练样本集,训练RBF神经网络。设定神经网络参数:均方误差0,扩散速度4,神经元最大数目75,步距设为5。训练误差收敛曲线如图6所示。

图6 RBF神经网络训练误差收敛曲线图
3.5 故障分类
用上一步训练好的RBF神经网络来诊断每种故障状态的另外25组测试样本,其诊断结果如表3所示。平均诊断率为99.2%,诊断时间为4.3s。
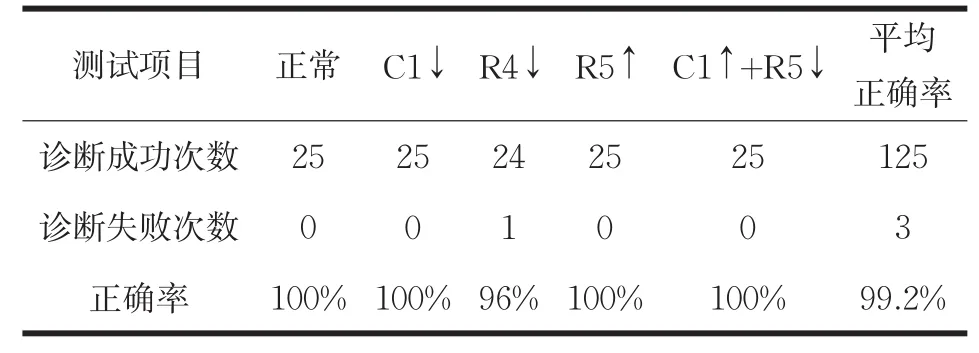
表3 基于提升小波的神经网络诊断结果
3.6 提升小波与非提升小波诊断对比
用提升小波和非提升小波两种不同的方法分别提取特征向量,训练RBF神经网络,诊断故障电路。其诊断结果对比如表4所示。

表4 提升小波和非提升小波诊断结果对比
可知,提升小波对各个故障电路的低频部分能更好的区分,有效的提高了故障诊断率,减少了故障诊断时间。和RBF神经网络的结合,使得诊断效果十分理想。
4 结论
本文提出了提升小波和RBF神经网络的方法对模拟电路的单故障和多故障进行诊断。通过具体实验,证明了此方法的准确性和高效性。又与传统小波做横向对比,表明提升小波在诊断效率上更优于传统小波。
[1]杨士元,胡梅,王红.模拟电路软故障诊断的研究[J].微电子学与计算机,2008,25(1):1-7.
[2]Wang P,Yang S Y.A new diagnosis approach for handling tolerance in analog and mixed-signal circuits by using fuzzy math[J].IEEE Trans.on CAS I:Regular Papers,2005,52(10):2118-2127.
[3]Catelani M,Fort A.Soft fault detection and isolation in analog circuits:some results and a comparison between a fuzzy approach and radial basis function networks[J].IEEE Trans Instrum Meas,2002,51(2):196-202.
[4]彭刚,彭敏放,何怡刚.基于聚类模糊神经网络的非线性电路故障诊断[J].微电子学与计算机,2006,23(8):1-3.
[5]彭敏放,何怡刚,沈美娥,等.基于多目标遗传优化的容差电路故障屏蔽诊断[J].电工技术学报,2006,21(3):118-122.
[6]He Y G,Li Y,Liu M R.BP neural network approach to module fault diagnosis for large analog circuit[C]//Proc.ofTENCON 2004.IEEE Region 10 Conference,2004:395-398.
[7]郭珂,伞冶,朱亦.基于PSO-RBF神经网络的模拟电路故障诊断研究[J].电子设计工程,2011(24):17-23.
[8]乔俊飞,韩红桂.RBF神经网络的结构动态优化设计[J].自动化学报,2010,24(1):865-872.
[9]Simon Haykin.Neural networks and learning machines[M].China Machine Press,2011.
[10]宫玉琳,文大化,张静鹤.基于粒子群优化算法和RBF神经网络的水质评价方法研究[J].长春理工大学学报:自然科学版,2014,37(5):141-145.
[11]Aminian M,Aminian F.A modular fault diagnostic system for analog electronic circuits using neural networks with wavelet transform as a preprocessor[J].IEEE Trans Instrum Meas,2007,56(5):1546-1554.
[12]曹颖.基于粒子群算法的模拟电路故障诊断[D].长春:长春理工大学,2013.
[13]杨青,田枫,王大志,等.基于提升小波和递推LSSVM的实时故障诊断方法[J].仪器仪表学报,2011,32(3):596-602.
[14]宋国明,王厚军,刘红,等.基于提升小波变换和SVM模拟电路故障诊断[J].电子测量与仪器学报,2010,24(1):17-22.

