求解多目标柔性作业车间调度问题的离散人工蜂群算法

田野，徐洪华

（长春理工大学 计算机科学技术学院，长春 130022）

作业车间调度问题（Job Shop Scheduling Problem，JSSP）是一类典型的组合优化问题，描述为若干工件在一组机器上的加工过程，每个工件都包含一系列操作，要求任一时刻一台机器最多可加工一个工件，并且这些操作必须按照规定的顺序进行加工，目的是要找出一个适当的调度方案，使特定的目标（如最终加工时间）得以满足［1］。相对于JSSP问题，柔性作业车间调度问题（Flexible Job Shop Scheduling Problem，FJSSP）允许每个操作可以从给定的机器集合中选择任意机器进行加工，因此柔性作业车间调度问题是作业车间调度问题的扩展，并且更为复杂［2］。人工蜂群算法（Artificial Bee Colony Algorithm，ABC）是一种新的群智能算法，主要通过模拟蜜蜂的觅食行为来进行问题的求解［1］。该算法思想简单、参数少、易于实现，目前已在函数优化、生产调度等领域得到了广泛的应用［3-5］。

本文提出了一种离散的人工蜂群方法（Discrete Artificial Bee Colony Algorithm，DABC）用于求解柔性作业车间调度问题。为了使得人工蜂群算法可应用于组合优化问题的求解，算法通过交叉方式来搜索更好的蜜源，并引入食物源活性来进行自适应的变异，以降低早熟收敛的可能性，增加群体的多样性。

1 问题描述

柔性作业车间调度问题假设有n个待加工的作业集合J={J1,J2,…,Jn}和m台可用于作业加工的机器集M={M1,M2,…,Mm}，每个作业i包含ni个操作，Oi,j(j=1,2,…,ni)表示作业i的第 j个操作。Pi,j,k为作业i的第 j个操作在机器k上的加工处理时间（i=1，2，…，n ；j=1，2，…，ni；k=1，2，…，m）。每个作业的每个操作Oi,j可能有多台可以加工的机器集合Mi,j⊆M，Ci表示作业Ji的完成时间。

对于多目标柔性作业车间调度问题来说，需要确定两个子问题，及机器指派问题和作业排序问题，使得预先确定的多个调度目标达到最优。在本文中，有三个调度目标同时优化（最小化），分别是最大完成时间CM、机器总的负载时间WT、以及最大机器负载时间WM。那么对于n个作业，m台机器的FJSSP问题，三个调度目标可以通过下面的数学公式来表述：

其中ω1、ω2和ω3分别成为最大完成时间、机器总的负载时间和最大机器负载时间的权重，且ω1+ω2+ω3=1。

2 DABC算法

2.1 食物源的表示

标准的人工蜂群算法是在连续型空间中进行求解的，因此无法直接用于本文中的问题。因此需要先进行一定的编码，以满足调度问题的需要。文中采取机器指派和操作排序相结合的编码方式，整个编码分为两部分，第一部分是机器指派，用于选择作业所需的加工机器，第二部分是操作排序，用来确定操作的加工顺序。

假设有三个作业，其中作业1和作业2有两道工序，作业3有三道工序，具体编码形式如图1所示。

图1 编码

机器指派中的第一个数字2表示机器2被选定加工工序O1，1，第二个数字1表示机器1被选定加工工序O1，2，以此类推。作业排序中的数字出现顺序表示每个作业的工序加工顺序，如第一个数字2表示作业2的第一道工序O2，1，第二个数字1表示作业1的第一道工序O1，1，第四个数字1表示作业1的第二道工序O1，2，以此类推。

2.2 交叉操作

在标准的人工蜂群算法中，食物源的搜索方式是通过两个食物源位置的差分进行扰动来实现的。而对于求解离散问题时，标准的人工蜂群算法搜索策略无法直接应用于离散问题，但是可以借鉴遗传算法的思想，通过交叉操作来产生新的解，其中雇佣蜂和跟随蜂都采用交叉的方式来获得新的食物源位置。

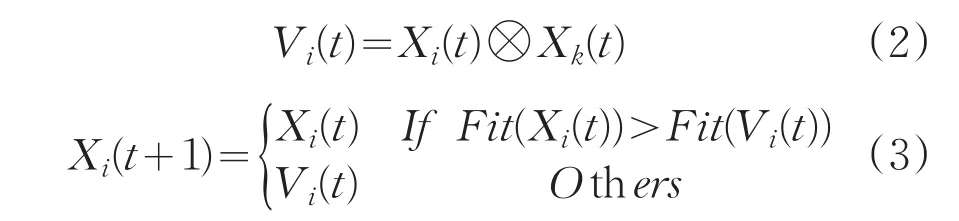
根据上面的公式可以看出，通过交叉操作后，解Xi(t)既受到了解Xk(t)的扰动，同时也保留了自身的一部分信息。针对柔性作业车间调度问题的特点，文中针对机器指派序列采用多点交叉（Multiple Point Crossover，MPC），该交叉操作能够较好地继承父代个体工序分配的机器特征性到子代。相对于作业排序的交叉操作，本文在两点间作业段交叉的基础上提出了一种两点间作业段随机移动的交叉方法，称为 Randomly Movement Crossover（简称RMC），RMC交叉和两点间作业段交叉的不同之处在于两个切点之间的作业子排列可以放置在子代中的任何位置，只要保证子排列在两个子代个体中的位置是互相对称的即可，因此可以保证即使交叉的父代个体相似或甚至相同，也能得到不同于父代特征的子代个体，如图2所示。

图2 RMC交叉示意图

从图2中可以看出，当两个父代个体差异性很小甚至相同时（右侧），RMC交叉仍然可以得到不同的子代个体。

2.3 变异操作

在发现食物源的过程中，所有食物源的位置会逐渐向目前发现的最优食物源靠拢，当所有的食物源汇聚到一起时，由于差分扰动无法起作用，因此容易导致算法的早熟收敛，陷入局部极值。对于这种情况，本文采用变异操作来克服这个问题，通过对当前食物源进行自适应变异来增强群体的多样性，避免陷入局部极值。具体而言，在食物源的发现过程中，考虑当前食物源和目前发现的最优食物源之间的差异性，根据这个差异性来确定食物源的变异概率，进行自适应变异。这个差异性文中称为食物源活性，首先给出食物源活性的概念。

食物源活性：对于一个食物源位置Xi，其活性Activity（Xi）定义为当前食物源位置和当前最优食物源位置之间的差异度。

由于食物源的位置表示成作业的排序序列，因此很容易出现多个食物源对应的作业排序不同，但是和当前最优食物源所对应的作业排序序列的差异度相同，即多个食物源的活性是一样的，从而导致无法体现不同食物源的变异差异。因此，再引入一个随机食物源来计算食物源的活性，即：

则食物源的变异概率公式如下：

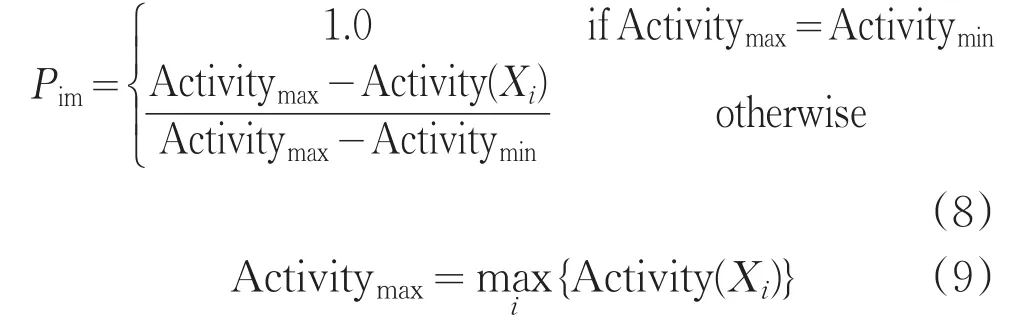
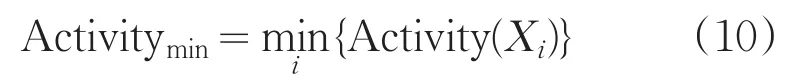
此时，如果食物源活性较好，则认为群体多样性较好，那么食物源可以以较大的概率进行变异；而当食物源活性较差时，则群体多样性差，食物源可能比较密集，并且当前食物源可能更接近最优解，因此应该施以较小的概率进行变异。

在本文中，考虑三种变异方式：交换变异（M1）；插入变异（M2）和反转变异（M3）。三种变异方式如图3所示。

图3 三种变异方式

从图2中可以看出，交换变异的搅动是最小的，而插入变异和反转变异都会对两个随机选择的位置之间的作业产生影响，但是反转变异同时也会改变原有的作业顺序，因此对粒子的搅动更大一些。变异过程的伪代码描述如下：

2.4 算法描述

基于前面几部分的介绍，本文提出的DABC的伪代码描述如下：

3 实验

为了测试DABC算法的性能，在本节中，将文中提出的DABC算法通过常用的Kacem测试集［6］进行了测试，并和文献［7］中的算法（这里称为ESM算法）进行了对比，验证DABC算法的有效性。

3.1 实验环境及参数设置

DABC算法采用MATLAB语言实现，机器配置为Windows 7系统，处理器为Intel Core（TM）i3-2120，3.3GHz，内存大小为4G。

对于DABC算法来说，主要的参数有三个，分别是群体大小NP、食物源废弃阈值limit以及迭代次数gen。群体大小我们固定为200，其中雇佣蜂和跟随蜂的个数分别为100，侦察蜂的个数为1。而limit和gen与问题规模有关，因此文中分别设置为2*n和4*n*m（n是作业个数，m是机器个数）。

3.2 实验结果与分析

在本小节实验中，将本文DABC算法与ESM算法进行比较，遵循文献［6］，权重系数共有9种组合，两个算法的对比结果如表1至5所示。

对于Kacem4X5，ESM算法对于不同系数的组合共找到了三组最优解，而DABC算法找到了两组。而对于问题Kacem8X8来说，ESM算法共找到了四组不同的最优解，而DABC算法只找到了三组，但是DABC算法找到的解的质量要优于ESM算法，如DABC的一组解（16，73，13）要优于ESM算法找到的解（17，73，13）。两个算法对于问题Kacem10X7均找到了三组相同的最优解。DABC算法再Kacem10X10问题上，尽管找到的最优解个数与ESM算法相等，但是其中解（8，42，5）要优于ESM的解（8，42，6）的，而ESM算法仅仅在组合3的情况下发现了解（8，42，6）。对于问题Kacem15X10，除了组合2的情况外，DABC算法找到的最优解均不劣于ESM算法找到的最优解。因此，通过实验可以说明，尽管对于个别问题，DABC算法找到的最优解个数比ESM算法少，但是解的质量不劣于或者优于ESM算法，并且将所有组合获得的最优解作为整体来看，DABC算法的求解质量是优于ESM算法的。

表1 Kacem4X5问题结果

表2 Kacem8X8问题结果

表3 Kacem10X7问题结果

表4 Kacem10X10问题结果

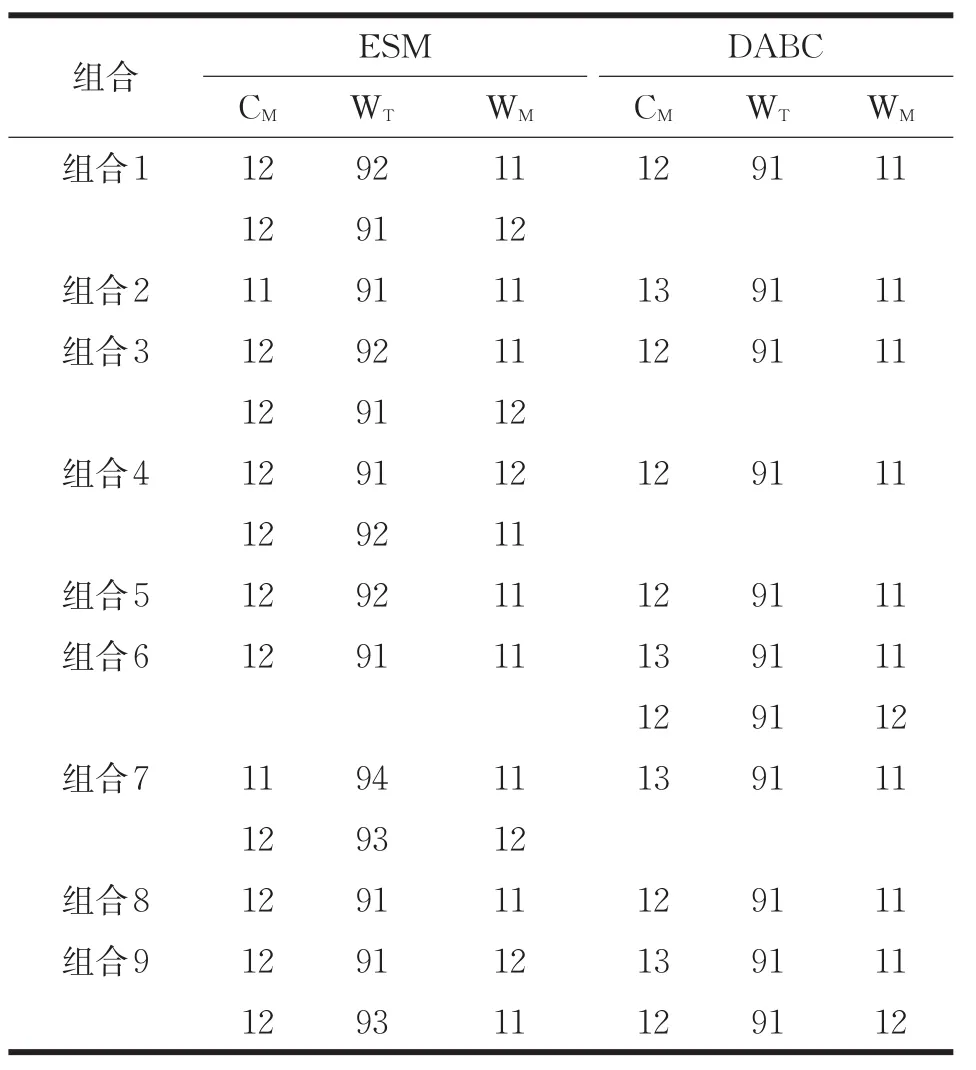
表5 Kacem15X10问题结果

为了更进一步证明前面的结论，文中针对每个问题，将每种组合所获得的最优解进行取均值，即将三个目标值进行相加然后取均值，具体计算公式如下：

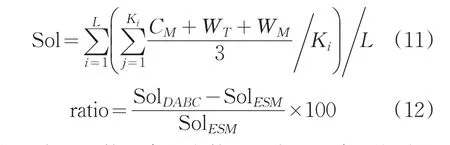
其中L表示系数组合的个数，Ki表示组合i找到的最优解的个数，Sol表示取所有组合获得的最优解的均值，SolDABC和SolESM分别表示DABC算法和ESM算法求得的均值，均值越小，说明获得的三个目标的时间相对越少，ratio表示两种算法的均值相对偏离比。从公式（12）可以看出，如果ratio为负值，说明SolDABC小于SolESM，也就是说DABC算法求得的解的均值要优于ESM算法。表6列出了计算后的均值、算法运行时间以及均值的比较。

表6 最优解均值对比

从表6中可以看出，对于所有测试问题，DABC算法获得的最优解的均值都小于ESM算法获得的最优解均值，ratio的值均为负值，这说明从获得最优解的整体性来看，DABC算法获得的解的质量要由于ESM算法。此外，DABC算法的执行时间也小于ESM算法，因此，DABC算法是有效的，并且是高效的。

4 结论

本文针对柔性作业车间调度问题进行了研究，提出了一种离散的人工蜂群算法DABC用于求解最大完成时间、机器总负载时间和最大机器负载时间问题。算法通过交叉策略来实现解的搜索，并提出了一种两点间作业段随机移动的交叉策略（RMC），该交叉策略在两个父代个体相似甚至相同的情况下，也可以得到不同的子代个体。此外，针对群智能算法容易发生早熟收敛的问题，DABC算法引入了自适应的变异策略，通过食物源的活性来自适应地控制个体的变异，增加群体的多样性。

为了验证算法的有效性，本文采用了不同规模的Kacem测试数据集，并和近年来提出的ESM算法进行了对比，实验结果表明，本文算法在总的求解质量上要优于对比算法，并且算法执行时间更短，是非常有效的。

［1］Garey，MR，Johnson DS，Sethi R.The complexity of flow shop and job shop scheduling［J］.Mathematics of Operations Research，1976（1）：117-129.

［2］BrukerP，Schlie R.Job-shop scheduling with multi-purpose machines［J］.Computing，1990（45）：369-375.

［3］Dervis Karaboga，Bahriye Basturk.A powerful and efficient algorithm for numerical function optimization：artificial bee colony（ABC）algorithm［J］.Journal of Global Optimization，2007，39（3）：459-471.

［4］Gao Weifeng，Liu Sanyang.Improved artificial bee colony algorithm for global optimization［J］.Information Processing Letters，2011（111）：871-882.

［5］Liu Yanfeng，Liu Sanyang.A hybrid discrete artificial bee colony algorithm for permutation flowshop scheduling problem［J］.Applied SoftComputing，2013（13）：1459-1463.

［6］Imed Kacem，Slim Hammadi，Pierre Borne.Pareto-optimality approach for flexible job-shop scheduling problems：hybridization ofevolutionary algorithms and fuzzy logic［J］.Mathematics and Computers in Simulation，2002（60）：245-276.

［7］Xing Lining，Chen Yingwu，Yang Kewei.An efficient search method for multi-objective flexible job shop scheduling problems［J］.J Intell Manuf，2009（20）：283-293.