六自由度微动并联机器人工作空间分析
郭本银,刘钰,苗亮
(中国科学院长春光学精密机械与物理研究所,长春 130033)
机器人工作空间是指机器人末端执行器工作时所能到达的区域,是机器人性能评价的重要指标[1-3]。根据执行器工作时位姿变化等特点,工作空间主要分为可达工作空间和灵活工作空间。可达工作空间是指执行器参考点所能打到的点的集合,灵活工作空间是指指执行器参考点可以从任何方向到达的点的集合,可达工作空间包含灵活工作空间。并联机器人执行器的位姿受多个支链共同决定,这种特殊构型使得并联机器人不存在灵活工作空间。另外,与串联机器人相比,并联机器人虽然有良好的刚度及稳定性,但是工作空间较小,是制约其性能的主要因素,所以对并联机器人特别是微动并联机器人的工作空间进行求解是非常有必要的。
并联机器人工作空间的求解方法主要有两类:解析法和数值法。解析法的代表为Gosselin[4]的几何法,它利用曲面包络原理求解各支链空间边界,再利用曲面求交获得实际工作空间,但是这种方法求解复杂难以实现。数值法是在空间中进行扫描,利用机构的逆解获得当前位姿对应的结构参数,以边界约束条件为判定依据从而获得所有边界点的方法[5,6],该方法是求解并联机器人工作空间的有效方法。
本文以实际研制的微动并联机器人为研究对象,在机构组成及工作原理的基础上分析了影响其工作空间的因素,为反映倾斜调整能力,选择合适的欧拉角表达运动平台的姿态,在此基础上进行了逆解的求解,利用数值法获得了定姿态工作空间和灵活姿态角工作空间。
1 机构组成及工作原理
本文实际研制的微动并联机器人是基于Stewart平台的一种典型的并联机构,如图1所示,由上下两个刚性平台和六个并联的、可伸缩的支杆组成,各支杆两端与上下两个平台相接,通过六个支杆的协调运动实现运动平台的位置和姿态的调整。为了克服传统球铰或万向铰等运动副存在间隙和摩擦等对调整机构运动分辨率不利的问题,一方面在Stewart平台的基础上引入柔性铰链来代替传统的运动副,另一方面在六个支杆中设计位移缩小机构。六条柔性支链成对使用,每对柔性支链轴向成120°均匀分布在运动平台和基座平台之间。单条柔性支链如图2所示,两端各有一个柔性万向铰,靠近其中一端有一个柔性片体,电机克服弹簧拉力的情况下进行位移输入,LVDT位移传感器实时监测位移变化来构成控制闭环,柔性支链两端距离会发生与电机位移成一定关系的微小变化。六路支链的长度变化量共同决定了运动平台相对于基座平台的位姿,从而实现了具有一定运动分辨率的精密调整功能。

图1 六自由度并联柔性精密调整机构示意图

图2 单条柔性支链示意图
2 工作空间约束因素分析
并联机器人的工作空间主要受到三个因素的影响,分别为:
(1)各个支链长度变化限制。每一路支链的长度变化范围须满足lmin≤li≤lmax,lmin和lmax分别表示每一路支链长度所能达到的最小值和最大值。
(2)运动副转角限制。各个支链通过运动副分别于运动平台和基座平台相连,由于本身结构的限制,每个运动副转角须满足 0≤θi≤θmax,θmax为运动副可以达到的最大转角极限。
(3)支链之间的干涉。各个支链在实际设计中有自己的几何尺寸,但是在运动平台行走过程中必须确保各个支链不存在干涉。
对于研究的微动并联机器人来说,目的是实现微米量级和微弧度量级的精密定位,其运动平台的位姿变化与整体尺寸相比非常小,所以可以排除运动副转角限制和支链干涉限制两个约束条件,各个支链长度变化限制作为工作空间的约束条件,其主要由电机的驱动行程、LVDT传感器的量程、柔性片体应力屈服极限等因素决定。其中选取的压电螺纹电机的驱动行程为12.7mm,LVDT传感器的量程为±1.4mm,柔性片体材料为殷钢,屈服极限为276Mpa。利用NX Nastran对单条柔性支链进行有限元分析,殷钢参数表如表1所示,位移云图如图3所示,最终得到的电机位移、LVDT传感器位移、支链长度变化三者之间的关系如图4所示。

表1 殷钢参数

图3 单条柔性支链位移变化云图
由图4可得,电机位移、LVDT传感器位移、支链长度变化三者之间呈现良好的线性关系,制约支链长度变化的因素为LVDT的测量行程,LVDT具有的±1.4mm的量程对应了支链±0.18mm的长度变化,且在LVDT量程内支链最大应力为143.05MPa,在殷钢屈服极限以内。

图4 电机位移、LVDT传感器位移、支链长度变化三者之间的关系
3 工作空间求解
3.1 微动并联机器人逆解
已知运动平台的位姿求解各支链长度变化等结构参数是并联机构的逆解问题,是并联机构运动学分析的重要组成部分[7],也是数值法求解工作空间首要解决的问题。设计的并联机器人机构原理图如图5所示。图中坐标系{P}:Op-XpYpZp为运动平台的坐标系,A1~A6表示运动平台的球铰副,分布在半径为r的平面圆上,α为每对球铰副与坐标系原点及圆心连线的夹角。坐标系{B}:Ob-XbYbZb为基座平台的坐标系,B1~B6表示基座平台的球铰副,分布在半径为R的平面圆上。l为两个球铰副之间的距离即支链的原始长度,h为球铰副在Zb轴方向上的垂直距离。结构参数之间的关系为:
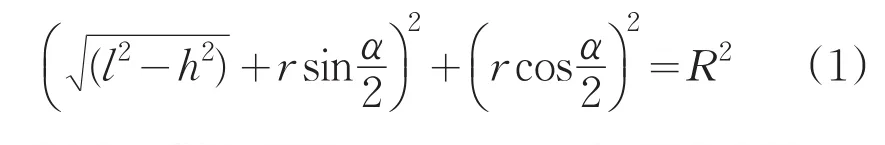

图5 柔性并联机构原理图
为了得到运动平台具有倾斜能力的工作空间,采用直观的欧拉角来描述运动平台的姿态。该变换方法是将动平台坐标系的当前姿态用初始与基座坐标系重合的坐标系通过三次有顺序的旋转而来,如图6所示,旋转顺序为:(1)绕{P} 坐标系的Zp轴旋转角ψ,ψ为最终Zp在{B} 中XbYb平面内的投影与Xb的夹角;(2)绕{P} 坐标系的Yp轴旋转角θ,θ为最终Zp在{B} 中与Zb的夹角;(3)最后再绕{P}坐标系的Zp轴旋转角φ。ψ、θ和φ分别是欧拉角中的进动角、章动角和自旋角。
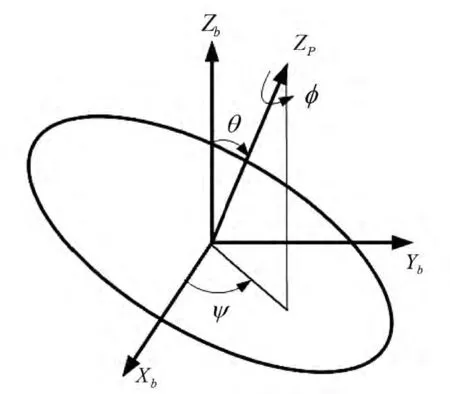
图6 运动平台的欧拉角
设运动平台坐标系原点沿在基座平台坐标系Xb、Yb、Zb轴的移动量为 xp、yp、zp,欧拉角分别是ψ、θ和φ,则有如下关系:
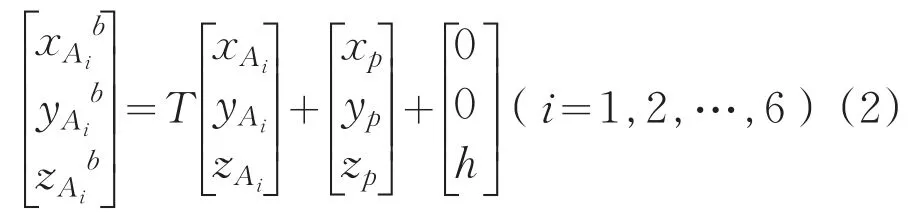
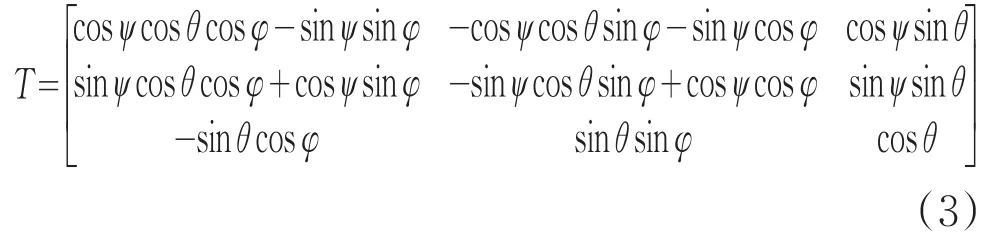
根据A1~A6在运动平台坐标系的分布可以求出根据式(2)可以求出 A1~ A6在基座平台坐标系下的,根据式(1)可以求出B1~B6在基座平台坐标系下的坐标,各支链长度l'及与原始长度相比的变化量Δl为:
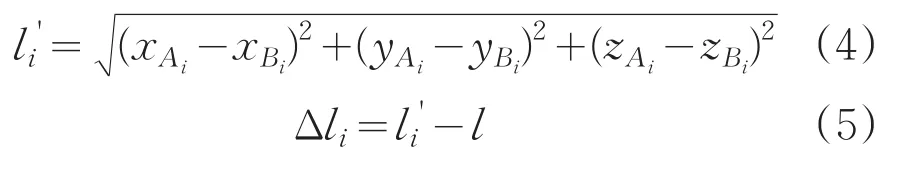
3.2 微动并联机器人工作空间求解
利用柱坐标系的方式构造扫描空间,在高度上以微小步长将搜索空间分割为若干个平行的扫面平面,在每个扫面平面上以极坐标的方式,使运动平台中心点坐标的极径和极角分别从0开始逐渐增大,通过式(4)得到每个扫描点对应位置的6个柔性支链长度l',然后根据约束条件判断是否仍在工作空间范围内,若超出的话记录边界点,依次搜索出各个扫描截面上的边界曲线,进而得到整个工作空间。搜索示意图如图7所示。

图7 工作空间边界搜索示意图
利用上述方法对本文中实际研制的微动并联机器人的工作空间进行分析,结构参数如表2所示,l'的变化范围为l-0.18mm≤li'≤l+0.18mm,即工作空间边界点的判断依据。
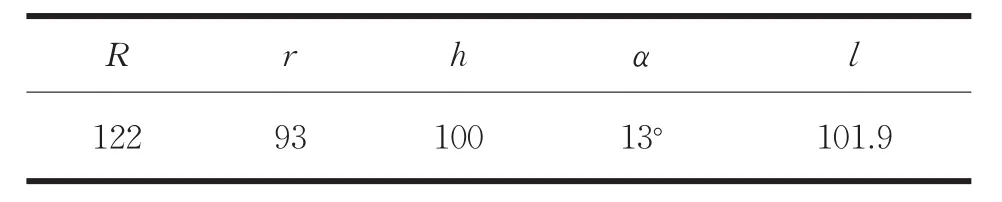
表2 微动并联机器人结构参数mm
首先令三个欧拉角均为零,得到定姿态工作空间如图8所示。
章动角θ即运动平台的灵活姿态角[8],代表了运动平台在任意方向都能够偏转到的角度值,可以评判机构运动平台的倾斜调整能力。为了限制运动平台自身的转动,令ψ=-φ,在每个扫面点添加灵活姿态角判断的扫描,即令ψ从0°到360°进行姿态扫描。得到灵活姿态角为700μrad的工作空间如图9所示。
从图8和图9可以得到:
(1)定姿态工作空间和灵活姿态角为700μrad的工作空间均为较规则的十二面体,侧视投影近似菱形,运动平台处在原点高度时,XY方向调整能力最大,随着高度的上下变化,XY向调整范围逐渐变小。
(2)X向调整范围最大,其次是Y向,Z向调整范围最小。随着灵活姿态角的增大,工作空间逐渐变小。

图8 定姿态工作空间

图9 灵活姿态角θ为700μrad的工作空间
(3)从图9可以得到,运动平台原点在长宽均为0.2mm,高度为0.18mm的长方体中的任一点均可实现任意方向700μrad的倾斜调整,即机器人在X、Y向具有±100μm的调整范围,Z向具有±90μm调整范围,并且在此空间内任意点均可实现任意方向700μrad的倾斜调整。
4 结论
对实际研制的微动并联机器人的工作空间进行了分析。首先针对微动并联机器人的结构特点,分析了影响其工作空间的约束条件。为了获得机器人带有一定倾斜调整能力的工作空间,采用更加直观的欧拉角描述运动平台的姿态,对机器人的运动学逆解的进行求解,并通过给出的空间扫描边界点的方法获得了定姿态工作空间和灵活姿态角工作空间。分析结构表明机器人在给定任意方向具有700μrad的倾斜调整的前提下,在X、Y向具有±100μm的调整范围,Z向具有±90μm调整范围。该分析方法对微动并联机器人设计及性能评价具有重要指导意义。
[1]陈学生,陈在礼,孔民秀.并联机器人研究的进展与现状[J].机器人,2002,24(5):464-470.
[2]黄真.并联机器人及其机构学理论[J].燕山大学学报,1998,20(1):13-17.
[3]冯志友,李永刚,张策,等.并联机器人机构运动与动力分析研究现状及展望[J].中国机械工程,2006,17(9):979-984.
[4]Gosselin.Determination of the workspace of 6-DOF parallel manipulators[J].ASME J Mech Des,1990,112(3):331-336.
[5]许意华,刘德忠,费仁元.3-PTT并联微操作机器人工作空间分析[J].机械科学与技术,2003,22(1):102-104.
[6]张顺心,范顺成,肖汾阳.并联机床主运动机构工作空间分析[J].机械设计,2003,20(3):39-42.
[7]王永,姚太克,周烽,等.望远镜副镜的三自由度并联支撑构型研究与运动分析[J].光学精密工程,2013,21(11):2860-2869.
[8]冯海兵.一种并联宏/微驱动操作手的工作空间[J].光学 精密工程,2013,21(3):717-723.

